1 Дослідження часових та частотних характеристик типових динамічних ланок лінійних сау

1.1 Мета роботи

Метою роботи є дослідження впливу параметрів типових динамічних ланок на їх часові та частотні характеристики та набуття навичок визначення параметрів динамічних ланок за експериментальними графіками.

1.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до лабораторної роботи студенти повинні повторити відповідний лекційний матеріал і дані практичних занять, ознайомитися з матеріалами, що наведено у літературі [3-9], а саме: опис САУ за допомогою диференційних рівнянь; перетворення Лапласа; передавальні функції САУ; часові та частотні характеристики САУ; типові динамічні ланки та їх характеристики.

Програмою досліджень лабораторної роботи є:

– отримання часових та частотних характеристик таких типових динамічних ланок: ідеальної інтегруючої, аперіодичної ланки першого порядку, реальної інтегруючої, реальної диференціюючої, коливальної ланки, аперіодичної ланки другого порядку, консервативної ланки;

– вивчення залежності отриманих характеристик від параметрів динамічних ланок – коефіцієнтів підсилення та постійної часу;

– розрахунок коефіцієнтів динамічних ланок за експериментальними графіками часових та частотних характеристик.

Для виконання роботи студенти повинні знати передавальні функції типових динамічних ланок, приклади технічних пристроїв, які можна описати за допомогою цих ланок, і вміти розраховувати часові та частотні функції ланок за відомою передавальною функцією.

Під динамічною ланкою слід розуміти пристрій будь-якого фізичного вигляду, який описується певним диференційним рівнянням. Класифікація ланок відбувається за виглядом диференційного рівняння.

Застосувавши до диференційного рівняння ланки перетворення Лапласа та взявши відношення зображення вихідної величини до зображення вхідної при нульових початкових умовах, отримаємо передавальну функцію ланки W(s). Передавальна функція, як і диференційне рівняння, описує динамічні властивості ланки і застосовується для опису та оцінки властивостей лінійних систем автоматичного керування.

Для опису динамічних властивостей ланок широко використовують також часові та частотні характеристики.

Часовою характеристикою називають зміну у часі вихідної величини ланки (реакція ланки), яка викликана еталонним вхідним впливом.

Перехідною функцією називають функцію , що описує реакцію ланки на одиничний ступінчастий вплив при нульових початкових умовах.

Функцією ваги, або імпульсною перехідною функцією, називають функцію , що описує реакцію ланки на імпульсний вплив типу δ(t) функції.

Функції , та пов'язані співвідношеннями:

; . (1.1)

У таблиці 1.1 наведено диференційні рівняння, які описують досліджувані ланки та їх передавальні функції. У таблиці прийнято такі позначення: – коефіцієнт підсилення ланки, – постійна часу ланки, – коефіцієнт демпфірування.

Прикладом ідеальної інтегруючої ланки може бути двигун постійного струму, що працює вхолосту, у якого вхідним сигналом є напруга на якорі, а вихідною – кут повороту вала двигуна; інтегруючий операційний підсилювач у режимі інтегрування та ін.

Прикладом аперіодичної ланки першого порядку можуть бути: електродвигун постійного струму, у якого вхідна величина – напруга, що подається на якірну обмотку, а вихідна – кутова швидкість обертання якоря; інерційні датчики; магнітний підсилювач; термостати та інші пристрої.

Прикладом реальної інтегруючої ланки може бути поршневий гідравлічний виконуючий двигун, у якого вхідною величиною є кількість рідини, що потрапляє до циліндра, а вихідною – переміщення поршня.

Прикладом реальної диференціюючої ланки є диференціюючий трансформатор.

Прикладами коливальної ланки можуть бути коливальні RLC-ланцюги, гіроскопічні елементи та ін.

Прикладом аперіодичної ланки другого порядку може бути двигун постійного струму, у якого вхідна величина – напруга на якорі, а вихідна швидкість двигуна.

Таблиця 1.1 – Характеристики досліджуваних ланок

Номер	Найменування ланки	Диференційне рівняння	Передавальна функція
1	Ідеальна інтегруюча
2	Аперіодична першого порядку
3	Реальна інтегруюча
4	Реальна диференціююча
5	Коливальна		, причому
6	Аперіодична другого порядку		, причому
7	Консервативна ланка		()

Консервативна ланка є ідеалізованим випадком, коли можна знехтувати впливом розсіювання енергії у ланці. Прикладом такої ланки можуть бути каскадні магнітні підсилювачі, електромеханічні підсилювачі поперечного поля та ін. Перехідна характеристика ланки має автоколи­вальний характер. Амплітуда коливань дорівнює 2k.

У таблиці 1.2 наведено часові функції досліджуваних ланок та їх передавальні функції. У таблиці прийнято такі позначення: – коефіцієнт підсилення ланки, – постійна часу ланки, – коефіцієнт демпфірування.

Якщо на вхід лінійної САУ подати гармонічну дію, то на її виході встановиться гармонічний процес з амплітудою b і фазою, яка зсунена відносно фази вхідного сигналу на кут (рис. 1.1). Амплітуда і фаза на виході за інших рівних умов залежатимуть від частоти збудження. За цими характеристиками можна судити про динамічні властивості не тільки ланок, а й складних замкнутих САУ.

До частотних характеристик належить комплексна частотна передавальна функція (ЧПФ) , яку отримують, замінивши на у передавальній функції у перетвореннях Лапласа.

Таблиця 1.2 – Часові функції досліджуваних ланок

Номер	Найменування ланки	Перехідна функція	Імпульсна перехідна функція
1	Ідеальна інтегруюча
2	Аперіодична першого порядку
3	Реальна інтегруюча
4	Реальна диференціююча
5	Коливальна	де , , .
6	Аперіодична другого порядку	де
7	Консервативна ланка

а) б)

Рисунок 1.1 – Лінійна неперервна САУ при гармонічній дії: а) схематичне зображення САУ; б) графіки вхідного та вихідного сигналів САУ

Частотна передавальна функція є комплексною функцією від змінної . Її, як і будь-яке комплексне число, можна записати в алгебраїчній та показовій формах:

, (1.2)

де – дійсна частина частотної передавальної функції, яка називається дійсною частотною функцією (ДЧФ);

– уявна частина частотної передавальної функції, яка називається уявною частотною функцією (УЧФ);

– модуль частотної передавальної функції, який називається амплітудною частотною функцією (АЧФ);

– аргумент частотної передавальної функції, який називають фазовою частотною функцією (ФЧФ).

На комплексній площині частотну передавальну функцію визначає вектор ОС, довжина (модуль) якого дорівнює , а кут, утворений цим вектором з дійсною додатною піввіссю, дорівнює . Крива, яку описує кінець цього вектора під час зміни частоти від 0 до нескінченності (годограф вектора ), називається амплітудно-фазовою частотною характеристикою (АФЧХ).

Для визначення модуля та фази частотної передавальної функції на заданій частоті слід відповідну точку годографа з’єднати прямою з початком координат. Довжина отриманого відрізка відповідає у визначеному масштабі модулю, а фаза визначається кутом, утвореним цією прямою та додатною піввіссю дійсних величин (рис. 1.2).

Рисунок 1.2 – Амплітудно-фазова частотна характеристика

Дійсну частотну функцію розраховують так:

. (1.3)

Уявну частотну функцію можливо визначити так:

. (1.4)

АЧФ визначається відношенням амплітуди вихідного сигналу до амплітуди вхідного гармонічного сигналу в усталеному режимі:

. (1.5)

АЧФ визначається як модуль частотної передавальної функції:

(1.6)

Амплітудно-частотна характеристика (АЧХ) показує, як пропускає ланка сигнали різних частот. Оцінювання пропускання здійснюють відносно амплітуд вихідної та вхідної величин.

ФЧФ визначається зсувом фази вихідного сигналу . ФЧФ визначається як аргумент частотної передавальної функції:

, (1.7)

(1.8)

Фазочастотна характеристика (ФЧХ) показує фазові зсуви, які вносить ланка на різних частотах. Оцінювання пропускання здійснюють відносно амплітуд вихідної та вхідної величин.

Окрім перерахованих частотних характеристик (АФЧХ, АЧХ, ФЧХ, ДЧХ, УЧХ), під час аналізу та синтезу САУ широко застосовуються також логарифмічні частотні характеристики (ЛЧХ): логарифмічна амплітудна частотна характеристика (ЛАЧХ); логарифмічна фазова частотна характеристика (ЛФЧХ). ЛЧХ мають переваги перед звичайними АЧХ та ФЧХ, оскільки вони більш наочні та прості у побудові.

Логарифмічною амплітудною частотною характеристикою САУ називають АЧХ цієї системи, виражену в децибелах та побудовану у логарифмічному масштабі частот. ЛАЧХ визначають так:

. (1.9)

Логарифмічною фазовою частотною характеристикою САУ називають залежність фази , виражену у градусах або радіанах, від частоти в логарифмічному масштабі.

ЛЧХ – це ті самі частотні характеристики системи, але побудовані в іншій системі координат. Це найбільш зручна форма представлення частотних характеристик для вирішення задач аналізу і синтезу систем. По осі абсцис відкладають частоту у логарифмічному масштабі, що дозволяє відкласти на заданому відрізку значний діапазон частот. Одиницею вимірювання є декада – інтервал, на якому частота змінюється у десять разів. По осі ординат значення відкладають у децибелах (дБ), а значення – у градусах або радіанах.

В таблицях 1.3 та 1.4 наведені частотні функції досліджуваних ланок.

Таблиця 1.3 – Дійсна та уявна частотні функції досліджуваних ланок

Номер	Наймену- вання ланки
1	Ідеальна інтегруюча
2	Аперіодична першого порядку
3	Реальна інтегруюча
4	Реальна диферен- ціююча
5	Коливальна
6	Аперіодична другого порядку
7	Консерва- тивна ланка

Таблиця 1.4 – Амплітудна та фазова частотні функції досліджуваних ланок

Номер	Наймену- вання ланки
1	Ідеальна інтегруюча
2	Аперіодична першого порядку
3	Реальна інтегруюча
4	Реальна диферент- ціююча
5	Коливальна
6	Аперіодична другого порядку	де
7	Консерва- тивна ланка

1.3 Опис лабораторної установки

Лабораторна робота виконується у середовищі Matlab за допомогою пакету моделювання динамічних систем Simulink.

До складу системи Matlab 6.0 входить пакет моделювання динамічних систем – Simulink 4.0. Це нова, істотно допрацьована версія популярного пакету, який вже довгий час вважається одним із кращих пакетів моделювання динамічних систем, що задаються за допомогою блоків. Пакет Simulink є ядром інтерактивного програмного комплексу, призначеного для математичного моделювання лінійних і нелінійних динамічних систем та пристроїв, представлених своєю функціональною блок-схемою, іменованою s-моделлю або просто моделлю. При цьому можливі різні варіанти моделювання: у часовій області, у частотній області, з подієвим управлінням, на основі спектральних перетворень Фур'є, з використанням методу Монте-Карло (реакція на дії випадкового характеру) і т.ін.

1.4 Порядок виконання роботи і методичні вказівки з її виконання

1.4.1 Запуск програми Simulink

Для запуску програми необхідно заздалегідь запустити пакет MATLAB. Після відкриття основного вікна програми MATLAB потрібно запустити програму Simulink одним із двох способів:

– натиском кнопки (Simulink) на панелі інструментів командного вікна MATLAB;

– у командному рядку головного вікна MATLAB набрати команду Simulink і натиснути клавішу Enter на клавіатурі.

Після виклику Simulink відкривається вікно оглядача розділів бібліотеки Simulink (рис. 1.3).

Бібліотека Simulink містить такі основні розділи: Continuous – лінійні блоки, Discrete – дискретні блоки, Functions & Tables – функції і таблиці, Math – блоки математичних операцій, Nonlinear – нелінійні блоки, Signals & Systems – сигнали і системи, Sinks – реєструючі пристрої, Sources – джерела сигналів і дій, Subsystems – блоки підсистем.

Рисунок 1.3 – Вікно оглядача розділів бібліотеки Simulink

Під час вибору відповідного розділу бібліотеки у правій частині вікна відображується його вміст.

1.4.2 Створення моделі

Для створення моделі у середовищі Simulink необхідно послідовно виконати ряд дій.

Створити новий файл моделі за допомогою команди File/New/Model, або використовуючи кнопку на панелі інструментів (тут і далі, за допомогою символу «/» вказано пункти меню програми, які необхідно послідовно вибрати для виконання вказаної дії).

Розташувати блоки у вікні моделі. Для цього слід відкрити відповідний розділ бібліотеки (наприклад Sources – Джерела). Далі, вказавши курсором на необхідний блок і натиснувши на ліву клавішу миші – «перетягнути» блок у вікно створення моделі. Для видалення блоку необхідно вибрати його і натиснути клавішу Delete на клавіатурі.

Зібрати стенд для дослідження перехідних характеристик (рис. 1.4) та провести моделювання.

Рисунок 1.4 – Стенд для дослідження перехідних характеристик аперіодичної ланки першого порядку

Для побудови стенду використовують такі блоки:

• блок Step (з бібліотеки simulink/Sources);

• блок TransferFunction (з бібліотеки simulink/Continuous);

• блок Mux (з бібліотеки simulink/SignalRouting);

• блок Scope (з бібліотеки simulink /Sinks).

Якщо потрібно змінити параметри блоку, встановлені програмою «За умовчанням», необхідно двічі натиснути лівою клавішею миші, вказавши курсором на зображення блоку, у вікні редагування параметрів даного блоку внести відповідні зміни. Під час задання чисельних параметрів слід мати на увазі, що у якості десяткового роздільника використовується крапка, а не кома. Після внесення змін потрібно закрити вікно, натиснувши кнопку «OK».

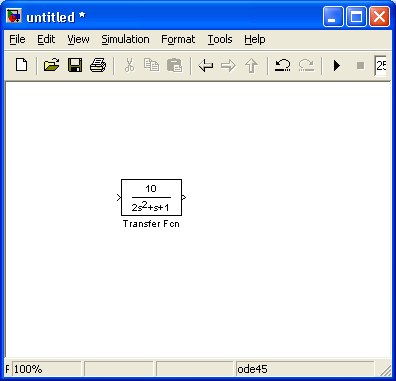
Блок передавальної функції Transfer Fcn задає передавальну функцію у вигляді відношення поліномів

,

де nn і nd – порядок чисельника і знаменника передавальної функції, num – вектор або матриця коефіцієнтів чисельника, den – вектор коефіцієнтів знаменника.

Параметри блоку містять (рис. 1.5):

• Numerator – вектор або матрицю коефіцієнтів полінома чисельника;

• Denominator – вектор коефіцієнтів полінома знаменника;

• Absolute tolerance – абсолютну погрішність.

а) б)

Рисунок 1.5 – Блок, що моделює передавальну функцію (а) і вікно редагування параметрів блоку (б)

Так, для розташування аперіодичної ланки у моделі, необхідно в бібліотеці Continuous обрати блок Transfer Fcn, винести його в область моделі та змінити параметри блоку відповідно до варіанту завдання (Додаток А).

Слід розташувати генератор ступінчастого сигналу Step (бібліотека Sources), змінивши параметр блоку Step time – час настання перепаду сигналу на «0».

Для перегляду графіків досліджуваних сигналів потрібно на полі моделі розташувати блок осцилографу Scope (бібліотека Sinks).

Після розташування на схемі всіх блоків слід з'єднати елементи схем. З’єднання блоків відповідно до структури моделі необхідно проводити від вихідного порту блоку до вхідного порту (рис. 1.6) із натиснутою лівою клавішею миші, після чого відпустити клавішу. У разі правильного з'єднання зображення стрілки на вході блоку змінює колір. Для створення вузла потрібно виділити відповідну лінію з’єднання і, натиснувши Ctrl на клавіатурі та праву клавішу миші, протягнути лінію до входу потрібного блоку.

Рисунок 1.6 – З’єднання блоків

Після того як макет побудовано, необхідно провести моделювання. Для запуску процесу моделювання потрібно натиснути кнопку Start Simulation на панелі інструментів вікна побудови моделі. Після подвійного натискання на блоці осцилографа відкриється вікно для перегляду вихідного сигналу (рис. 1.7).

Налаштування вікна осцилографа виконується за допомогою панелей інструментів. Для відображення графіка в автомасштабі необхідно натиснути на панелі інструментів кнопку (Autoscale) – автоматична установка масштабів на обох осях.

Рисунок 1.7 – Вікно осцилографа з графіком перехідної характеристики

1.4.3 Побудова перехідних і частотних характеристик САУ

Виконується за допомогою інструменту Simulink LTI-Viewer. Насамперед необхідно вказати точки перегляду на вході (Input Point) та виході (Output Point) досліджуваної системи, для чого виділити лінію на вході/виході досліджуваної системи та натиснути праву кнопку миші, де у меню обрати Linearization Points–>Input Point або Output Point відповідно.

Після виконання команди у панелі вікна моделі

Tools/Control Design/Linear Analysis...

відкриється вікно аналізу (рис. 1.8).

Для переходу до LTI-Viewer необхідно натиснути кнопку Linearize Model. На екрані з’явиться вікно з графіками перехідної характеристики. Для відображення інших характеристик необхідно натиснути праву клавішу миші (рис. 1.9) та обрати зі списку необхідну характеристику. Так, step – графік перехідної характеристики, impulse – графік імпульсної характеристики, bode – ЛАЧХ та ЛФЧХ, Nyquist – графік АФЧХ системи.

1.4.4 Дослідити типові динамічні ланки за різних значень параметрів, використовуючи наведену методику. Побудувати віртуальні макети для дослідження часових та частотних характеристик типових динамічних ланок із параметрами, що задано у завданні (Додаток А). Провести моделювання та проаналізувати результати.

Рисунок 1.8 – Вікно аналізу моделі САУ

Рисунок 1.9 – Вікно графічного інтерфейсу LTI Viewer

1.5 Зміст звіту

Загальні правила оформлення матеріалів звіту наведено у вступі до методичних вказівок.

У теоретичній частині потрібно:

– навести рівняння, що описують досліджені динамічні ланки з конкретними величинами коефіцієнтів;

– навести передавальні функції динамічних ланок;

– вивести аналітичні вирази часових та частотних характеристик за завданням викладача.

В експериментальній частині навести часові та частотні характеристики досліджених ланок при різних значеннях параметрів, зображуючи однойменні характеристики для кожної окремої ланки при різних значеннях параметрів на одному графіку. Розрахувати значення параметрів ланки (коефіцієнта підсилення та постійної часу) за отриманими характеристиками.

У висновках проаналізувати, як впливає значення параметрів ланки на вид часових та частотних характеристик.

1.6 Контрольні запитання і завдання

1. Назвіть класифікація систем автоматичного управління.

2. Назвіть типові динамічні ланки САУ, їх характеристики.

3. Вкажіть передаточні функції типових динамічних ланок.

4. Опишіть перехідні та імпульсні характеристики типових динамічних ланок.

5. Як за виглядом передавальної функції системи знайти її перехідну характеристику?

6. Опишіть знаходження передаточних функцій динамічних ланок за експериментальним графіком перехідного процесу.

7. Який фізичний зміст амплітудно-частотної та фазочастотної характеристик САУ?

8. Викладіть методику побудови логарифмічних частотних та амплітудно-фазових характеристик САУ.

9. У чому перевага логарифмічних частотних характеристик?

10. Наведіть частотні характеристики типових динамічних ланок.