2.3.2 Определение количества тарелок
По известным коэффициентам массоотдачи найдём частные числа единиц переноса:
а) Для верхней части колонны:
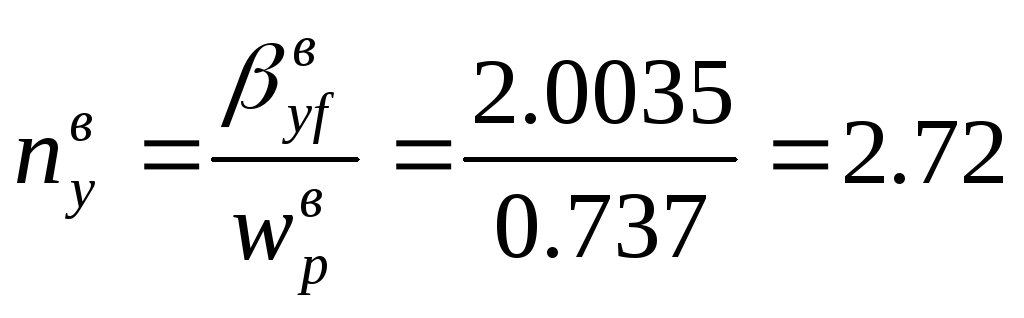
б) Для нижней части колонны:
Найдём общее число единиц переноса по формуле:
,
где
и
-число
единиц переноса по паровой и жидким
фазам на тарелке;
и
-тангенсы
угла наклона соответственно равновесной
и рабочей линий.
Тангенсы угла наклона рабочих линий найдём, продифференцировав их по аргументу, получим:
а) Для верхней части колонны:
б) Для нижней части колонны:
Тангенсы угла наклона равновесной линии найдём с помощью ПК см. Прил. II:
а) Для верхней части колонны:
б) Для нижней части колонны:
Тогда число общих единиц переноса равно:
а) Для верхней части колонны:
б) Для нижней части колонны:
Определим локальную эффективность тарелки по формуле:
а) Для верхней части колонны:
б) Для нижней части колонны:
Для построения кинетической кривой воспользуемся вычислительной средой MathCAD и определим количество реальных тарелок.
а) Для верхней части колонны:
б) Для нижней части колонны:
2.3.3 Расчёт высоты
Общая высота
колонны включает высоту её тарельчатой
части
и определяется по формуле:
,
где
- высота тарельчатой части колонны,
;
и
-расстояние
между верхней тарелкой и крышкой колонны
и между днищем колонны и нижней тарелкой,
.
Расстояния
и
для колонн диаметром
равны:
и
.
Высота колонны получается равной:
2.3.4 Расчёт гидравлического сопротивления колонны
Гидравлическое сопротивление колонны равно:
2.4 Тепловой расчет установки
2.4.1 Тепловой баланс
Количество теплоты, выделяющееся при конденсации паров дистиллята, находим по уравнению:
,
где
-удельная
теплота испарения дистиллята,
;
-флегмовое
число;
-массовый
расход дистиллята.
Удельную теплоту испарения найдём по формуле:
Зная мольный состав
дистиллята, исходной смеси и кубового
остатка, по диаграмме
найдём их температуры кипения:
Зная мольный состав и температуру кипения дистиллята, найдём удельную теплоту испарения:
Количество теплоты, отдаваемое дистиллятом при охлаждении, находим по формуле:
,
где
-температура
кипения дистиллята;
-теплоёмкость
дистиллята при температуре кипения.
Количество теплоты, получаемое исходной смесью, в паровом подогревателе найдём по формуле:
Количество теплоты, отдаваемое кубовым остатком в водяном холодильнике, найдём по формуле:
Найдём количество тепла, которое необходимо подвести в куб-испаритель по формуле:
Найдём расход пара в куб-испаритель.
По известному
абсолютному давлению греющего пара (
)
найдём его теплоту конденсации:
Массовый расход пара равен:
2.4.2 Подробный расчет холодильника кубового остатка
Температурная схема:
,
ректификация бинарный смесь жидкость
Тогда
.
По известному составу и средней
температуре найдём необходимые параметры
теплоносителя и хладагента:
а) Удельная теплоемкость кубового остатка:
б) Количество теплоты:
в) Теплоемкость воды:
г) Расход воды:
Для определения ориентировочной площади теплообмена примем коэффициент теплопередачи
Определим ориентировочно площадь теплообмена:
Для обеспечения
интенсивного теплообмена попытаемся
подобрать аппарат с турбулентным или
переходным режимом течения теплоносителей.
Возьмём теплообменный аппарат типа
“труба в трубе” по ГОСТ (9830-79) с диаметром
кожуховой трубы
и теплообменной
кубовый остаток направим в кожуховую
трубу, а охлаждающую воду в теплообменную
трубу.
Зададимся критерием Рейнольдса для кубового остатка : Re2=10000
Эквивалентный диаметр кольцевого сечения: dэкв=0.011
Вязкость кубового
остатка при его средней температуре
:
Плотность кубового
остатка при его средней температуре
:
Найдем скорость кубового остатка:
Найдем площадь поперечного сечения:
Найдем по каталогу стандартную площадь:
Найдем по стандартной площади скорость и число Рейнольдса:
В теплообменной трубе хладагент- вода.
Зададимся критерием Рейнольдса для воды : Re1=10000
Эквивалентный диаметр кольцевого сечения: dэкв=0.03 м
Вязкость(Пас) воды
при ее средней температуре
:
Плотность(кг/м3)
воды при ее средней температуре
:
Найдем скорость воды:
Найдем площадь поперечного сечения:
Найдем по каталогу стандартную площадь:
Найдем по стандартной площади скорость и число Рейнольдса:
Температуры стенки со сторон холодного и горячего теплоносителей будем искать с помощью метода итераций. Суть метода заключается в нахождении удельного потока теплоты со стороны хладагента и теплоносителя как функций от температуры одной из стенок теплообменника и решения уравнения графическим методом или с помощью ПК относительно температуры стенки.
Сначала рассмотрим холодный теплоноситель – воду. Найдем для нее теплофизические свойства и при ее средней температуре:
Теплопроводность:
Теплоемкость (Дж/кгК):
Вязкость (Пас):
=7.482*10-4
Плотность (кг/м3):
Определим критерий Прандтля для кубового остатка по формуле:
.
Зададимся температурой стенки со стороны хладагента tстхол=37,115
Найдем теплофизические параметры и критерий Прандтля при температуре стенки хладагента:
Теплопроводность:
Теплоемкость (Дж/кгК):
Вязкость (Пас):
=6,899
10-4
Представим критерий Прандтля при температуре стенки как функцию от этой температуры, это позволяют сделать функциональные зависимости теплофизических свойств компонентов смеси от температуры:
Так как режим течения жидкости турбулентный, то критерий Нуссельта для водыбудем находить по формуле:
Выразим коэффициент теплоотдачи как функцию от температуры соответствующей стенки:
,
Зная коэффициенты теплоотдачи можно выразить удельный тепловой поток как функцию от температуры соответствующей стенки:
Выразим температуру
горячей стенки (
)
как функцию от температуры холодной
стенки (
).
Это позволяет сделать соотношение:
Коэффициент
теплопроводности стали, берём из [3]
,
среднее значение тепловой проводимости
загрязнений стенок берём из [3] для смеси
паров бензол - толуол и воды среднего
качества
.
Решив уравнение,
находим
.
Теперь рассмотрим горячий теплоноситель – кубовый остаток. Найдем его теплофизические свойства при его средней температуре.
Теплопроводность:
Теплоемкость (Дж/кгК):
Определим критерий Прандтля для кубового остатка по формуле:
.
Найдем теплофизические
параметры и критерий Прандтля при
температуре стенки горячего теплоносителя
(
):
Вязкость
Теплопроводность
Теплоемкость
Представим критерий Прандтля при температуре стенки как функцию от этой температуры, это позволяют сделать функциональные зависимости теплофизических свойств компонентов смеси от температуры:
Так как режим течения жидкости можно считать турбулентным, то критерий Нуссельта для кубового остатка будем находить по формуле (для кубового остатка):
Выразим коэффициент теплоотдачи как функцию от температуры соответствующей стенки:
,
Зная коэффициенты теплоотдачи можно выразить удельный тепловой поток как функцию от температуры соответствующей стенки:
Потоки равны с
погрешностью
Найдём коэффициент теплопередачи:
Расчетная площадь поверхности теплопередачи:
Теплообменник обладает следующими характеристиками: