
- •1. Основные понятия
- •2. Виды интегрируемых нелинейных уравнений п-го порядка
- •2.1. Дифференциальное уравнение вида
- •2.2. Дифференциальное уравнение вида
- •2.3. Дифференциальные уравнения вида
- •2.4. Уравнения, левая часть которого есть точная производная
- •Задания для самостоятельной работы
- •3. Уравнения п-го порядка, допускающие понижения порядка.
- •3.1. Уравнения вида
- •3.2. Уравнение вида
- •3.3. Уравнение, однородное относительно искомой функции и ее производных
- •3.4. Обобщенно однородное дифференциальное уравнение вида
- •3.5. Уравнения, приводимые к виду
- •4.1.2. Неоднородное линейное уравнение
- •4.2. Линейные дифференциальные уравнения с постоянными коэффициентами
- •4.2.1. Однородное уравнение
- •Алгоритм нахождения общего решения однородного линейного уравнения с постоянными коэффициентами
- •4.2.2. Неоднородные линейные уравнения
- •Алгоритм нахождения частного решения уравнения п-го порядка с постоянными коэффициентами методом вариации произвольных постоянных (метод Лагранжа)
- •Алгоритм нахождения частного решения неоднородного линейного уравнения с постоянными коэффициентами методом неопределенных коэффициентов
- •Задания для самостоятельной работы
- •4.3. Линейные дифференциальные уравнения с переменными коэффициентами
- •4.3.1. Уравнения Эйлера
- •Задания для самостоятельной работы
- •4.4. Дифференциальные уравнения второго порядка
- •4.4.1. Приведение уравнения 2-го порядка к каноническому виду
- •4.4.2. Метод исключения из уравнения 2-го порядка слагаемого, содержащего первую производную искомой функции. Уравнение Чебышева
- •Задания для самостоятельной работы
- •4.4.3. Приведение уравнения 2-го порядка к самосопряженному виду
- •4.4.4. Краевая задача для уравнения 2-го порядка
- •Задачи для самостоятельной работы
- •Решение уравнений второго порядка с помощью рядов
- •Задачи для самостоятельной работы
- •Метод малого параметра.
- •Задания для самостоятельной работы
- •Контрольные работы
- •Ответы к заданиям для самостоятельной работы
- •Список использованных источников
Задания для самостоятельной работы
Проинтегрировать уравнения и, где указано, найти решения, удовлетворяющие начальным условиям.
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
5.
.
5.
![]() .
.
-
 .
7.
.
7.
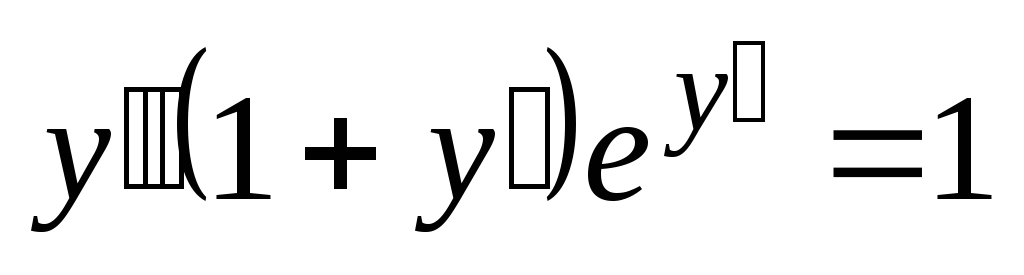 .
8.
.
8.
 .
.
9.
![]() .
10.
.
10.
![]() .
.
3. Уравнения п-го порядка, допускающие понижения порядка.
3.1. Уравнения вида
Если дифференциальное уравнение имеет вид
![]() ,
,
то его порядок можно понизить с помощью подстановки
![]() .
.
Действительно, тогда получим уравнение
![]() ,
,
порядок которого на k единиц меньше исходного уравнения.
Пример 13.
Найти решение уравнения:
![]() .
.
▲ Сделаем замену
, и
вычислим EMBED Equation.3
![]() тогда исходное уравнения будет иметь
вид:
тогда исходное уравнения будет иметь
вид:
![]() .
.
Это уравнение первого порядка с разделяющимися переменными
![]() ,
,
интегрируя его, находим
![]() ,
,
откуда
![]() или
или
![]() .
.
Далее дважды интегрируем последнее уравнение, получаем:
![]() .▲
.▲
3.2. Уравнение вида
Порядок дифференциального уравнения вида
![]() (22)
(22)
может быть понижен,
если ввести замену
![]() ,
где
,
где
![]() -
новая неизвестная функция, а переменная
у является аргументом.
-
новая неизвестная функция, а переменная
у является аргументом.
Вычислим производные

подставляя производные в исходное уравнение (22) мы получаем уравнение (n – 1)-го порядка с искомой функцией р от независимой переменной у.
Принимая у за независимую переменную. Мы могли потерять решение вида y = const. Непосредственной подстановкой y = b в уравнение (22) можно выяснить, имеет ли оно решение такого вида.
Пример 14.
Проинтегрировать уравнение:
![]() .
.
▲ Сделаем замену
![]() и приняв у за новую переменную,
получим
и приняв у за новую переменную,
получим
![]() ,
,
тогда исходное уравнение можно записать в виде:
![]()
Для того чтобы
решить это уравнение предположим, что
![]() ,
тогда
,
тогда
![]() .
.
Следовательно, получаем уравнение
![]() ,
,
которое является неоднородным линейным уравнением 1-го порядка. Для его решения воспользуемся формулой Эйлера:
![]() .
.
Следовательно,
![]() ,
,
откуда находим
![]() .
.
Интегрируя это уравнение, получаем
![]() .
.
Функция у = 0 также будет решением исходного уравнения и притом частным. ▲
3.3. Уравнение, однородное относительно искомой функции и ее производных
Если дифференциальное
уравнение вида
![]() является однородным относительно
искомой функции и ее производных, т.е.
справедливо тождество:
является однородным относительно
искомой функции и ее производных, т.е.
справедливо тождество:
![]() , (23)
, (23)
то порядок уравнения можно понизить на единицу, положив
![]()
Действительно,
последовательно дифференцируя соотношение
![]() ,
имеем:
,
имеем:

где
![]() -
известная функция.
-
известная функция.
Далее, подставив значения производных в уравнение (23) и используя однородность функции F, получаем:
![]() .
.
Правая часть
тождества представляет собой уже
уравнение
![]() -го
порядка. Если мы найдем его общее решение
-го
порядка. Если мы найдем его общее решение
![]() ,
,
то, заменив z
на
![]() ,
получим
,
получим
![]() .
.
Интегрируя это уравнение, имеем
![]() .
.
Это общее решение исходного уравнения (23).
Пример 15. Найти общее решение уравнения:
 .
.
▲ Введем подстановку
![]() и вычислим вторую производную
и вычислим вторую производную
![]() .
.
Подставив в исходное уравнение, получим
![]() ,
,
сократив на
![]() ,
будем иметь:
,
будем иметь:
![]()
![]() ,
или
,
или
![]() .
.
Разделяя переменные и интегрируя это уравнение, получим:
![]() .
.
Далее с учетом
того, что
![]() ,
будем иметь
,
будем иметь
![]() .
.
Интегрируя это уравнение, получим
.
Это общее решение исходного уравнения. ▲
3.4. Обобщенно однородное дифференциальное уравнение вида
Дифференциальное уравнение вида
![]() , (24)
, (24)
называется обобщенно однородным, если функция F удовлетворяет тождеству
Если уравнение (24) обобщенно однородное, то замена переменных
![]() , (25)
, (25)
приводит к уравнению, явно не содержащему независимую переменную t. Следовательно, порядок такого уравнения можно понизить. Вычислим производные
 Подставляя
значения этих производных в уравнение
(24) и пользуясь обобщенной однородностью,
получаем:
Подставляя
значения этих производных в уравнение
(24) и пользуясь обобщенной однородностью,
получаем:

Пример 16.
Найти общее решение уравнения:
![]() .
.
▲ Проверим исходное
уравнение на обобщенную однородность.
С этой целью вместо переменных
![]() подставим в выражение для функции
подставим в выражение для функции
![]() соответственно
соответственно
![]() и, если это возможно, подберем значение
t таким образом, чтобы
выполнялось тождество
и, если это возможно, подберем значение
t таким образом, чтобы
выполнялось тождество
![]() .
.
Очевидно, что это
тождество выполняется при t=1/2
![]() .
Следовательно, исходное уравнение
представляет собой обобщенно однородное
уравнение, и поэтому для его решения
воспользуемся заменой (25)
.
Следовательно, исходное уравнение
представляет собой обобщенно однородное
уравнение, и поэтому для его решения
воспользуемся заменой (25)
![]() .
.
Далее вычислим производные в новых переменных


Подставим значения этих производных, а также х и у в исходное уравнение. После преобразований придем к уравнению:
![]() .
.
Это уравнение явно
не содержит переменную t,
поэтому посредством замены
![]() понизим его порядок на единицу:
понизим его порядок на единицу:
![]() .
.
Проинтегрировав последнее уравнение, находим
![]() ,
т.к.
,
т.к.
![]() ,
то
,
то
![]() .
.
Интегрируя это уравнение, находим
![]() ,
,
откуда
![]() .
.
Таким образом, окончательно получаем решение исходного уравнения в параметрической форме:
 .▲
.▲
