13.5. Прохождение деревьев, леса

Во многих приложениях необходимо пройти лес, заходя в узлы (т.е. обрабатывая их) некоторым систематическим образом. Посещение узла может быть связано с простой операцией, такой как печать содержимого узла, или со сложной, такой как вычисление функции. Единственное, что мы будет предполагать — это то, что при посещении узла структура дерева не меняется.

Основными способами прохождения дерева являются:

• в глубину (сверху вниз);

• в ширину (горизонтальный порядок);

• снизу вверх;

• в симметричном порядке (для бинарных деревьев).

При прохождении в глубину (прохождение в прямом порядке) узлы леса проходятся в соответствии со следующей рекурсивной процедурой:

1. посетить корень первого дерева;

2. пройти в глубину поддеревья первого дерева (если оно есть);

3. пройти в глубину оставшиеся деревья, если они есть.

Например, для леса, показанного на рис. 2.10, узлы будут проходиться в следующем порядке: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S.

Для бинарных деревьев эта процедура упрощается и выглядит следующим образом:

1. посетить корень;

2. пройти в глубину левое поддерево;

3. пройти в глубину правое поддерево.

Заметим, что прохождение леса в глубину в точности такое же, как и прохождение в глубину бинарного дерева, являющегося его представлением. Именно этот факт и делает указанное выше соответствие «естественным».

Прохождение снизу вверх (обратный порядок или концевой порядок) осуществляется согласно следующей рекурсивной процедуре:

1. пройти снизу вверх поддеревья первого дерева, если они есть;

2. посетить корень первого дерева;

3. пройти снизу вверх оставшиеся деревья, если они есть.

При этом порядке прохождения узлы леса рис. 2.10 проходятся в следующем порядке:

B, D, E, F, C, G, J, K, I, L, H, A, O, P, N, R, Q, S, M.

Рекурсивная процедура прохождения снизу вверх применительно к бинарным деревьям имеет следующий вид:

1. пройти снизу вверх левое поддерево;

2. пройти снизу вверх правое поддерево;

3. посетить корень.

F, E, D, K, J, L, I, H, G, C, B, P, O, R, S, Q, N, M, A.

Симметричный порядок для бинарных деревьев определятся рекурсивно следующим образом:

1. пройти в симметричном порядке левое поддерево;

2. посетить корень;

3. пройти в симметричном порядке правое поддерево.

Такой способ прохождения известен как лексикографический порядок или внутренний прядок.

Прохождение дерева снизу вверх эквивалентно прохождению в симметричном порядке бинарного дерева, соответствующего ему.

Последний способ прохождения дерева — горизонтальный порядок или в ширину. При таком способе узлы дерева проходятся слева направо уровень за уровнем от корня вниз. Т.о. узлы леса рис. 13.8 будут проходиться в следующем порядке:

A, M, B, C, G, H, N, Q, S, D, E, F, I, L, O, P, R, J, K.

Примеры:

Прямой порядок: A B D G C E H I F

Симметричный порядок: D G B A H E I C F

Обратный порядок: G D B H I E F C A

Прямой порядок: A B C E I F J D G H K L

Симметричный порядок: E I C F J B G D K H L A

Обратный порядок: I E J F C G K L H D B A

Рис. 13.10. Прохождение бинарных деревьев

Многие алгоритмы и процессы, использующие бинарные деревья, распадаются на 2 фазы. В первой фазе строится бинарное дерево, а во второй оно проходится.

В качестве примера рассмотрим применение бинарного дерева для сортировки чисел. Входной файл содержит список чисел, нужно распечатать числа в возрастающем порядке. По мере того, как мы считываем число, оно помещается в бинарное дерево. Все совпадающие значения также помещаются в дерево. При сравнении числа с содержимым узлов дерева выбирается тот узел, у которого еще не занята правая или левая ветвь, которая в свою очередь выбирается таким образом, что слева записывается меньшее число, чем число в узле, а справа записывается большее число, чем в узле или равное ему. Таким образом, если входной список равен 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5, то будет построено бинарное дерево, показанное на рис. 13.11.

Рис. 13.11. Бинарное дерево, построенное для сортировки

Такое бинарное дерево обладает тем свойством, что содержимое каждого узла в левом поддереве узла n меньше, чем содержимое узла n, а содержимое каждого узла в правом поддереве узла n больше или равно содержимому узла n. Таким образом, если дерево проходится в симметричном порядке (левое поддерево, корень, правое поддерево), то числа печатаются в возрастающем порядке, т.е. 3, 4, 4, 5, 5, 7, 9, 14, 14, 15, 16, 17, 18, 20.

Алгебраическая формула или логическая функция также могут быть представлены бинарным деревом. Например, на рис. 13.12 показано дерево, соответствующее арифметическому выражению a – b (c/d + e/f).

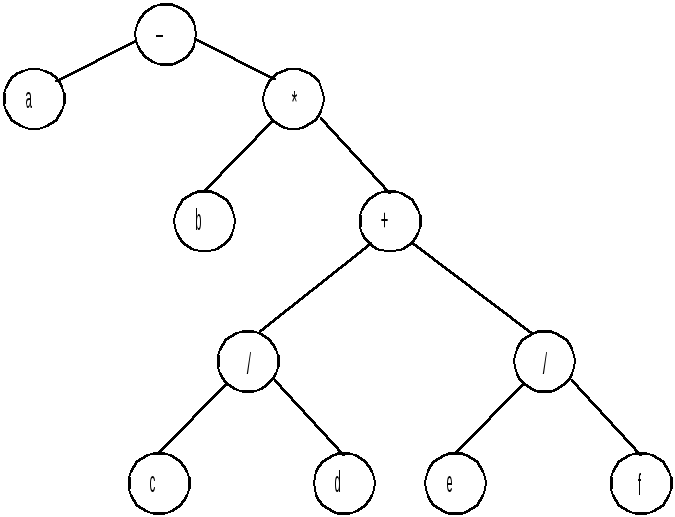
Рис. 13.12. Представление формулы в виде дерева

Используя дерево, легко выполнить переход от инфиксной (обычной) формы записи арифметического выражения (логической функции) к постфиксной (снизу вверх) и к префиксной (сверху вниз).

Например, A+B — инфиксная запись (левое поддерево, корень, правое поддерево);

A B + постфиксная запись (левое поддерево, правое поддерево, корень),

+ A B префиксная запись (корень, левое поддерево, правое поддерево).

Итак, рис. 13.12 позволяет записать

- сверху вниз –a * b + / c d / e f (префиксная запись)

- снизу вверх a b c d / e f / + * – (постфиксная запись)

Такие формы представления позволяют оперировать без скобок, сохраняя правильность выполнения операций.