Раздел 5. Проецирование поверхностей

5.1 Основные понятия и определения

Поверхность – это множество l₁, l₂ … l_i последовательных положений линии l, движение и форма которой подчинены определенному закону. Под законом следует понимать характер, порядок, правила, траекторию перемещения линии l в пространстве таким образом, чтобы в каждом новом положении члены множества l₁, l₂ … l_i касались друг друга, образуя оболочку поверхности.

В формировании поверхности принимают участие подвижные и неподвижные линии. Подвижная линия, участвующая в формировании поверхности, называется образующей; неподвижная линия (или плоскость), относительно которой перемещается образующая (в большинстве случаев пересекая ее), называется направляющей. На рис. 48 представлен порядок формирования цилиндрической (рис. 48а) и конической (рис. 48б) поверхностей. В первом случае образующая перемещается параллельно самой себе, оставаясь в любом положении перпендикулярной горизонтальной плоскости проекций и пересекая расположенную в ней горизонтальную окружность. Во втором случае изменился закон перемещения образующей: в

Рис. 48а

Рис. 48б

любом положении она проходит через одну и ту же точку S, пересекая направляющую окружность. Нетрудно догадаться, что если бы направляющей была не окружность, а многоугольник, то сохраняя вид перемещения образующей, мы бы получили для первого случая призматическую, а для второго – пирамидальную поверхности. И это, опять таки, за счет изменения закона перемещения образующей (не по окружности, а по многоугольнику).

Д искретный каркас поверхности – это конечное множество образующих и направляющих (или точек), задающих поверхность в пространстве и на чертеже. Термин следует понимать буквально, как сетку опорных линий поверхности. На рис. 49 представлены дискретные каркасы сферической поверхности (рис. 49а) и конической поверхности общего вида (рис. 49б). Построение чертежа относительно сложной поверхности сводится к построению проекции ее дискретного каркаса. На рис. 50а представлен чертеж конической поверхности общего вида, дискретный каркас которой показан на рис. 49б. Для простейших поверхностей (сферы, кругового конуса, кругового цилиндра и др.) с явно выраженным законом их образования в построении дискретного каркаса необходимости нет, поскольку каждая из них

Рис. 49а

Рис. 49б

исчерпывающе полно может быть задана проекциями их наружного контура (очерками, рис. 50б).

Рис. 50а

Рис. 50б

С ледует различать термины «очерк» поверхности и «проекция» поверхности. Применительно к термину «очерк» речь идет о проекциях только наружного контура, ограничивающего внешние линии проекции. Для сравнения на рис. 51а дана чертеж пирамиды, а на рис. 51б очерки этой же поверхности. Отметим, что для упомянутых кругового конуса, кругового цилиндра и сферы, не имеющих вырезов, пересечений и т.д., очерки и проекции совпадают (рис. 50б).

Рис. 51а

Рис. 51б

Непрерывный каркас поверхности – это множество l₁, l₂ … l_i последовательных положении линии l, заполняющих поверхность таким образом, что через каждую точку поверхности может быть проведена единственная линия этого множества. В рамках нашего курса термин носит больше теоретический характер, но предоставляет наиважнейший практический тезис: ЧЕРЕЗ ЛЮБУЮ ТОЧКУ ПОВЕРХНОСТИ МОЖЕТ БЫТЬ ПРОВЕДЕНА ЕДИНСТВЕННАЯ ОБРАЗУЮЩАЯ. Именно этот тезис лежит в основе построения недостающих проекций точек на поверхности, предопределяя их единственное положение на каждой из них.

П

Рис. 52а

Рис. 52б

орядок поверхности – это косвенная характеристика ее сложности, численно равная наибольшему количеству точек пересечения прямой с поверхностью. Если принять к сведению, что касание прямой с поверхностью есть частный случай пересечения, то при определении порядка поверхности подобные случаи следует исключать. В этой ситуации становиться очевидным, что, например, сфера, конус, цилиндр являются поверхностями второго порядка (рис. 52а), а, например, тор – поверхностью четвертого порядка (рис. 52б).

Критерием полноты задания поверхности на чертеже является возможность построения недостающих проекций точки на поверхности по одной заданной проекции этой точки. Для построения недостающей проекции точки на поверхности в общем случае необходимо:

• через заданную проекцию точки (1”, рис. 53а) провести проекцию образующей (l”, рис. 53б);

• по закону формирования поверхности простроить недостающую проекцию этой образующей (l’, рис. 53в);

• по линии проекционной связи найти на ней недостающую искомую проекцию этой точки (1’, рис. 53г).

П оскольку на основании формулировки непрерывного каркаса поверхности через любую точку поверхности может быть проведена единственная образующая, полученное решение (положение точки 1’) тоже будет единственным.

Рис. 53а

Рис. 53б

5.2 Классификация поверхностей.

Предварительно заметим, что предлагаемая здесь классификация поверхностей является наипростейшей, занимающей в рамках всех возможных классификационных признаков минимальную часть. Следует также принять к сведению, что в нашем цикле начертательной геометрии раздел «Поверхности» рассматривается не более чем с точки зрения формирования конфигурации

Рис. 53в

Рис. 53г

деталей, имеющих переходы без учета взаимодействия поверхности с окружающей средой.

Рассмотрим классификацию поверхностей по двум классификационным признакам.

В

Рис. 54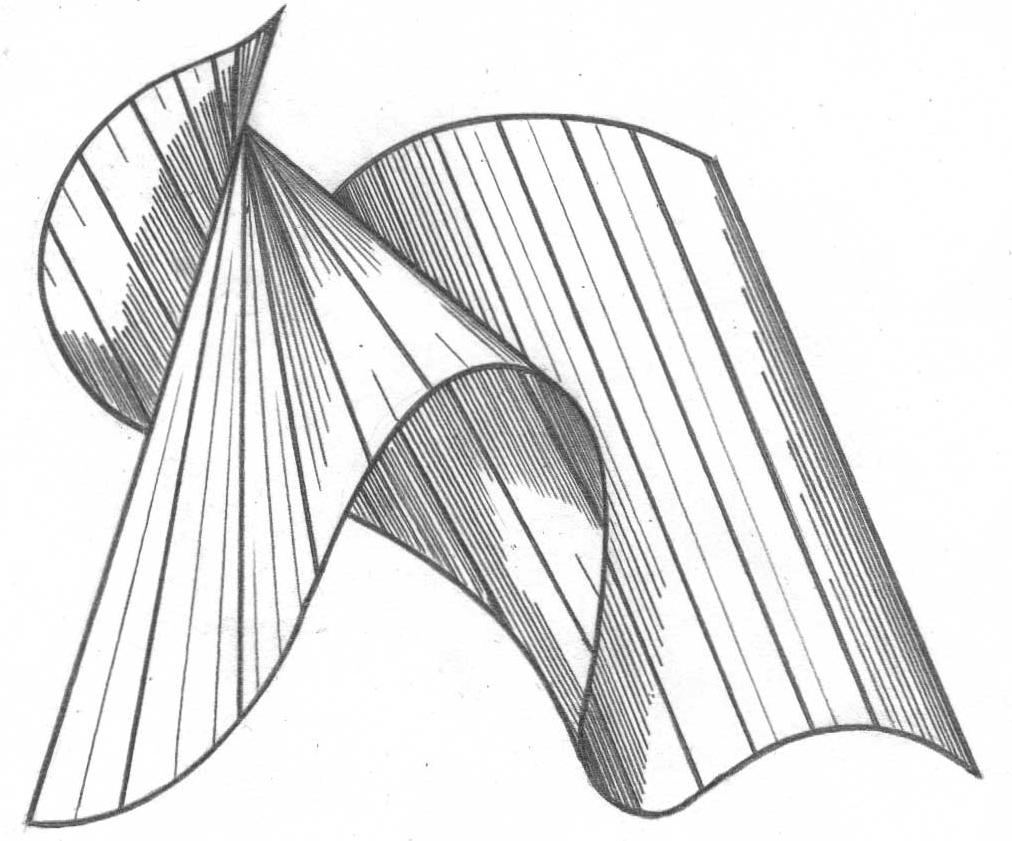

зависимости от формы образующей поверхности подразделяются на линейчатые, у которых образующая есть прямая линия (цилиндр, конус, пирамида, призма и др., рис. 48,50) и нелинейчатые, у которых образующая не является прямой (сфера, тор, рис. 52). Линейчатые поверхности, в свою очередь, подразделяются на развертываемые и неразвертываемые. Развертываемые поверхности, будучи разрезанными по одной из образующих могут быть развернуты в плоскость, т.е. совмещены с плоскостью всеми своими точками без складок, разрывов и выпучивания поверхности или ее частей (цилиндр, конус, призма и др.). Неразвертываемые поверхности при этих же условиях не могут быть совмещены с плоскостью (гиперболический параболоид,

геликоид, цилиндроид), хоть и являются линейчатыми (рис. 54). Нелинейчатые поверхности (сфера, тор и др.) являются неразвертываемыми.

В зависимости от закона формирования (характера перемещения образующей) поверхности подразделяются на:

• винтовые (резьбы, шнеки, червяки, сверла и т.д. - формируются вращательно-поступательным перемещением образующей вокруг и вдоль оси (рис. 55);

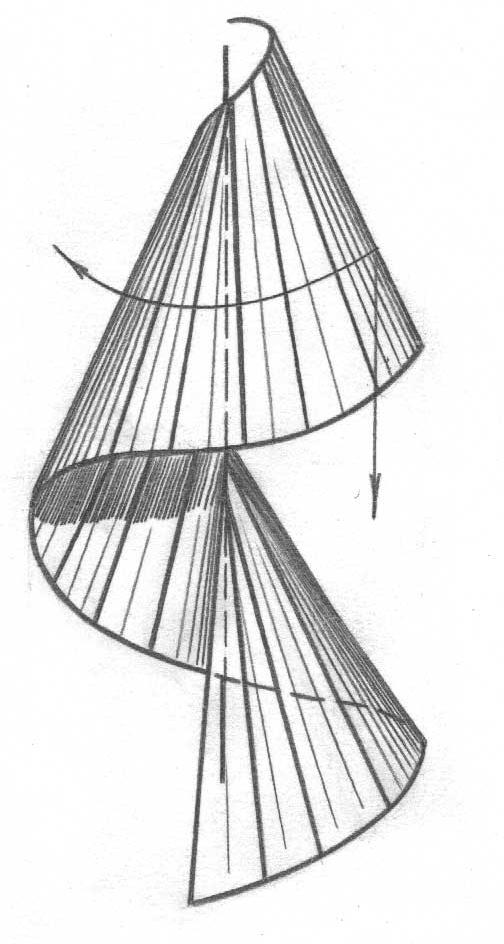
• вращения, - формируются вращением прямолинейной или криволинейной образующей (дуги, окружности, кривой общего вида) вокруг оси. Так образуются цилиндрические, конические, сферические, торовые и т.д. поверхности (рис. 48, 49, 52);

• п

  Рис. 55

  оверхности с плоскостью параллелизма (Каталана), - формируются перемещением прямолинейной образующей l по двум прямолинейным или криволинейным направляющим m

и n (рис. 56) таким образом, что в каждом положении l₁, l₂ … l_i образующая остается параллельной наперед заданной плоскости  (параллелизма).

Для отраслей промышленности, имеющих дело с высокими и сверхвысокими скоростями, при которых среда (газовая, жидкостная и др.) рассматривается как твердое тело (турбиностроение, авиация, космонавтика, военные отрасли) раздел «Поверхности» инженерной графики является основополагающим, поскольку через геометрию поверхностей определяются эксплуатационные, экономические и иные (более высокого порядка) свойства изделий. Естественно, что при таком подходе к тематике требуется совершенно иное количественное и качественное ее рассмотрение.

Рис. 56

5.3 Точка на поверхности

Раздел «Точка на поверхности» в рассматриваемой тематике является весьма ответственным, поскольку его усвоение открывает путь к построению проекций линий на поверхности (как совокупности точек), к определению фигур сечения поверхностей плоскостями общего и частного положения, к построению вырезов на поверхностях и телах (как совокупности линий), к построению линий пересечения поверхностей между собой. Даже простое перечисление круга решаемых задач наталкивает на весьма очевидный вывод: не усвоив этого раздела, дальше в начертательной геометрии делать нечего. До тех пор, пока вы лично не убедитесь в этом, (а это случится непременно) советуем этот довод принять на веру и отнестись к нижеизложенным материалам с повышенным вниманием и ответственностью.

5.3.1 Гранные поверхности

На рис. 57 представлен трехпроекционный чертеж трехгранной пирамиды. Отметим несколько характерных моментов.

Рис. 57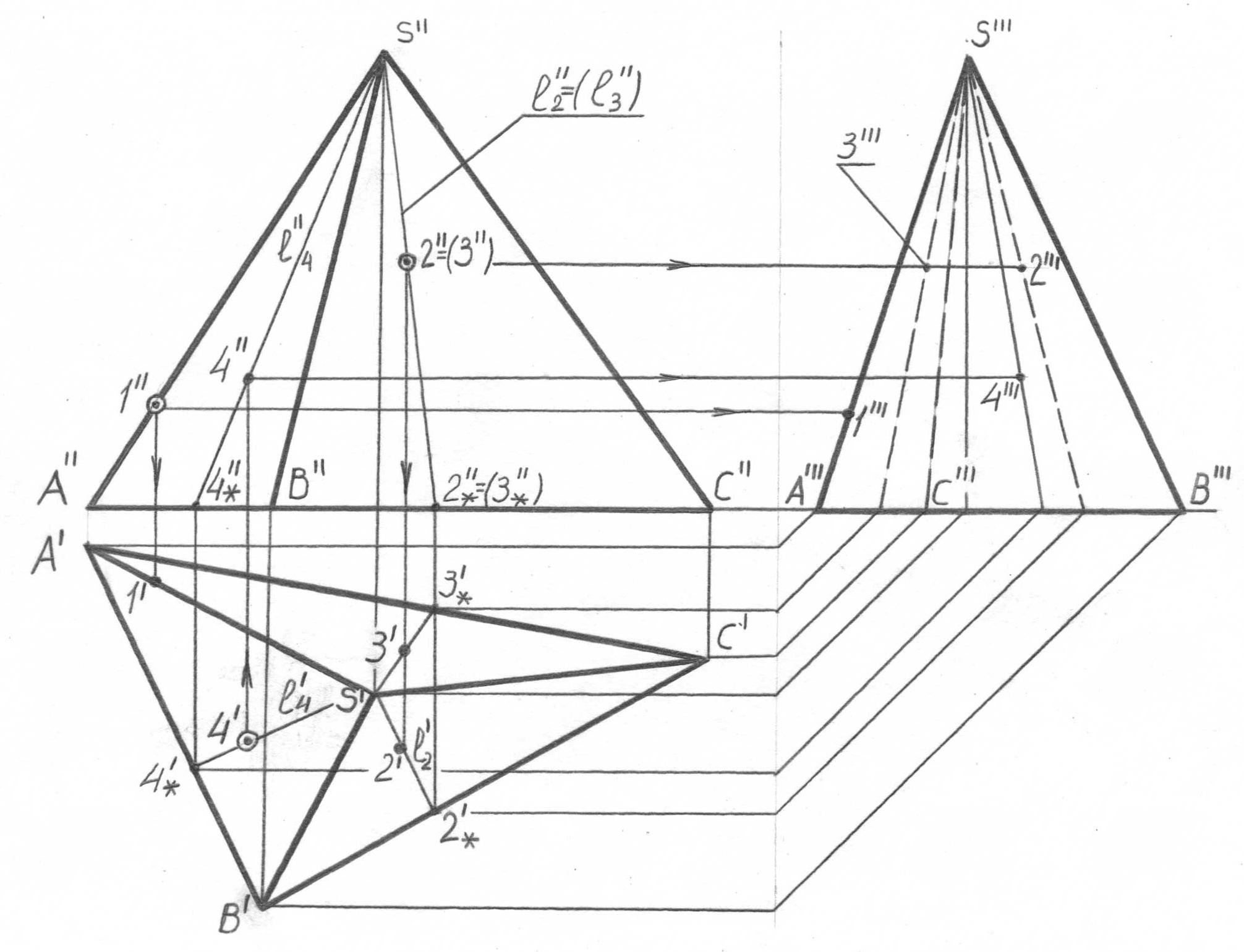

Во-первых, студент должен понять, что на фронтальной проекции все ребра AS, BS, CS – видимые, но грань ASC невидимая, причем ребра AS и CS

являются границами видимости для фронтальной проекции. Для профильной проекции ребра AS и BS являются границами видимости, ребро SC – невидимое. Невидимые грани ASC и BSC закрыты гранью ASB.

Эти положения определяют видимость точек, расположенных на любой грани поверхности.

Во-вторых, если проекция точки задана на любом каком-либо ребре, ее недостающие проекции следует искать только на соответствующих проекциях этого ребра (вспомните свойство параллельного проецирования: если точка принадлежит прямой, проекции точки принадлежат соответствующим проекциям этой прямой). Заданная на фронтальной проекции точка 1 (проекция 1’’) принадлежит ребру AS (проекция A’’S’’), что однозначно определяет положение ее горизонтальной и профильной проекций 1’ и 1’’’ на проекциях A’S’ и A’’’S’’’ этого ребра.

В-третьих, любая грань пирамиды представляет собой плоскость. Тогда задача на принадлежность точки к пирамидальной поверхности сводится к известному условию принадлежности точки к плоскости: точка принадлежит плоскости, если находится на какой-либо прямой этой плоскости. Применительно к поверхности пирамиды в качестве такой «какой-либо» прямой целесообразно принимать образующую, и решение задачи в этом случае сводится к общему алгоритму, показанному на рис. 53.

В-четвертых, каждой видимой точке на фронтальной и профильной проекциях пирамиды соответствует парная невидимая точка, находящаяся в створе видимой (на одной линии визирования). Так, видимая на фронтальной проекции точка 2 (проекция 2’’) и невидимая точка 3 (проекция 3’’ в скобках) находятся на одной линии визирования 2-3 (горизонтальная проекция 2’ – 3’), но каждая из них лежит на своей образующей l₂ и l₃, на фронтальной проекции так же находящихся в створе друг друга: образующая l₂ видимой грани BSC закрывает образующую l₃ невидимой грани ASC (l₂’’ = (l₃’’)).

Исходя из этих характерных моментов аналогичным образом (см. рис. 53) могут быть построены недостающие проекции, например, точки 4, (рис. 57) заданной на горизонтальной проекции или любой другой точки, заданной на любой проекции пирамиды.

На рис. 58 показана трехгранная призма. Здесь тоже следует отметить узловые моменты. Во-первых, каждая грань призмы представляет собой

горизонтально-проецирующую плоскость, а их горизонтальные проекции, - следы-проекции этих плоскостей. Следовательно, горизонтальная проекция любой точки, где бы она ни находилась, может быть расположена только на горизонтальном очерке этой призмы (вспомните: любая точка, линия или плоская фигура, расположенная в проецирующей плоскости, отображается на ее следе-проекции).

Рис. 58

Во-вторых, все точки, расположенные на ее верхнем срезе, на горизонтальной проекции будут видимыми, на любом другом месте каждой грани призмы, - невидимыми.

В-третьих, вопросы видимости граней и точек на них: грани ab и bc на фронтальной проекции – видимые, грань ac – невидимая; грань ab на профильной проекции – видимая, грани ac и cb – невидимые.

С учетом этого точка 1, заданная на верхнем конце фронтальной проекции ребра b (1’’ расположена на b’’), на других проекциях призмы будет видимой (1’, 1’’’) и, естественно, принадлежать соответствующим проекциям b’, b’’’ ребра b. Точка 2, заданная в средней части фронтальной проекции ребра c (см. 2’’), на остальных проекциях (2’, 2’’’) будет невидимой. Точки 3 и 4, заданные на верхних срезах граней bc и ac (см. 3’’ и 4’’), на горизонтальной проекции будут видимыми (см. 3’ и 4’), а на профильной – невидимыми (см. (3’’’) и (4’’’)), т.к. лежат на невидимых гранях. Аналогично горизонтальные проекции точек 7 и 8 будут невидимыми, как и профильная проекция точки 8, находящаяся на невидимой на W грани ac. Если точка 9 на горизонтальной проекции задана как видимая, то ее фронтальная и профильная проекции будут однозначно видимыми. Если горизонтальная проекция точки задана как невидимая (см. 10’), то без дополнительной информации (например, z = 52) ее вертикальные проекции однозначно построить невозможно, что отнюдь не означает неполное задание поверхности.

В заключение отметим еще одну деталь. У студентов традиционно вызывает некоторые осложнения построение профильной проекции поверхности, особенно несимметричной. Это свидетельствует о неважном усвоении темы «проецирование точки», необходимости повторить этот материал и строить каждую проекцию опорных линий поверхности и точек на ней по координатам XYZ (рис. 57). В инженерной практике, как правило, поступают проще: оси y и z не указывают, а значения Y точек откладывают от произвольной точки, принятой по условиям компоновки чертежа за начало координат (рис. 58, фигурная скобка). Кстати, рассмотренные выше соображения по определению недостающих проекций точек на поверхности пирамиды и призмы абсолютно приемлемы для конических и цилиндрических поверхностей соответственно.

5.3.2 Поверхность вращения общего вида

Для облегчения понимания последующего материала предварительно рассмотрим вращение точки А вокруг горизонтально-проецирующей оси i (рис. 59). Здесь важно отметить, что точка А, последовательно перемещаясь из крайнего левого положения А₁ в крайне правое А_i, находится на одном и том же расстоянии от оси i, равном радиусу вращения R. Другими словами, траектория перемещения точки в пространстве есть окружность m радиуса R.

П

Рис. 59

оскольку она находится в горизонтальной плоскости , то на горизонтальную плоскость проекций Н отобразится окружностью m’ действительной величины, а на фронтальную, - в виде отрезка m’’=A₁’’A_n’’ прямой, равного по длине диаметру окружности и параллельного оси х. Это утверждение справедливо для совокупности любым образом расположенных точек (окружности m_1, m₂ … m_i­будут параллельны друг другу и имеют обобщенное название «параллели»).

А теперь представим, что геометрическим местом точек, вращающихся вокруг оси i, является произвольная плоская кривая образующая l, в начальном положении параллельная фронтальной плоскости проекций V (рис. 60). Ее горизонтальная проекция l’ есть прямая, параллельная оси х. При

Рис. 60

вращении образующей l вокруг оси ее точки 1…7 перемещаются по параллелям m₁ … m₇, представляющим собой совокупность однотипных линий дискретного каркаса поверхности. Вторую совокупность линий дискретного каркаса составляют образующие l₁ … l­_I, проекции которых необходимо построить. Горизонтальные проекции образующей l в любом положении останутся радиальными прямыми, т.е. прямыми, продолжение которых проходит через проекцию i’ оси вращения i.

Фронтальная проекция образующей в крайнем правом положении l_n’’ будет зеркальным отображением крайней левой образующей (l’’). Любое промежуточное положение l₁ … l_n-1 образующей l строится через горизонтальную проекцию l₁’ … l_n-1’ по принадлежности каждой из точек 1…7 своей траектории (своей параллели) m₁…m₇ (на фронтальной проекции m₁’’…m₇’’). Другими словами, для построения проекций любого промежуточного положения l₁ образующей l необходимо:

• провести горизонтальную проекцию l₁’ образующей l (это будет радиальная прямая);

• найти точки 1₁’…7₁’ ее пересечения с горизонтальными проекциями параллелей m₁’ …m₇’;

• по линиям проекционной связи снести проекции точек 1₁’…7₁’ на соответствующие фронтальные проекции m₁’’ … m₇’’параллелей m₁…m₇ (точку 1’ сносим на m₁’’ – получаем точку 1₁’’ и т.д. по всем точкам).

Проводим через полученные точки 1’’…7’’ фронтальную проекцию l₁’’ образующей l₁. Чтобы не затемнять чертеж на нем показано только одно промежуточное положение образующей l, хоть аналогичным путем их можно было провести сколько угодно. Таким образом, дискретный каркас поверхности вращения общего вида можно считать построенным.

Рассмотрим характерные опорные линии дискретного каркаса этой поверхности (рис. 60). Параллель наименьшего диаметра называется «горло» или «горловина» (m₂). Параллель наибольшего диаметра называется экватором (m₆). Экватор является границей зоны видимости для горизонтальной проекции поверхности: все, что расположено выше экватора (и не закрыто верхним «отворотом» поверхности) на горизонтальной проекции является видимым; точки и линии, расположенные под экватором, на горизонтальной проекции невидимые.

Л инии пересечения поверхности вращения плоскостью, проходящей через ось вращения i, называется меридианом. Поверхность вращения имеет множество меридианов. Меридиан, параллельный фронтальной плоскости проекций, называется главным фронтальным меридианом. Его фронтальная проекция – есть ничто иное как фронтальный очерк поверхности. Главный фронтальный меридиан является границей зоны видимости для фронтальной проекции: все, расположенное на поверхности проекции до главного фронтального меридиана, на фронтальной проекции является видимым (см. точку А, рис. 60, 61), расположенное за ним, - невидимым (точка В, рис. 61). Ну и, наконец, главный профильный меридиан является границей зоны видимости

Рис. 61

для профильной плоскости проекций (рис. 60). Его фронтальная и горизонтальная проекции есть вертикальные прямые, проходящие через вертикальные оси проекций поверхности, а профильная проекция совпадает с профильным очерком поверхности.

5.3.3 Поверхности вращения второго порядка

Поверхности вращения второго порядка можно рассматривать как частные случаи поверхности вращения общего вида со всеми присущими им положениями и свойствами.

5.3.3.1 Сферическая поверхность

Образуется вращениями окружности или ее части относительно оси, проходящей через центр окружности (дуги). Рассмотрим опорные линии дискретного каркаса этой поверхности. На рис. 62а показаны экватор сферы и его проекции. Горизонтальная проекция экватора совпадают с горизонтальным очерком поверхности (Экв’=Ф’). Фронтальная и профильная проекции экватора представляют собой прямые, параллельные осям x и y соответственно. Верхняя полусфера (со всеми расположенными на ней точками) на горизонтальной проекции, - видимая, нижняя, - невидимая.

На рис. 62б дополнительно к экватору показан главный фронтальный меридиан ФМ и его проекции. Внимательно изучите его расположение на проекциях, сравните с проекциями экватора. Отметьте для себя, что фронтальная проекция ФМ’’ фронтального меридиана ФМ совпадает с фронтальным очерком сферы (ФМ’’ = Ф’’), а горизонтальная и профильная его проекции есть прямые, параллельные осям x и z соответственно. Ближняя полусфера на фронтальной проекции – видимая, дальняя – невидимая.

На рис. 62в показан главный профильный меридиан ПМ и его проекции (для упрощения восприятия экватор и главный профильный

Рис. 62а

Рис. 62б

Рис. 62в

Рис. 62г

меридиан не показаны). Профильная проекция ПМ’’’ профильного меридиана ПМ совпадает с профильным очерком Ф’’’ поверхности, а его горизонтальная и фронтальная проекции и есть прямые, параллельные осям y и z соответственно. Левая полусфера сферы профильной проекции – видимая, правая – невидимая.

А теперь мысленно скомпонуйте рис. 62а, 62б, 62в в одно изображение, представленное на рис. 62г. недостающие проекции точек, заданных на каждой из опорных линий каркаса сферической поверхности, следует отыскивать на соответствующих проекциях именно этих опорных линий с учетом их видимости. Рассмотрите проекции точек 1 и 2 экватора на рис. 62а и 62г, убедитесь в их адекватности. Разберитесь с точками 3, 4 заданными на горизонтальной проекции главного фронтального меридиана (рис. 62г), и с точками 5, 6, заданными на профильной проекции главного профильного меридиана. На своем экземпляре методического пособия можете нанести (карандашом) точки 3, 4, 5, 6 и их проекции на рис. 62б, в. Проекции точек сферы, не принадлежащих опорным линиям ее каркаса, определяются аналогично поверхности вращения общего вида через проекции параллелей (рис. 60, 61 и текст к ним).

5.3.3.2 Коническая поверхность

Как отмечалось выше, в общем случае коническая поверхность формируется перемещением образующей по криволинейной направляющей таким образом, что в каждом положении образующая проходит через общую точку S и пересекает направляющую в какой-то точке (рис. 49б, 50). Если направляющей является окружность, а точка S расположена на перпендикуляре к ее центру, то полученная поверхность носит название «прямой круговой конус» или просто «конус» в общепринятом понимании (рис. 48б).

Как и для любой поверхности вращения, опорными линиями каркаса прямого кругового конуса являются главный фронтальный меридиан (см. ФМ’, ФМ’’ рис. 63а) и главный профильный меридиан (ПМ’, ПМ’’). Условным экватором конуса является его основание. Это означает, что горизонтальные проекции любых точек на поверхности вертикального конуса являются видимыми. Недостающие проекции точек 1…5, заданных фронтальными проекциями, определяются аналогично сфере по принадлежности каждой из них своей опорной линии. Недостающие проекции точек, не принадлежащих опорным линия, могут быть определены как через проекции образующих (см. точки 1, 2 рис. 63б), так и через проекции параллелей (точка 3). Студентам

рекомендуется определить горизонтальные проекции точек 1, 2 через проекции параллелей, а фронтальную проекцию точки 3 через проекцию образующей и убедиться, что результаты будут совпадать абсолютно.

Рис. 63а

Рис. 63б

3.3.3 Цилиндрическая поверхность

Вопрос формирования поверхности прямого кругового цилиндра рассмотрен ранее. Опорные линии каркаса поверхности представлены на рис. 64 (см. ФМ’, ФМ’’, ПМ’, ПМ’’). Отметим, что экватора эта поверхность не имеет. Некоторые характерные моменты, связанные с этой поверхностью, сводятся к следующим.

Во-первых, на горизонтальной проекции все точки, кроме расположенных на верхнем срезе (4, 5, 8) будут невидимыми.

Во-вторых, поскольку любая образующая такого цилиндра является горизонтально-проецирующей линией (как, кстати, и у прямой призмы) горизонтальные проекции любых точек поверхности будут отображаться только на ее горизонтальный очерк Ф’) и сойти с него не могут.

В-третьих, горизонтальная проекция точки 8 (видимая), однозначно говорит о том, что точка расположена на верхнем срезе поверхности.

В

Рис. 64

-четвертых, горизонтальная проекция точки 9 (невидимая) говорит о том, что точка 9 находится где-то ниже верхнего среза поверхности, и для построения ее фронтальной проекции дополнительно необходимо задать аппликату точки (например, 9_z=10). В порядке самоконтроля студентам рекомендуется самостоятельно построить профильные проекции поверхностей и точек, представленных на рис. 63 и 64.

5.4 Сечение поверхности плоскостью частного положения

5.4.1 Общие замечания

Предлагаемая тема является элементом теоретической подготовки студентов к выполнению графического модуля «Проекционное черчение» учебного курса. Рассмотрим ее на примерах решения нескольких однотипных задач применительно к различным поверхностям. Обобщенная формулировка задачи выглядит следующим образом: «построить проекции и действительную величину фигуры сечения поверхности плоскостью частного положения». Обобщающая формализованная запись условия задачи выглядит так:

Предварительно заметим, что линия l пересечения поверхности плоскостью строится по отдельным точкам, общим для плоскости и поверхности. Построение следует начинать с так называемых характерных точек: верхней, нижней, ближней, дальней, левой, правой, границ зон видимости. Если характерных точек окажется недостаточно для выявления формы искомой кривой, находят несколько пар обыкновенных (рядовых) точек. Решают вопрос о видимости точек и последовательности их соединения. Следует отметить, что не в любой задаче каждую из характерных точек можно определить прямым построением. В этом случае в предполагаемой области характерной точки можно задать несколько посредников и через них уточнить ее положение.

5.4.2 Сечение сферы плоскостью частного положения

Для облегчения понимания материала процесс построения линии l разбит на несколько графических фрагментов (рис. 65а-г). В порядке «входа в тему» попытаемся ответить на вопрос о форме искомой линии l в пространстве

Рис. 65а

Рис. 65б

Рис. 65в

Рис. 65г

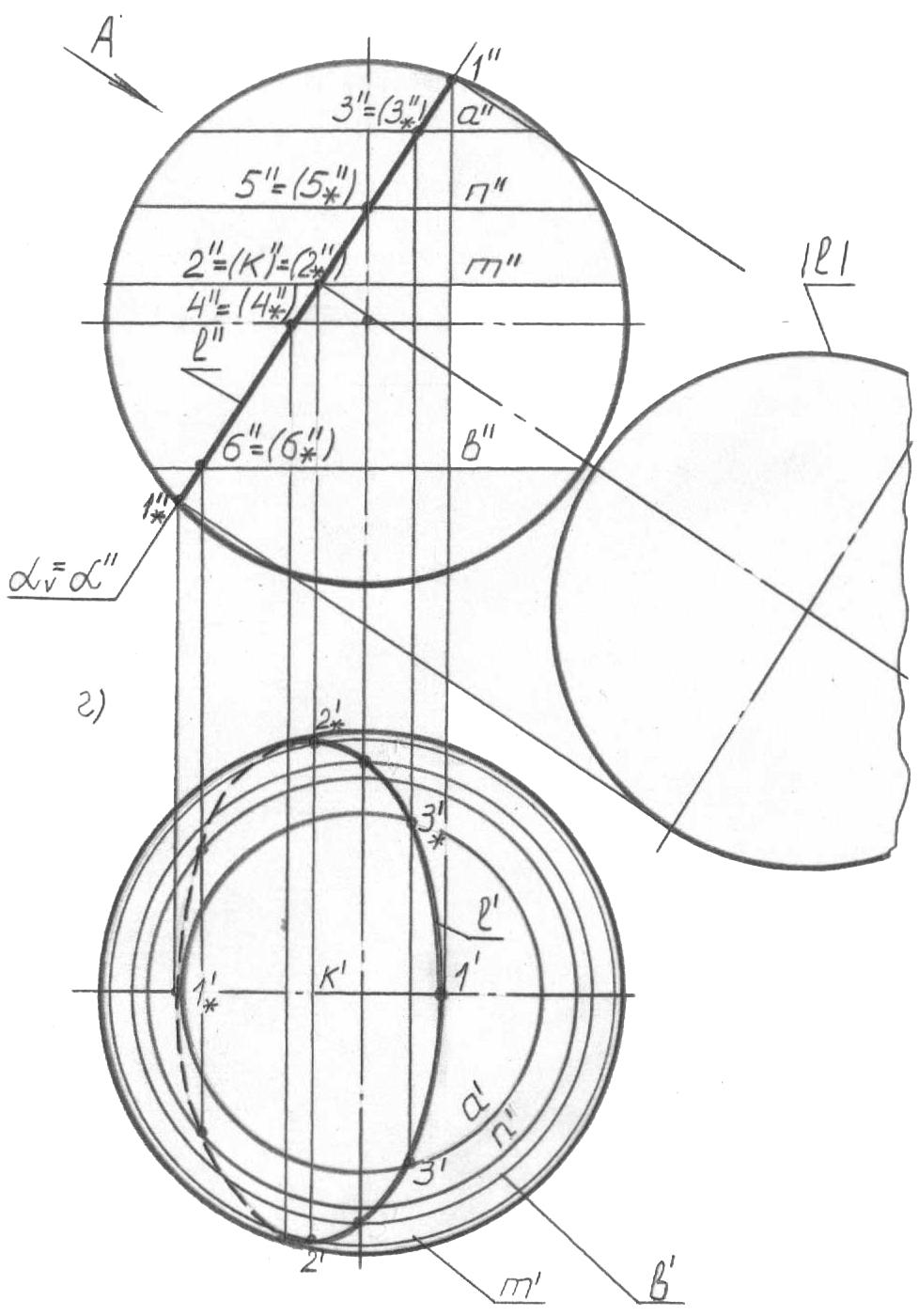
и на проекциях. При этом полезно вспомнить, что в сечении сферы любой некасательной плоскостью всегда будет окружность. В нашей задаче (рис. 65а) плоскость  перпендикулярна фронтальной плоскости. Отсюда следует, что фронтальной проекцией l’’ окружности l будет прямая внутри очерка сферы, совпадающая со следом – проекцией плоскости  (вспомните: «любая точка, линия или плоская фигура, расположенная в проецирующей плоскости, отображается на ее след-проекцию», а линия l принадлежит как поверхности, так и плоскости ). Горизонтальная проекция линии l представляет собой эллипс, поскольку плоскость  не параллельная горизонтальной плоскости проекции. Таким образом, задача сводится к, построению на горизонтальной плоскости H проекции эллипса l, по однозначно определянной фронтальной проекции l’’ = _V = ’’ окружности l.

Из рис. 65б видно, что точка 1 является верхней правой точкой линии l, точка 1_* - нижней левой. Поскольку их проекции 1’’ и 1_*’’ лежат на фронтальной проекции главного фронтального меридиана Ф’’ (см. рис. 62б, г), горизонтальные проекции 1’ и 1_*’ точек должны располагаться на горизонтальной проекции фронтального меридиана (рис. 65б). Так как точка 1_* расположена под экватором, на горизонтальной проекции она будет невидимой (1_*’). Отрезок 1’-(1_­*’) есть малая ось искомого эллипса. Поскольку эллипс является фигурой симметричной, его оси взаимноперпендикулярны и делят друг друга пополам. Отсюда, разделив отрезки 1'-(1_*') и 1'’-(1_*'’) пополам (рис. 65б), получаем проекции k’ и k’’ точки k пересечения осей и заодно – направление большей оси на горизонтальной (перпендикулярно 1'-(1_*')) и фронтальной (2’’ = (k’’) = (2_*’’)) проекциях. Концы 2 и 2_* большей оси эллипса на горизонтальной проекции определяем с помощью параллели m, фронтальную проекцию m’’ которой предварительно проводим через точку 2’’ = (k’’) = (2_*’’). Отметим при этом, что точка 2 является самой ближней, точка 2_* - самой дальней.

Если точка 1 (рис. 65б) видимая, а точка 1_* - невидимая на горизонтальной проекции, то, естественно, на кривой l необходимо определить точку, в которой видимость меняется на обратную. Такой границей для сферы является ее экватор и принадлежащие ему точки 4, 4_* (проекции 4’’ (4_*’’)) кривой l (рис. 65в), горизонтальные проекции которых лежат на горизонтальном очерке сферы. Для двухплоскостного чертежа характерные точки определены, и остается определить несколько пар обычных точек. Их положение на горизонтальной проекции определяется через параллели a, n, b, предварительно произвольно заданные на фронтальной проекции. А теперь отдельные фрагменты (рис. 65а-в) объединим на одном изображении, добавив сюда обыкновенные точки 3, 3_* (рис. 65в), 5, 5_* и 6, 6_* (рис. 65г). Это и есть результат решения поставленной задачи.

Действительная величина |l| фигуры сечения сферы плоскостью  в общем случае определяется известными способами преобразования комплексного чертежа, например, способом замены плоскостей проекций. Применительно к рассматриваемой задаче, когда форма кривой наипростейшая и симметричная, действительная величина фигуры сечения может быть определена простой логикой: если смотреть на сечение в направлении, перпендикулярном плоскости  (стрелка А, рис. 65г), увидим фигуру сечения в действительную величину в виде окружности диаметром, равным отрезку 1’’-2’’. Проводим ее по линиям связи, перпендикулярным .

5.4.3 Коники

Поверхность прямого кругового конуса занимает особое положение среди других поверхностей. Она уникальна тем, что является носителем совокупности кривых второго порядка: окружности 2 (рис. 66а), эллипса 3 (рис. 66а), параболы 5 (рис. 66б) и гиперболы 6 (рис. 66в), которые получаются при сечении конуса различно расположенными плоскостями. Окружность получается когда секущая плоскость ₂ перпендикулярна оси конуса; эллипс – когда плоскость ₃ не перпендикулярна оси и пересекает обе очерковые образующие конуса; парабола – когда плоскость ₅ параллельна очерковой

Рис. 66а

Рис. 66б

Рис. 66в

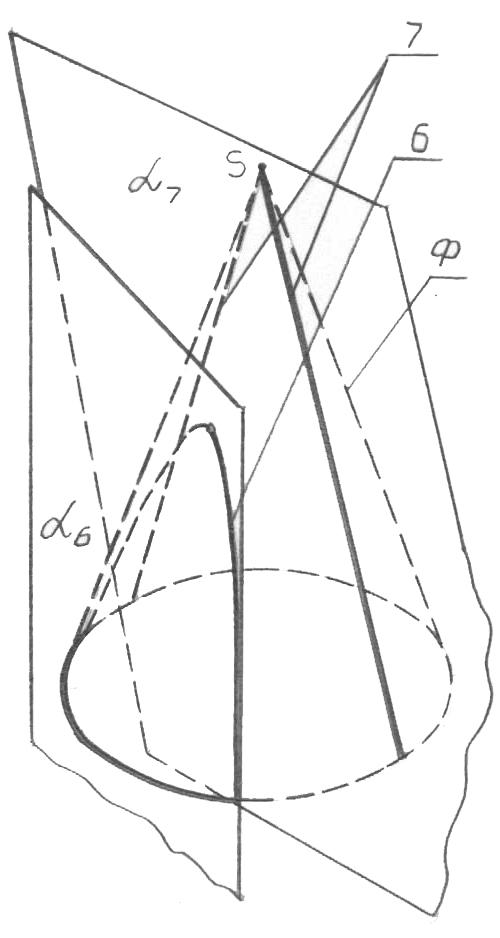
образующей, а гипербола – когда плоскость ₆ занимает положение между плоскостью ₅ и параллельной оси конуса. Помимо этого, сечение конуса плоскостью, проходящей только через вершину S, дает точку 1 (рис. 66а),

плоскостью ₄, касательной к конусу, - прямую (рис. 66б), а плоскостью ₇, проходящей через вершину S и основание конуса, - две прямые (рис. 66в).

Для самопроверки студентам рекомендуется построить горизонтальные и фронтальные проекции линий 2 – 7, руководствуясь положениями п. 5.3.3.2 и рис. 63.

5.4.4 Сечение конуса плоскостью частного положения

Условие задачи, его формализованная запись и ход рассуждений при ее решении аналогичны вышеописанным. Сразу определимся, что за линии будут в сечении и на проекциях. По расположению секущей плоскости  (рис. 67а) однозначно отвечаем: в пространстве и на горизонтальной проекции, - парабола, на фронтальной проекции – прямая, совпадающая со следом проекцией _V = ’’ секущей плоскости ; то есть задача сводится к построению горизонтальной проекции l’параболы l и ее действительной величины |l|.

О

Рис. 67а

пределяем характерные точки. Точка 1 – верхняя, правая; точки 2 и 2_* - нижняя ближняя и нижняя дальняя

соответственно. Точка 1 находится на главном фронтальном меридиане, точки 2, 2_* - на условном экваторе (на основании) конуса, что и определяет их горизонтальные проекции по принадлежности. Других характерных точек нет. Остается взять несколько пар обычных точек под номерами 3, 4, 5 (рис. 67б). Их положение на фронтальной проекции задается совершенно произвольно

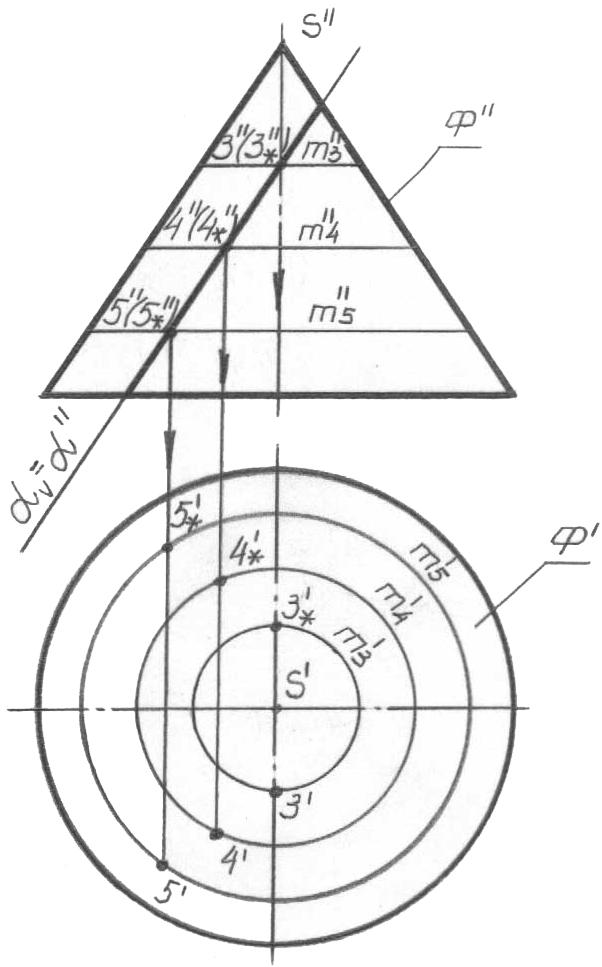(желательно более-менее равномерно), а горизонтальные проекции определяются через соответствующие параллели m₃, m₄, m₅ (см. также раздел 5.3.3.2 и рис. 63). Сведите изображения (рис. 67а, б) в обобщающее изображение (рис. 67в), являющееся результатом решения задачи.

В

Рис. 67б

основу построения действительной величины фигуры сечения l положен метод замены плоскостей проекций. При этом рассуждаем следующим образом. Поскольку на горизонтальной проекции линия l спроецировалась

с искажением, логично эту

традиционно горизонтальную плоскость проекций заменить на другую тоже горизонтальную, но не параллельную H, а параллельную  плоскость. Тогда ось x_1,1 новой системы плоскостей (см. раздел 4 «Способ замены плоскостей проекций») V/H₁, будет параллельна _V’’. Положение этой оси x_1,1 можно задать на любом свободном поле чертежа. Поскольку парабола является симметричной кривой для удобства построений начальную системы осей xyz задаем через центр S’. Тогда построение точек действительной величины линии l сведется к откладыванию отрезков равных величин (см. размеры в фигурных скобках), взятых с прежней горизонтальной проекции, на соответствующую линии проекционной связи новой системы x_1,1 V/H₁. Эти отрезки есть ничто, иное как значения Y каждой точки, в старой системе плоскостей проекций.

Рис. 67в

Например, отрезок S’3_*’ следует отложить в новую систему с осью x_1,1 вправо и влево от оси x_1,1, отрезок 4_*’x – по своей линии связи и т.д. до последней пары точек под номером 2.

Действительную величину фигуры сечения в общем случае можно строить в проекционной связи, как только что описано, со смещением (см. изображением с осью x_1,2) и со смещением и поворотом (см. изображение с осью x_1,3). В последних двух случаях из-за нарушения проекционных связей следует обеспечить вдоль осей x_1,2 и x_1,3 равенство расстояний между линиями связи отрезкам 1’’-3’’(3’’) – 4’’(4_*’’) и т.д. до точек 2’’(2_*’’). При этом за начало построений может быть принята любая точка 1₀, расположенная где угодно на новой оси. Принятый Вами из трех вариантов построения действительной величины фигуры сечения определяется условиями компоновки изображений на чертеже в каждом конкретном случае. В заключение отметим, что традиционное (кстати, более привычное для студентов) расположение координатных осей между горизонтальной и фронтальной проекциями конуса привело бы к смещению вправо изображения искомой линии |l| относительно осей x_1,1, x_1,2, x_1,3 без нарушения ее формы и сделало бы менее удобным само построение линии |l|.

5.4.5 Сечение пирамиды плоскостью частного положения

П

Рис. 68

оскольку пирамида (рис. 68) представляет собой гранную поверхность, искомая линия l в пространстве и на горизонтальной проекции будет многоугольником (в нашем случае – треугольником). Как и в предыдущих случаях (см. рис. 65, 68), фронтальная проекция l’’ линии l совпадает со следом-проекцией секущей плоскости . Задача сводится к определению точек 1, 2, 3 (рис. 68) пересечения каждого из ребер пирамиды с плоскостью . Так как плоскость  перпендикулярна фронтальной плоскости проекций искомые точки

1, 2, 3 являющиеся общими и для

ребер и для плоскости , будут представлять собой точки 1’’, 2’’, 3’’ пересечения проекции каждого ребра со следом проекцией _V = ’’ плоскости . Горизонтальные проекции 1’, 2’, 3’ точек определяются по их принадлежности каждому ребру. Так как плоскость  не параллельна основанию АВС пирамиды, ни одна из сторон треугольника 1’2’3’ не должна быть параллельна соответствующим сторонам основания A’B’C’.

Поскольку форма сечения несимметричная, для построения действительной величины фигуры сечения расположение оси x в начальной системе V/H задаем традиционным, т.е. совпадающим с основанием пирамиды. Проводим ось х₁ параллельно плоскости  и линии проекционной связи (перпендикулярные _V = ’’ из точек 1’’, 2’’, 3’’) для определения местоположения на них точек 1₀, 2₀, 3₀. По линии связи точки 3 откладываем на сечении расстояние Y_3, взятое от оси x до горизонтальной проекции 3’ точки 3. аналогично поступаем с точками 2 и 1, получая в итоге точки 3₀, 2₀, 1₀, определяющие истинную форму искомого треугольника.

5.4.6 Сечение призмы плоскостью частного положения

Аналогично рассмотренным на рис. 65, 67, 68 примерам, фронтальная проекция фигуры сечения призмы плоскостью  (рис. 69) совпадает со следом-проекцией плоскости . В пространстве и на горизонтальной проекции линия l будет четырехугольником (по числу граней призмы). Так как каждая грань рассматриваемой призмы представляет собой горизонтально-проецирующую плоскость, а ребра a, b, c, d –

Рис. 69

горизонтально-проецирующие

прямые, горизонтальные проекции 1’, 2’, 3’, 4’ точек пересечения ребер призмы с плоскостью  совпадают с горизонтальными проекциями a’, b’, c’, d’ соответствующих ребер. Другими словами, горизонтальная проекция фигуры сечения совпадает с горизонтальным очерком поверхности. Действительная величина |l| фигуры сечения l построена в проекционной связи аналогично рис. 68.

5.4.7 Сечение цилиндра плоскостью частного положения

Н

Рис. 70

а рис. 70 показаны проекции и действительная величина фигуры сечения прямого кругового цилиндра фронтально-проецирующей плоскостью . Поскольку цилиндр занимает горизонтально-проецирующее положение, горизонтальные проекции всех точек линии l, располагаются на горизонтальном очерке

поверхности, т.е. горизонтальная

проекция линии l представляет собой окружность.

Действительная величина фигуры сечения представляет собой эллипс, построенный со смещением и поворотом. Порядок построения, его аналогичен рис. 67. Текущие значения координаты Y точек 2₀, 3₀ и др. показаны фигурными скобками.

Рассмотренная тематика позволяет осуществить построение проекций и действительной величины фигуры сечения предметов практически любой конфигурации, представляющей собой совокупность нескольких элементарных геометрических форм.

5.5 Пересечение поверхностей

5.5.1 Общий алгоритм построения линии пересечения поверхностей

Для построения линии пересечения поверхностей Ф₁ и Ф₂ (рис. 71) необходимо.

1. П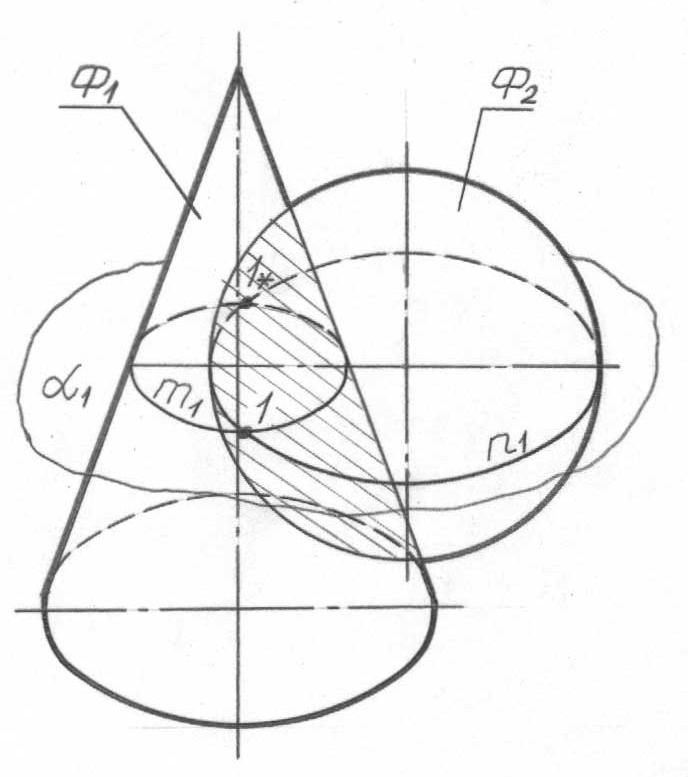ересечь заданные поверхности вспомогательным геометрическим элементом – посредником (α₁).

2. Построить линии (m₁ и n₁) пересечения посредника (α₁) с каждой поверхностью в отдельности.

3. Н

   Рис. 71

   айти точки (1 и 1_*) пересечения полученных

линий (m₁ и n₁).

4. Повторить этот алгоритм необходимое количество раз (на рис. 71 это не показано).

5. Соединить между собой полученные точки (1, 1_*, 2, 2_* и т.д.) в надлежащей последовательности. Символическая запись порядка построения выглядит следующим образом.

1. α₁ ∩ Ф₁ = m₁; α₁ ∩ Ф₂ = n₁; m₁ ∩ n₁ = 1, 1_* – первый шаг.

2. α₂ ∩ Ф₁ = m₂; α₂ ∩ Ф₂ = n₂; m₂ ∩ n₂ = 2, 2_* – второй шаг.

и т.д.

i) α_k∩ Ф₁ = m_k; α_k ∩ Ф₂ = n_k; m_k ∩ n_k = k, k_* – последний шаг.

l = {1, 1_*, 2, 2_*, ... k, k_*}.

Для значительного облегчения и обеспечения четкости решения любой задачи на пересечение поверхностей рекомендуется внутри каждого шага алгоритма присваивать один и тот же индекс всем элементам построения, т.е. посредник, например с индексом 5 дает линии m₅ и n₅, пересечение которых дает точки под номером 5 со своими отличительными признаками (5_*, 5₀, 5., 5_∆ и т.д.).

5.5.2 Общие замечания

1. В общем случае в качестве посредников могут приниматься плоскости общего положения, плоскости частного положения, концентрические или эксцентрические сферы, цилиндры и т.д. в зависимости от конкретной графической задачи.

2. Посредник должен выбираться таким (по виду) и так (по расположению), чтобы линии m и n были наипростейшими (окружности, прямые, совокупности прямых).

3. Точки 1, 2 и т.д. искомой линии l должны располагаться в пределах площади взаимного наложения проекций пересекающихся поверхностей (затемненная зона рис. 71).

4. Построение следует начинать с так называемых "характерных" точек: верхней, нижней, левой, правой, ближней, дальней, границ зон видимости и т.д. Если характерных точек окажется недостаточно для однозначного определения характера искомой линии, необходимо найти несколько так называемых "обыкновенных" точек.

5. Если пересекающиеся поверхности имеют общую плоскость симметрии, параллельную какой-либо плоскости проекций, то пересечение их очерков дает пару характерных точек, а остальные точки (в том числе и характерные) находятся в створе друг друга.

6. Порядок линии пересечения численно равен произведению порядков пересекающихся поверхностей.

7. Вопросы видимости – невидимости точек и последовательности их соединения решаются для каждой задачи в отдельности.

5.5.3 Метод плоских посредников

От наглядного представления сути алгоритма, показанного на рис. 71, перейдем непосредственно к построению линии пересечения этих поверхностей на двухплоскостном чертеже (рис. 72). Формализованная запись условия задачи выглядит следующим образом:

Ф ₁, Ф₂; Ф₁ ∩ Ф₂ = l?

Рис. 72а

Анализ и решение задачи.

1. Пересекаются две поверхности вращения второго порядка, следовательно, искомая линия l будет четвертого порядка.

2. Так как вид пересечения – "врезка" (несквозное пересечение), то линия l будет одна.

3. Поверхности имеют общую плоскость симметрии α₁, параллельную фронтальной плоскости проекций (рис. 72а), значит пересечение их фронтальных очерков Ф₁'' и Ф₂'' дает пару характерных точек: 1'' – верхнюю и 1_*'' – нижнюю. Кстати, заметим, что использование плоскости α₁ в качестве первого посредника дает тот же результат, поскольку линии m₁'' и n₁'' есть ничто иное, как фронтальные очерки поверхностей.

4. В качестве посредников для последующих построений в этой задаче целесообразно принимать горизонтальные плоскости α₂, α₃ и т.д., поскольку линии пересечения ими каждой из поверхностей (см. рис. 72 а,б) являются наипростейшими (окружностями).

5. Границей зоны видимости искомой кривой l для горизонтальной плоскости проекций является экватор сферы, поэтому плоскость – посредник α₂, проведенная через экватор сферы Ф₂, дает на втором шаге алгоритма принадлежащие экватору точки 2 и 2_*, являющиеся границами зоны видимости для горизонтальной плоскости проекций. Эти же точки являются самыми левыми.

6. Границами видимости для фронтальной плоскости проекций являются главные фронтальные меридианы пересекающихся поверхностей и принадлежащие им точки 1 и 1_*. За счет наличия общей плоскости симметрии α₁, параллельной фронтальной плоскости проекций, невидимая часть искомой линии l на плоскости V полностью закроется ее видимой частью кривой (о чем свидетельствует двойное обозначение точек 2(2_*)) и т.д. Других характерных точек в рассматриваемой задаче нет.

Рис. 72б

Таким образом, построение линии пересечения поверхностей сводится к следующему.

Во-первых, (рис. 72а) проводим плоскость α₁, параллельную фронтальной плоскости проекций через оси i и j поверхностей. На горизонтальной плоскости проекций – это след-проекция α_1Н = α₁', параллельная оси х. На фронтальной проекции находим точки 1'' и 1_*'' пересечения очерков Ф₁'' и Ф₂''. Сносим полученные точки на горизонтальный след-проекцию α_1Н = α₁' плоскости α₁ с учетом их видимости (точка 1' – видимая, точка 1_*' – невидимая). Записываем первый шаг алгоритма в виде:

1) α₁ || V; α₁ i, j; α₁ ∩ Ф₁ = m₁; α₁ ∩ Ф₂ = n₁; m₁ ∩ n₁ = 1, 1_*.

Точка 1 – верхняя, точка 1_* - нижняя.

Отметим, что алгоритм записывается для пространства, а построение проекций точек и линии l производится для каждой плоскости проекций с обязательным обозначением каждого элемента построения.

Во-вторых, через экватор сферы Ф₂ проводим плоскость-посредник α₂, параллельную горизонтальной плоскости проекций (см. α_2V = α₂''). Параллели m₂ и n₂ фронтальной проекции неразличимы, так как их проекции m₂'' и n₂'' частично накладываются друг на друга. Поэтому находим их горизонтальные проекции m₂' и n₂', как окружности соответствующих радиусов и точки 2' и 2_*' их пересечения. Фронтальные проекции 2'' и 2_*'' этих точек находим на следе-проекции α_2V = α₂'' плоскости α₂ по линиям проекционной связи. Записываем второй шаг алгоритма.

2) α₂ || Н; α₂ ∩ Ф₁ = m₂; α₂ ∩ Ф₂ = n₂; m₂ ∩ n₂ = 2, 2_*.

Обе точки – границы видимости для плоскости Н.

В-третьих, произвольно проводим плоскость α₃, параллельную плоскости Н. Аналогично второму шагу, находим горизонтальные проекции m₃' и n₃' линий пересечения этой плоскости с каждой поверхностью и горизонтальные проекции 3' и 3_*' точек 3 и 3_*, а затем на следе-проекции α_3V = α₃'' – фронтальные проекции 3'' и 3_*'' этих точек. Записываем третий шаг алгоритма.

3) α₃ || Н; α₃ ∩ Ф₁ = m₃; α₃ ∩ Ф₂ = n₃; m₃ ∩ n₃ = 3, 3_* - обычные точки.

Аналогично можно было получить точки под номером 4:

4) α₄ || Н; α₄ ∩ Ф₁ = m₄; α₄ ∩ Ф₂ = n₄; m₄ ∩ n₄ = 4, 4_* - обычные точки.

и этого для рассматриваемой задачи достаточно.

Определяем порядок соединения точек между собой, предварительно объединив рис. 72а и рис. 72б в одно изображение (рис. 72в). Поскольку искомая кривая l является замкнутой, ее построение можно начинать с любой точки и в любом направлении, например 1, 2, 3, 4, 1_*, 4_*, 3_*, 2_*, 1. Заключительная фраза алгоритма может быть записана в виде:

l = {1, 2, 3, 4, 1_*, 4_*, 3_*, 2_*, 1}

Пример оформления задачи представлен на рис. 72в.

Рис. 72в

5.5.4 Метод концентрических сфер

Применение этого метода основано на теореме о пересечении соосных поверхностей. Соосными называются поверхности, имеющие общую ось вращения. Сущность теоремы сводится к следующему: линией l пересечения двух соосных поверхностей вращения является окружность (параллель), проекция которой l’’ на плоскость, параллельную общей оси вращения есть прямая линия, а на плоскость, перпендикулярную общей оси вращения, - есть окружность l’ действительной величины (рис. 73а). Это принципиальное положение справедливо для любого пространственного положения (сравните рис. 73а и рис. 73б) любых соосных пересекающихся поверхностей. В заключение отметим, что две пересекающиеся любым образом сферы всегда соосны, поскольку проходящая через их центры прямая всегда является их общей осью вращения.

Рис. 73а

Рис. 73б

Рассмотрим задачу построения линии пересечения поверхностей с использованием метода концентрических сфер на примере прямого кругового конуса и кругового цилиндра. Для упрощения понимания на рис. 74 дано поэтапное решение задачи. Предварительно сформулируем условия применения этого метода. Их три. Во-первых, пересекающиеся поверхности должны быть поверхностями вращения. Во-вторых, оси поверхностей должны пересекаться. В-третьих, поверхности должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций. Эти условия должны выполняться одновременно. Отметим, что применение метода концентрических сфер не исключает использования любых других посредников, дающих нужный результат наипростейшим путем.

Некоторые преимущества метода концентрических сфер заключаются в том, что он позволяет получить искомую линию пересечения поверхностей на единой проекции (без привлечения построений на других плоскостях проекций). Однако, и в учебном процессе, и в инженерной практике это преимущество не стоит преувеличивать.

Рис. 74а

Рис. 74б

Рис. 74в

Сферические посредники должны проводиться из точки пересечения осей поверхностей, поскольку только в этом случае они (посредники) окажутся соосными с каждой из пересекающейся поверхностей. В качестве минимального посредника должна приниматься большая из сфер (Р₂, рис. 74а), вписанных из точки пересечения осей (i и j) в каждую поверхность в отдельности. Это связано с тем, что меньшая из вписанных сфер (Р₀) не дает линии пересечения (или касания) с другой поверхностью (Ф₁) и, следовательно, не дает точки, общей для пересекающихся поверхностей. В качестве максимального посредника принимается сфера (Р₁, рис. 74б), радиус которой равен расстоянию от точки пересечения осей i и j до наиболее удаленной точки (1_*, рис. 74а) пересечения очерков поверхностей Ф₁ и Ф₂. Остальные сферические посредники должны быть больше минимального и меньше максимального.

Анализ и решение задачи.

1. Пункты 1-3 из предыдущей задачи (рис. 72) один к одному справедливы для рассматриваемого примера.

2. Для определения минимального посредника Р на фронтальной плоскости проекций (рис. 74а) проводим сферы Р₀ и Р₂ (проекции Р₀'' и Р₂''), вписанные соответственно в поверхности Ф₂ и Ф₁ (проекции Ф₂'' и Ф₁''). В качестве минимального посредника принимаем сферу Р₂ (проекция Р₂''), отвергая Р₀ (проекция Р₀''), как не дающую линию m₀ пересечения с поверхностью конуса Ф₁ (проекция Ф₁''). Через точки касания сферы Р₂ (проекция Р₂'') с конусом Ф₁ (проекция Ф₁'') проводим линию m₂ (проекция m₂'') касания (напомним, что касание – есть частный случай пересечения) ее с конусом Ф₁ (проекция Ф₁''), а через точки пересечения Р­₂ (проекция Р₂'') с цилиндром Ф₂ (проекция Ф₂'') – линию n₂ (проекция n₂'') пересечение посредника Р₂ с цилиндром Ф₂. Находим точки 2'', 2_*'' пересечения линий (в пространстве – окружностей) m₂'' и n₂''. Находим горизонтальную проекцию m₂' параллели m₂ и по линии связи сносим на нее точки 2', 2_*'. Записываем второй шаг алгоритма.

2. Р₂ > P₀ - минимальная сфера. Р₂ ∩ Ф₁ = m₂; Р₂ ∩ Ф₂ = n₂; m₂ ∩ n₂ = 2, 2_* - левые точки. В качестве максимального посредника принимаем сферу Р₁ (рис.74б), проходящую через ранее полученную точку 1_* (проекция 1_*''). Остальные сферические посредники должны быть радиусом больше Р₂ и меньше Р₁.

3. Для определения границы зоны видимости горизонтальной проекции искомой линии l через условный экватор цилиндра Ф₂ (через ось j) проводим горизонтальную плоскость уровня α₃ (след проекция α_3V = α₃''). Эта плоскость α₃ пересекает конус Ф₁ по окружности m₃ (проекция m₃''), а цилиндр Ф₂ по прямоугольнику, фронтальная проекция которого есть прямая n₃'', а горизонтальная проекция n₃' совпадает с горизонтальным очерком Ф₂' цилиндра Ф₂. Горизонтальные проекции m₃' и n₃' линий m₃ и n₃, пересекаясь, дают точки 3 и 3_* (проекции 3' и 3_*'). Фронтальные проекции 3'' и 3_*'' этих точек находятся на следе-проекции α_3V = α₃'' плоскости α₃ по линиям проекционной связи. Записываем третий шаг алгоритма.

3. α₃ || Н; α₃ j; α₃ ∩ Ф₁ = m₃; α₃ ∩ Ф₂ = n₃; m₃ ∩ n₃ = 3, 3_*. – границы видимости для горизонтальной плоскости проекций, одновременно являющиеся ближней и дальней точками.

На этом характерные точки заканчиваются, и следует перейти к построению обыкновенных точек.

4. Проводим сферический посредник Р₄, больший Р₂ и меньший Р₁ (проекция Р₄''). Находим фронтальные проекции m₄'' и n₄'' линий m₄ и n₄ пересечения посредника Р₄ с поверхностями конуса и цилиндра и точки m₄'' и n₄'', пересечения этих линий. Строим горизонтальную проекцию m₄' параллели m₄ и на ней по линии связи – горизонтальные проекции 4', 4_*' искомых точек. Записываем четвертый шаг алгоритма.

4. Р₁ > P₄ > P₂; Р₄ ∩ Ф₁ = m₄; Р₄ ∩ Ф₂ = n₄; m₄ ∩ n₄ = 4, 4_*.

5. Аналогично решается и записывается последний пятый шаг алгоритма.

5. Р₁ > P₅ > P₂; Р₅ ∩ Ф₁ = m₅; Р₅ ∩ Ф₂ = n₅; m₅ ∩ n₅ = 5, 5_*.

и заключительная фраза алгоритма

l  {1,2,3,4,5,1_*,5_*,4_*,3_*,2_*,1}

Объединив рис. 74а и рис. 74б на одном изображении, получите окончательное решение задачи в виде рис. 74в, на котором дан пример оформления этого задания.