Раздел 4. Метод перемены плоскостей проекций

Проецируемая фигура может занимать по отношению к плоскостям проекций удобное (выгодное, рациональное) и неудобное (невыгодное, нерациональное) положение. Задачи решаются значительно проще в случае частного положения геометрической фигуры относительно какой-либо плоскости проекций. При этом наиболее выгодным частным положением проецируемой фигуры следует считать положение, перпендикулярное или параллельное по отношению к какой-либо плоскости проекций.

Применяя способ перемены плоскостей проекций, данную геометрическую фигуру оставляют неподвижной. Новые плоскости проекций устанавливают так, чтобы получаемые на них проекции обеспечивали рациональное решение рассматриваемой задачи, причем каждая новая система плоскостей проекций должна быть системой ортогональной (прямоугольной).

На рис. 38 дана точка А, заданная в системе плоскостей проекций H и V. Такую систему обозначим . Заменим одну из них, например V другой, также вертикальной плоскостью V­₁ и построим новую фронтальную проекцию точки на эту плоскость. Плоскость V₁ пересекается с плоскостью Н по прямой х₁, которая определяет новую ось проекций. Так как горизонтальная плоскость проекций Н является общей для обеих систем, то координата Z точки А остается неизменной. Переход от исходной система плоскостей проекций к новой осуществлен при неизменной координате z.

Следовательно, расстояние от новой фронтальной проекции до новой оси х₁ равно расстоянию от заменяемой проекции до оси х, т.е. А₁’’А_х1 = А’’А_х. При этом точка А₁’’ определена как основание перпендикуляра, опущенного из

Рис. 38а

Рис. 38б

точки А на плоскость V₁. Что же касается горизонтальной проекции А’, то она остается прежней.

Аналогично можно заменить горизонтальную плоскость проекций Н на плоскость Н₁ также перпендикулярную V. Преобразование ортогональных плоскостей проекций выразится следующим образом:

На этот раз не изменится величина координаты Y, которая определяет расстояние точки А до общей для двух систем плоскости проекций V (рис. 39).

Рис. 39а

Рис. 39б

Поэтому А₁’А_х1 = А’А_х. При построении новой проекции точки на эпюре (рис. 39б) из А’’ опущен перпендикуляр на новую ось x₁, на котором от точки А_х1 отложен отрезок А₁’A_x1, равный координате Y точки А. Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило. Расстояние от новой проекции точки до новой оси должно равняться расстоянию от преобразуемой (заменяемой) проекции точки до предыдущей оси. Если объектом рассмотрения является не точка, а любой другой геометрический объект, подобные преобразования производятся для каждой его характерной точки. При этом на каждом этапе положение новой оси задается не произвольно, а так, как это выгодно для решения конкретной графической задачи.

Все задачи, решаемые способом перемены плоскостей проекций, можно свести к одной из следующих четырех задач.

Задача 1. Преобразовать чертеж так, чтобы прямая общего положения оказалась параллельной одной из плоскостей проекций новой системы.

Н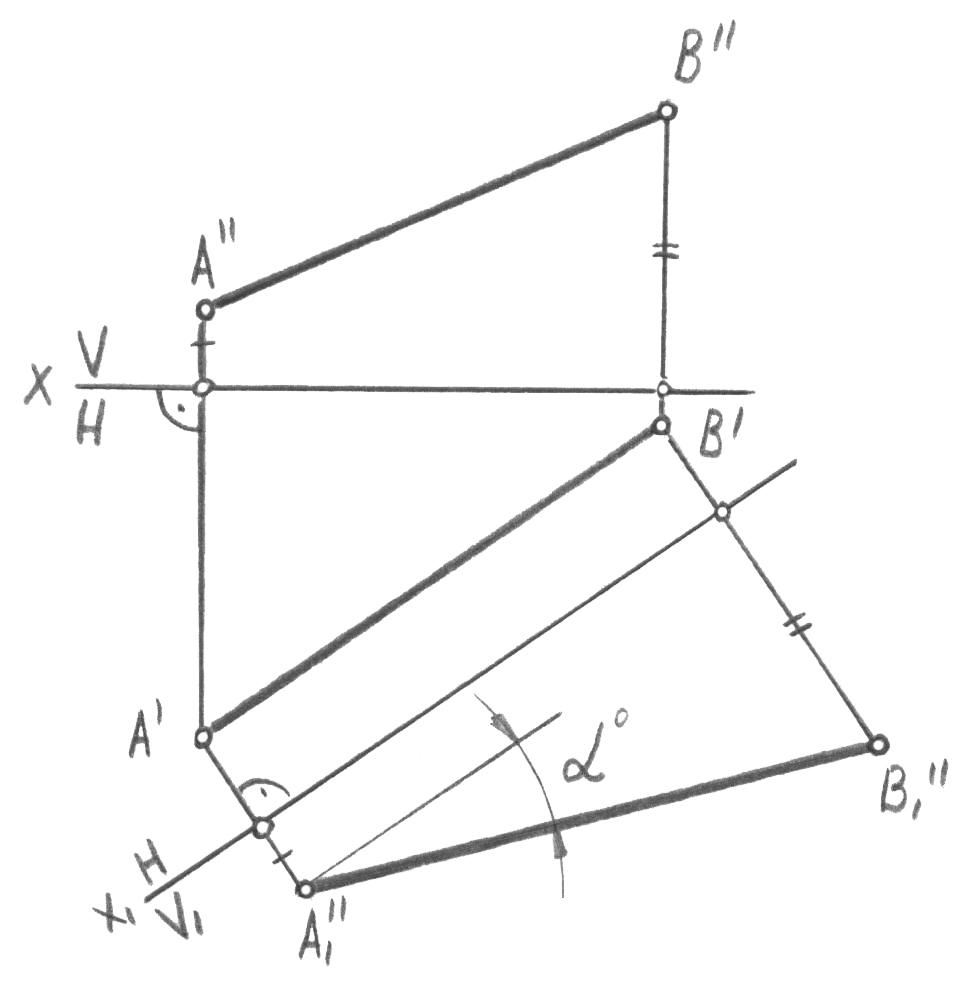а рис. 40 показан отрезок прямой [АВ], который в исходной системе плоскостей проекций занимает общее положение.

Д

Рис. 40

ля решения задачи взята новая плоскость V₁, отвечающая двум условиям: V₁  H и V₁ || [AB]. В системе данный отрезок прямой стал фронталью, и поэтому спроецировался в натуральную величину. Угол между проекцией [A₁’’B₁’’] и осью x₁ является углом ⁰ наклона отрезка [AB] к плоскости Н. [A₁’’B₁’’] = [AB].

Эту же задачу можно решить и заменой горизонтальной плоскости проекций Н на Н₁ (рис. 41). Новая плоскость Н₁ расположена перпендикулярно V и параллельно отрезку [AB], а новая ось х₁ || [AB]. Очевидно, что [A₁’B₁’] = [AB] и угол ⁰, образованный проекцией [A₁’B₁’] и осью х₁ равен углу наклона отрезка прямой [AB] к плоскости V.

Рис. 41

Задача 2. Преобразовать чертеж так, чтобы прямая общего положения оказалась перпендикулярной одной из плоскостей проекций новой системы.

Преобразование одной из проекций прямой общего положения в точку требует двойной замены плоскостей, так как в системе плоскость, перпендикулярная к прямой, не будет ортогональной ни к Н, ни к V.

При переходе от системы к системе плоскость V₁ располагают перпендикулярно Н и параллельно прямой [AB] (рис. 42), т.е. решают первую задачу, рассмотренную выше.

При второй замене новую плоскость Н₁ располагают перпендикулярно отрезку прямой [AB], т.е. х₂  A₁’’B₁’’. Этим самым будет обеспечено условие ортогональности V₁ и Н₁. Значение Y = const при этом берутся не из исходной системы , а из системы , которую мы преобразуем, т.е. из которой переходим в конечную систему . На плоскости Н₁ прямая изобразится точкой. Итак, в системе прямая стала проецирующей относительно плоскости Н₁.

Д

Рис. 42

анную задачу можно решить и заменой вначале плоскости Н на Н₁ и затем V на V₁ (рис. 43). Системы плоскостей проекций в рассмотренных случаях

претерпевают следующие

изменения:

- для рис. 42

- для рис. 43

Рис. 43

Задача 3. Преобразовать чертеж так чтобы плоскость общего положения в новой системе плоскостей проекций стала проецирующей.

Рис. 44

Пусть плоскость общего положения дана тремя точками А, В, С (рис. 44). Для решения поставленной задачи новую плоскость проекций необходимо расположить перпендикулярно АВС и одной из плоскостей проекций. Значит, новая плоскость проекций должна быть перпендикулярна какой-либо прямой, расположенной в заданной плоскости. В качестве такой прямой удобно взять любую горизонталь h плоскости треугольника АВС, направление которой заведомо известно. Расположением V₁  h (т.е. х₁  h’) обеспечиваются выполнение сразу двух условий: новая плоскость проекций V₁  H и V₁  АВС, поэтому новую ось х₁ проводим  h₁ (т.е.  A’1’). Проведя через горизонтальные проекции А’B’C’ вершин треугольника АВС, прямые, перпендикулярные новой оси откладываем на этих прямых от оси х₁ отрезки A_x1A_1­’’ = A_xA’’, B_x1B_1­’’ = B_xB’’, C_x1C_1­’’ = C_xC’’. Так получается новая фронтальная проекция А₁’’B₁’’C₁’’ треугольника АВС, представляющая собой прямую линию. На плоскость V₁, которая перпендикулярна треугольнику и Н без искажения проецируется угол ⁰, образованный треугольником и плоскостью проекции Н.

Аналогичное преобразование выполнению на рис. 45, где плоскость Н заменена плоскостью Н₁, перпендикулярной V и треугольнику АВС. Для этого в плоскости треугольника была проведена фронталь V = A1, перпендикулярно которой и располагается плоскость Н₁. Поэтому новая ось x₁ выбрана перпендикулярно v’’ = A’’1’’. Плоскость треугольника относительно Н₁ стала

Рис. 45

проецирующей. На плоскость Н₁ без искажения проецируется угол ⁰ наклона треугольника к фронтальной плоскости проекций V.

Задача 4. Преобразовать чертеж так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы.

Пусть дан треугольник АВС общего положения в системе . Нужно создать такую новую ортогональную систему плоскостей проекций, в которой одна из них должна быть параллельна треугольнику. В системе такую плоскость построить нельзя, поскольку плоскость, параллельная треугольнику, не будет перпендикулярна ни Н, ни V, т.е. она не образует с плоскостями проекций ортогональной системы.

Решение задачи требует двойной замены плоскостей проекций (рис. 46). Смысл первой замены заключается в преобразовании треугольника в проецирующую плоскость. Этот процесс описан выше (см. решение задач 44, 45).

Рис. 46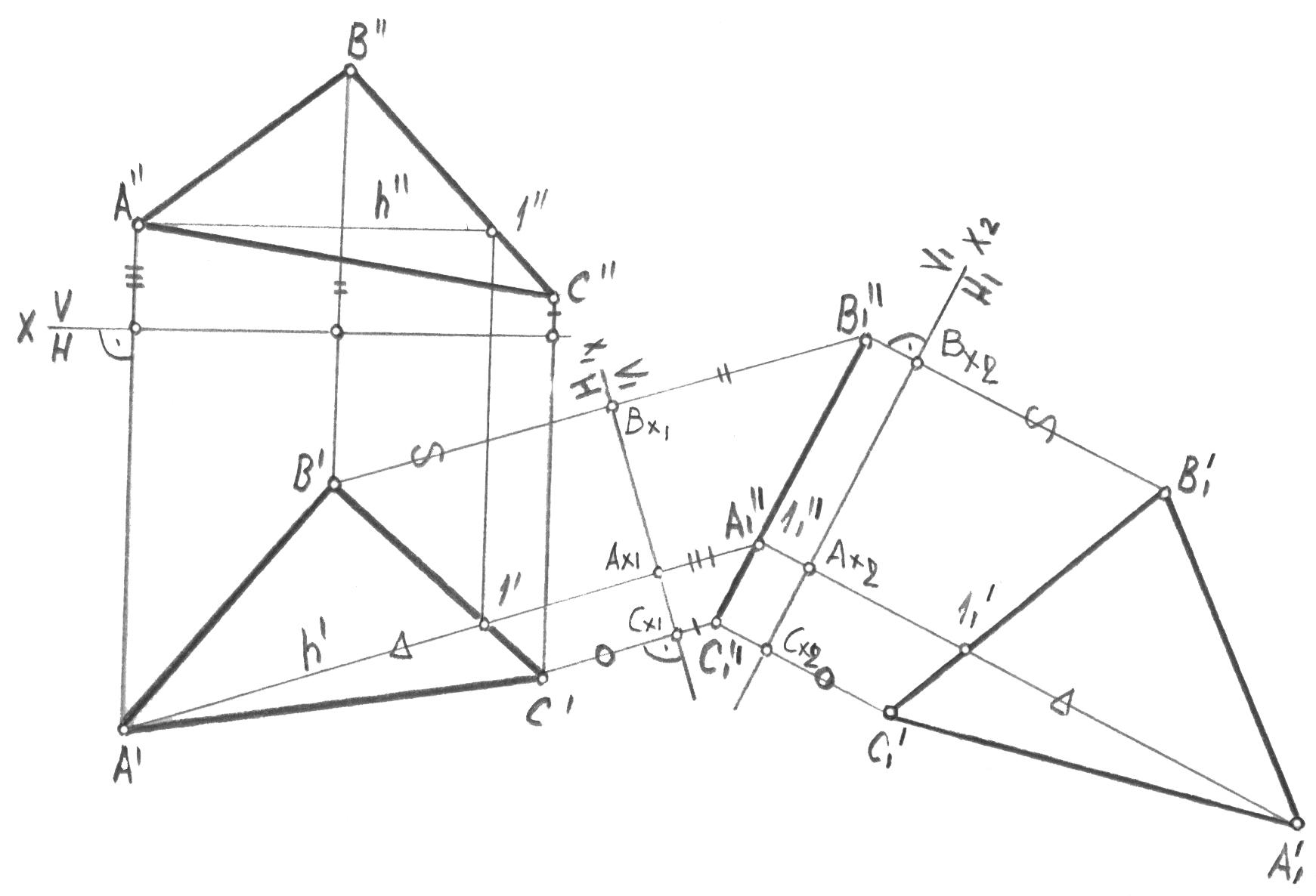

Второй этап решения задачи заключается в переходе от системы к системе при Y – const в системе (рис. 46).

Новая плоскость Н₁ устанавливается параллельно оси х₂, на перпендикулярах к которой откладываем расстояния В₁’B_x2 = B’B_x1, A₁’A_x2 = A’A_x1, С₁’С_x2 = С’С_x1 (значение координаты Y = const каждой точки в системе ). Построенная проекция A₁’B₁’C₁’ определяет истинную величину АВС.

Аналогично данную задачу можно решить двойной заменой системы плоскостей проекций.

(рис. 47)

С использованием метода перемены плоскостей проекций решаются также задачи на определение взаимной принадлежности геометрических фигур и построение поверхностей наперед заданной формы.

Рис. 47