3.4 Прямая и точка в плоскости

Задачи на принадлежность прямой и точки к плоскости в общем случае сводятся к двум типовым задачам.

Первая типовая задача. Плоскость  задана любым образом, например, двумя параллельными прямыми l || m (или их отрезками АВ, СD), рис. 29а. Провести любую прямую n, принадлежащую этой плоскости. Рассуждаем следующим образом. Прямая l принадлежит плоскости  всеми своими точками (ведь она задает эту плоскость), в том числе произвольной точкой 1 (см. 1’’  A’’B’’ и 1’  A’B’). Аналогично бесспорно доказываем, что точка 2 принадлежит CD (2’’  C’’D’’ и 2’  C’D’). Прямая n, проходящая через точки 1 и 2 принадлежит плоскости , так как проведена через две точки, принадлежащие этой плоскости (заметим, что таких прямых может быть проведено бесчисленное множество). Эта аксиома и является первым условием принадлежности прямой к плоскости.

Рис. 29а

Рис. 29б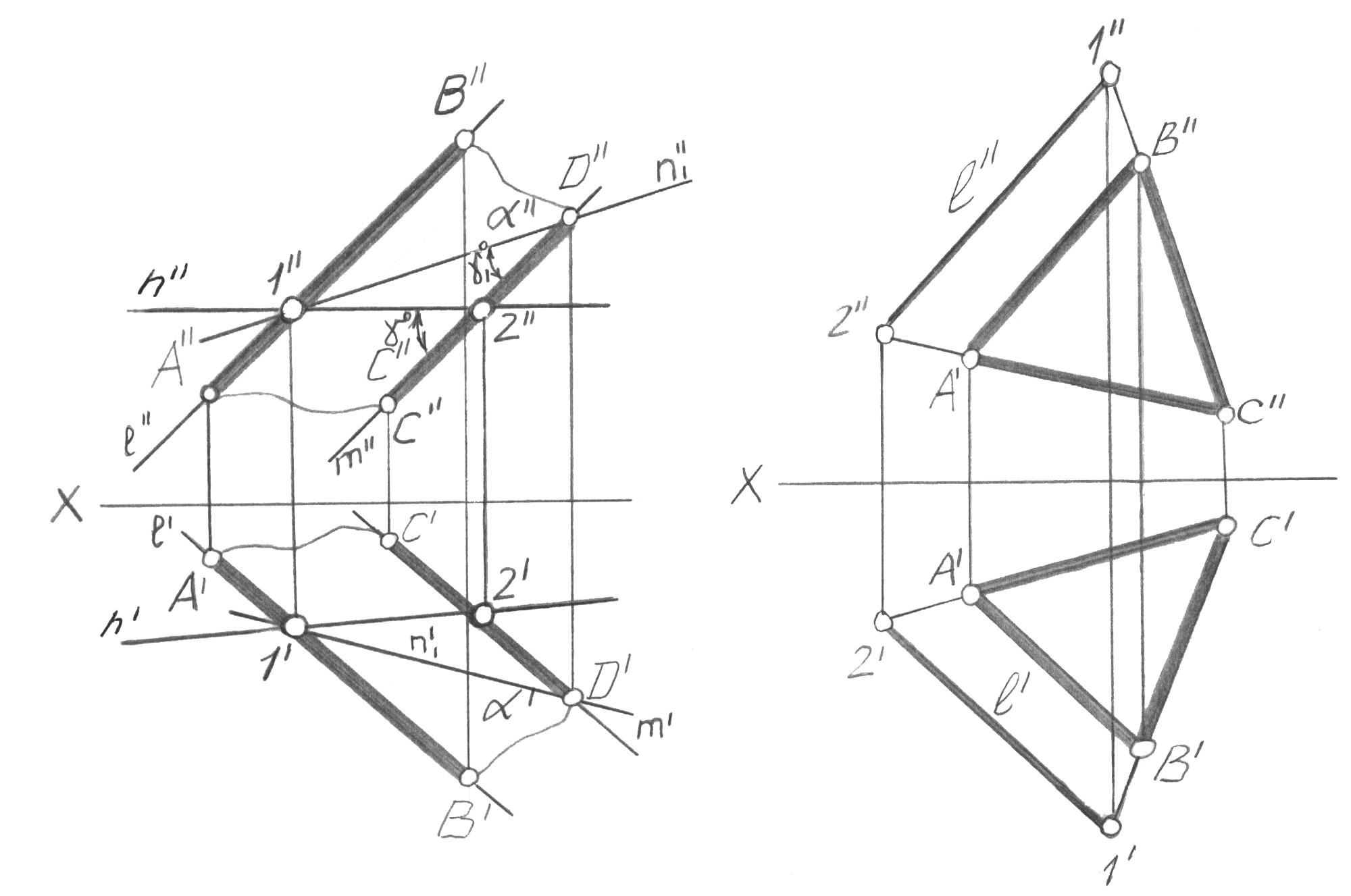

Теперь представим, что прямая n проходит через точку 1 прямой l и точку D прямой m, т.е. заняла положение n₁. Что произойдет с углом  между прямыми m и n? Этот угол уменьшится до величины ₁. Если точка D по прямой m уйдет в бесконечность, угол  (₁) уменьшится до нуля, т.е. прямая n станет параллельна m. Отсюда – второе условие принадлежности прямой к плоскости: прямая принадлежит плоскости, если проходит через одну точку (1) этой плоскости и параллельна какой-либо прямой (m) этой плоскости. Практическая реализация этого условия представлена на рис. 29б. Надеемся, Вы поняли, что плоскость здесь задана треугольником АВС. При этом пусть Вас не смущает, что проекции линии l находятся за пределами контура проекций треугольника: ведь плоскость безгранична в пространстве и искусственно ограничивается каким-то образом на чертеже (в нашем случае – треугольником АВС).

Вторая типовая задача. Плоскость  задана любым образом, например, треугольником АВС (рис. 30). Построить любую точку D, принадлежащую плоскости . Эта задача решается в два этапа. Первый – построить любую прямую l, принадлежащую плоскости  (см. выше). И второй этап – взять на этой прямой любую точку (в пределах контура треугольника АВС или за ним). Прямая l принадлежит плоскости , так как проходит через точки A и М (см. A’M’, A’’M’’) этой плоскости. На этой прямой l (см. l’, l’’) в любом месте взята точка D (см. D’D’’). Отсюда условие принадлежности точки плоскости: точка принадлежит плоскости, если находится на любой

Рис. 30 прямой этой плоскости. Если плоскость задана следами, то прямая принадлежит плоскости в том случае, когда следы прямой находятся на одноименных с ними следах плоскости (рис. 31) или прямая параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 32).

Рис. 31а

Рис. 31б

Рис. 32а

Рис. 32б

3.5 Главные линии плоскости

Через любую точку плоскости  в общем случае могут быть проведены 6 главных (замечательных) линий: горизонталь h, фронталь f или v, профиаль w и по перпендикуляру к каждой из них (расположенному тоже в этой плоскости), называемому линией наибольшего наклона или линией ската.

Горизонталь h – прямая, лежащая в плоскости  и параллельная горизонтальной плоскости проекции Н (рис. 33). Фронтальная проекция h’’ горизонтали, как линии с постоянным значением аппликаты z, параллельна оси х и расположена над нею.

Рис. 33а

Рис. 33б

Фронталь v – прямая, лежащая в плоскости  и параллельная фронтальной плоскости проекций V (рис. 34). Горизонтальная проекция v’ фронтали, как линии с постоянным значением ординаты Y, параллельна оси х и расположена под нею.

Рис. 34а

Рис. 34б

П

Рис. 35а

Рис. 35б

рофиаль (профильная прямая) w – прямая, лежащая в плоскости  и параллельная профильной плоскости проекции w (рис. 35). Горизонтальная w’ и фронтальная w’’ проекции профиали перпендикулярны оси х, как линии с постоянным значением абсциссы Х.

Линия наибольшего ската – прямая, лежащая в плоскости  перпендикулярно ее горизонталям h₀, h₁ … h_i (рис. 36). Аналогично строятся линии наибольшего наклона плоскости  к плоскостям проекций V и W.

Рис. 36а

Рис. 36б

Отметим, что все одноименные главные линии плоскости параллельны друг другу, следовательно параллельны между собой и их одноименные проекции. Следы плоскости тоже являются ее главными линиями с нулевыми значениями соответствующей координаты: горизонтальный след _H – это нулевая горизонталь (Z = 0), фронтальный след _V – нулевая фронталь (Y = 0) и профильный след – нулевая профиаль (X = 0).

С

Рис. 37

помощью главных линий плоскости удобно решать задачи на принадлежность точки (прямой) к плоскости. Например, плоскость  задана следами _V, _H. Даны проекции точки А (рис. 37). Следует определить, принадлежит ли точка А плоскости ? Исходим из того, что точка А действительно принадлежит плоскости . Тогда, во-первых, через нее можно провести горизонталь h (фронталь f) плоскости, направления проекций которой заведомо известны (для горизонтали h’’ || x и A  h’’). И во-вторых, горизонтальная проекция h’ горизонтали h (фронтали f) должна пройти через горизонтальную проекцию A’ точки А. Если этого не произойдет, как в нашем случае, точка А не принадлежит плоскости , так как не принадлежит горизонтали h этой плоскости.