Раздел 3. Проецирование плоскости

3.1 Задание плоскости

Плоскость является простейшей поверхностью. В общем случае плоскость в пространстве и на чертеже может быть задана одним из следующих способов:

а) тремя точками, не лежащими на одной прямой, или треугольником, если эти точки соединить отрезками прямых -  (А, В, С), рис. 17;

б) прямой и точкой вне ее -  (m, C), рис. 18;

в) двумя параллельными прямыми -  (m || n), рис. 19;

г) двумя пересекающимися прямыми -  (m ∩ n), рис. 20;

д) плоской фигурой  (’’, ’), рис. 21;

е) следами -  (_V, _H), рис. 22.

Рис. 17

Рис. 18

Рис. 19

Рис. 20

Нетрудно увидеть, что способы «б», «в», «г» легко сводятся к способу «а», т.е. в сущности, представляют один и тот же способ со своими разновидностями. Задания же плоскости следами требует отдельного рассмотрения.

Рис. 21

3.2 Следы плоскости

Следом плоскости  называется линия ее пересечения с плоскостью проекций. Плоскость, не параллельная и не перпендикулярная ни одной плоскости проекций, обязательно где-то пересечет каждую из плоскостей проекций. Следовательно, такая плоскость имеет 3 следа, по числу плоскостей проекций (H, V, W), рис. 22а. На нем _V, _H, _W – соответственно фронтальный,

Рис. 22а

Рис. 22б

горизонтальный и профильный следы плоскости _­, а точки А_X, А_Y, A_Z – точки схода следов. При переходе к эпюру Г. Монжа получим изображение, показанное на рис. 22б. Поскольку элементарный геометрический объект совершенно однозначно задается любыми проекциями, профильный след _W вместе с осями z и y и точками _Z, _Y можно удалить.

3.3 Классификация плоскостей

По положению в пространстве различают плоскости общего положения, не параллельные и не перпендикулярные ни одной из плоскостей проекций, и плоскости частного положения. В свою очередь, плоскости частного положения подразделяются на проецирующие (перпендикулярные только одной плоскости проекций) и уровня (перпендикулярные сразу двум плоскостям проекций и, следовательно, параллельные третьей плоскости проекций, по отношению к которой и дается название плоскости).

3.3.1 Проецирующие плоскости

П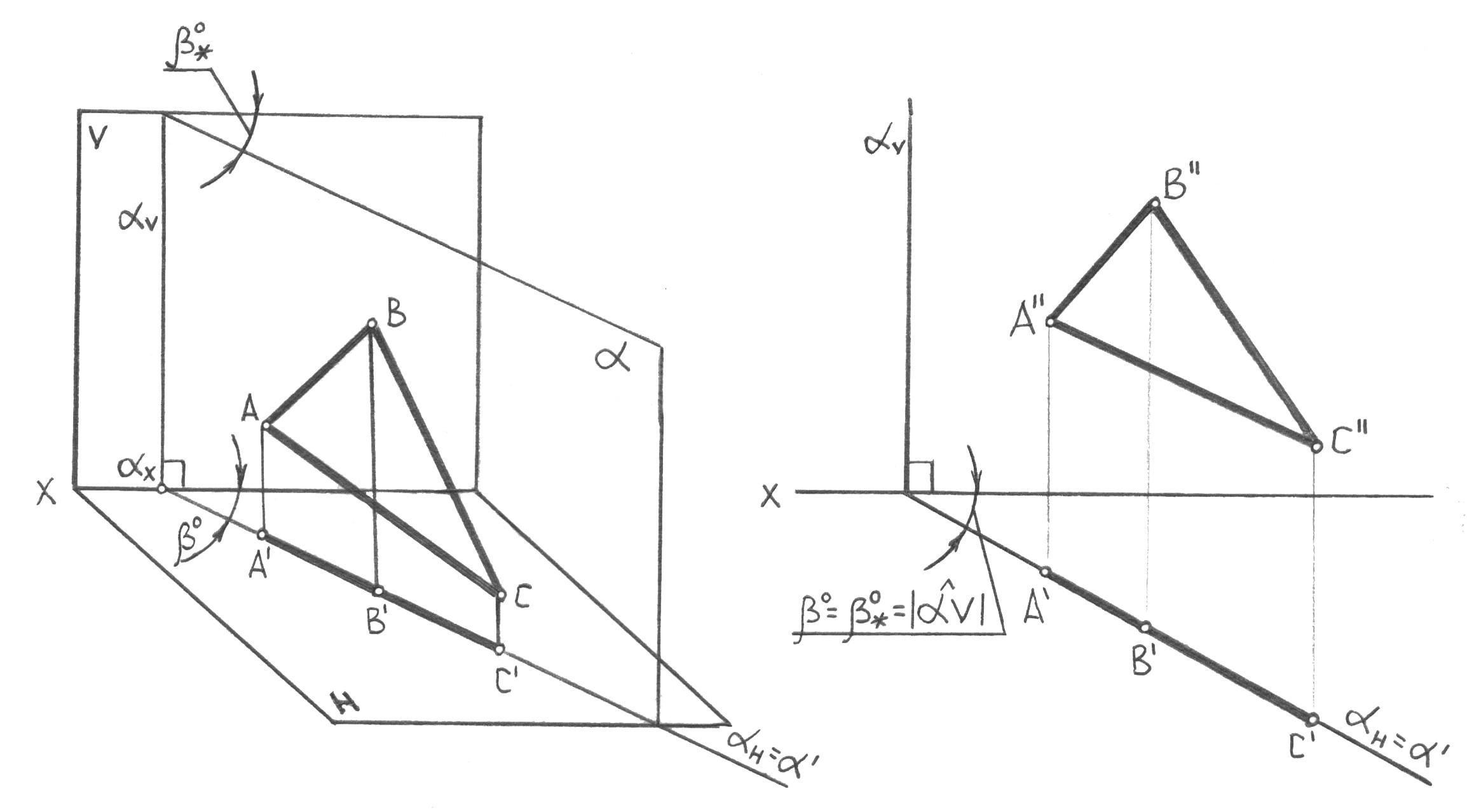 лоскость, перпендикулярная горизонтальной плоскости проекций называется «горизонтально-проецирующая» (рис. 23). Ее фронтальный след _V

Рис. 23а

Рис. 23б

перпендикулярен к оси х, а горизонтальный след _Н может занимать произвольное положение, но не перпендикулярное к оси х. На эпюре (рис. 23б) угол β⁰ наклона горизонтального следа _Н к оси х есть действительная величина угла β⁰_* наклона плоскости  _к фронтальной плоскости проекций.

Любая точка (или А, или В, или С), прямая (или АВ, или ВС, или АС) или плоская фигура (АВС), расположенные в горизонтально-проецирующей плоскости, отображается на ее горизонтальном следе _Н. Поскольку таких точек на плоскости   Н может быть взято бесконечное множество, ее горизонтальный след _Н по сути одновременно является горизонтальной проекцией всех ее точек и, следовательно, самой плоскости. Поэтому _Н носит двойное название «след-проекция» и двойное обозначение _Н = ’. В заключение отметим, что на рис. 23а фронтальные проекции точек АВС не показаны, чтобы не загромождать изображение несущественной для данного случая информацией, хотя реально эти проекции, бесспорно, существуют.

Плоскость, перпендикулярная фронтальной плоскости проекций, называется «фронтально-проецирующая» (рис. 24). Ее горизонтальный след _Н перпендикулярен оси х, а фронтальный след – проекция может занимать

Рис. 24а

Рис. 24б

произвольное положение, не перпендикулярное оси х. Расположенные в ней любые плоские объекты отображаются на ее фронтальном следе – проекции _V = ’’. Наклон _V = ’ к оси х – есть действительная величина угла β⁰_* наклона плоскости  к горизонтальной плоскости проекций Н.

П

Рис. 25а

Рис. 25б

лоскость, перпендикулярная профильной плоскости проекций, называется «профильно-проецирующая» (рис. 25). Расположенный в ней плоский объект отображается на профильный след-проекцию _W = ’’’ (А’’’B’’’C’’’), а трехплоскостное изображение (для данного случая) позволяет указать углы β и  наклона этой плоскости соответственно к горизонтальной и фронтальной плоскостям проекций.

3.3.2 Плоскости уровня

Плоскость, параллельная горизонтальной плоскости проекций и, следовательно, перпендикулярная фронтальной и профильной плоскостям проекций, называется «горизонтальная плоскость уровня» (рис. 26). Ее фронтальный и не показанный на рис. 26 профильный следы-проекции занимают горизонтальное положение, а горизонтальный след отсутствует. Плоская фигура АВС, расположенная в горизонтальной плоскости , на V и W отображается отрезками прямых, а на Н – треугольником действительной величины.

Для фронтальной плоскости уровня (рис. 27) горизонтальный след-проекция параллельны оси z, а фронтальный след отсутствует. Находящийся в

Рис. 26а

Рис. 26б

ней треугольник АВС на фронтальную плоскость проекций отображается в действительную величину.

Р асположенная в профильной плоскости уровня плоская фигура (рис. 28) на профильную плоскость проекций отображается в действительную

Рис. 27а

Рис. 27б

Рис. 28а

Рис. 28б

величину, а на фронтальный и горизонтальный следы-проекции – отрезками прямых.