3. Практическая часть.

Выполнение задания необходимо начать с построения зависимости состава пара от состава жидкости для смеси метанол-вода. На основании опытных данных (табл.1) в координатах х-у строим кривую равновесия для смеси метанол-вода при атмосферном давлении и кривые температур кипения и конденсации.

Таблица 1: Температуры кипения и конденсации системы метанол-вода.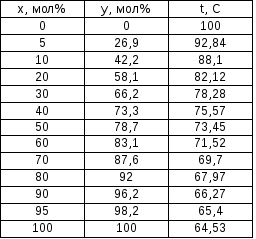

.

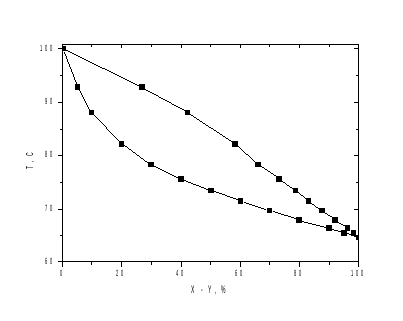Рисунок 1: Изобары температур кипения и конденсации системы метанол-вода.

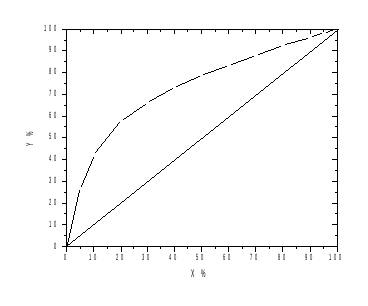Рисунок 2: Зависимость равновесных концентраций.

Для того, чтобы определить в какой степени система метанол-вода отклоняется от идеального поведения необходимо провести расчет для идеальной системы. Для идеальной системы Y-X диаграмму можно описать аналитически, исходя из того, что раствор атермален – образуется за счет энтропийного фактора. Тогда, согласно закону Рауля:

,

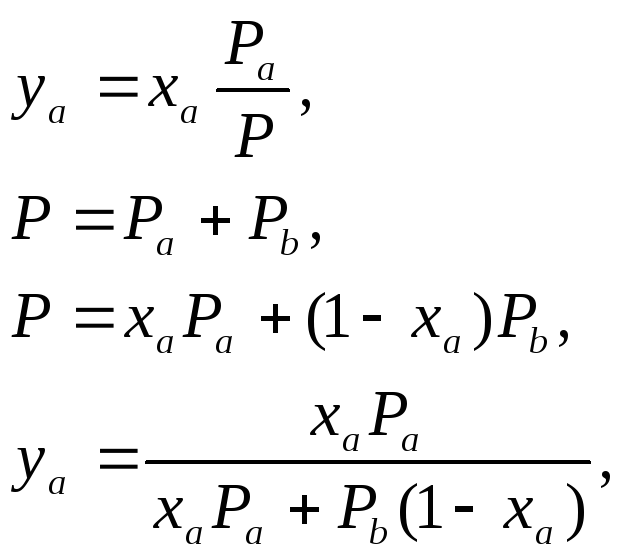
г

Таблица 2: К расчету относительной летучести.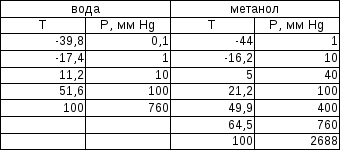

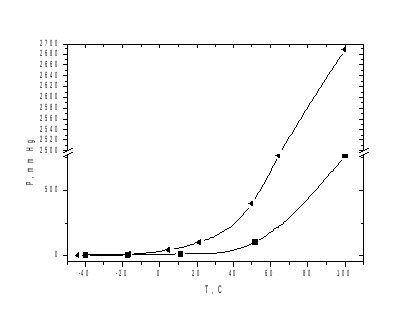
де R – относительная летучесть, которая рассчитывается как отношение давлений насыщенных паров компонентов: .

Рисунок 3: Зависимость давления насыщенного пара от температуры для воды (снизу) и метанола (сверху)

Так как парциальные давления меняются не пропорционально, то для расчета берут среднее геометрическое при краевых значениях температуры, фигурирующих в Т-X диаграмме.

При Т=64,5⁰С:

При Т=100⁰С:

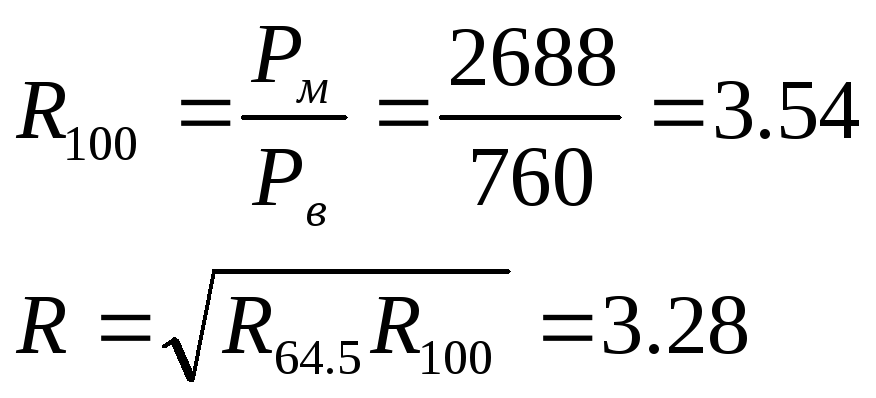
Тогда, принимая R=3.28 можно построить расчетную Y-X зависимость и, сравнивая ее с экспериментальной кривой, показать, что при высоких концентрациях поведение системы идеально, а при низких концентрациях поведение системы отклоняется от идеального, что изображено на рис. 4:

Рисунок 4: Идеальная (снизу) и реальная (сверху) зависимости равновесных концентраций.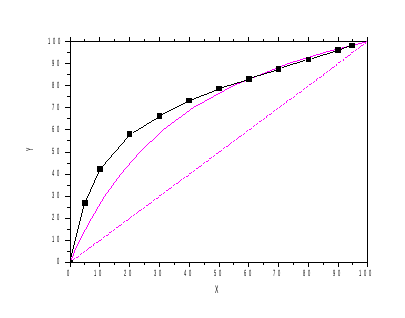

Линейное отклонение достигает 74.32% при высоких количествах легколетучего компонента, а при содержаниях легколетучего компонента менее 40% поведение системы не отличается от идеального.

Таблица 3: К расчету отклонения системы от идеального поведения.

Состав пара
Метанол-вода	Ид. Раствор	Отклонение
26,41	15,15	74,32
41,32	28,21	46,47
58,44	45,79	27,62
65,64	59,32	10,65
73,33	68,37	7,25
78,69	76,03	3,49

Для расчета состава кубового остатка и среднего состава дистиллята после простой постепенной перегонки одной трети объема исходной эквимольной смеси и при изменении соотношения дистиллят — кубовый остаток необходимо оценить значение интеграла .

Для этого строим зависимость от x и подбираем для этой зависимости соответствующую интерполяционную зависимость.

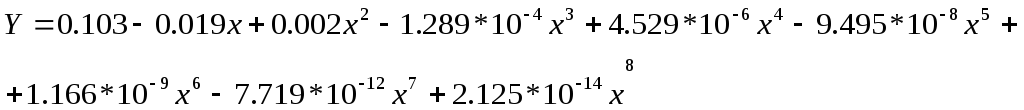
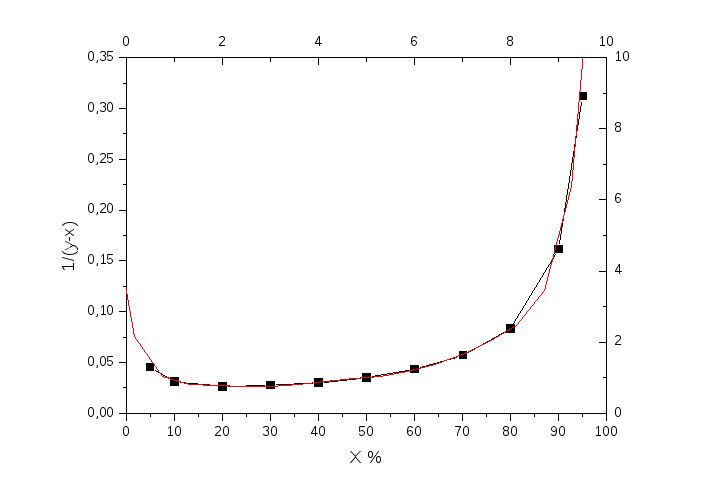
Рисунок 5: Для оценки значения интеграла.

С помощью этой зависимости оценим x_w – состав кубового остатка. Для этого обратимся к следующей таблице. Для того чтобы оценить состав кубового остатка и средний состав дистиллята необходимо проинтегрировать интерполяционную зависимость, указанную выше, в пределах от x_f до x_w. Получим значения, указанные в графе ln(F/W). Далее потенцируем полученные результаты и, исходя из того, что , находим W и P – конечное количество разделяемой смеси и количество получаемого дистиллята соответственно. Исходя из этого, находим средний состав дистиллята.

Рисунок 6: Расчет состава кубового остатка и среднего состава дистиллята.

Xw, %	Xf, %	ln(F/W)	F/W	F	W	P	Xp, %
1	50	1,58	4,85	1,00	0,21	0,79	62,72
5	50	1,33	3,78	1,00	0,26	0,74	66,19
10	50	1,15	3,15	1,00	0,32	0,68	68,60
15	50	1,00	2,73	1,00	0,37	0,63	70,27
20	50	0,87	2,38	1,00	0,42	0,58	71,74
25	50	0,74	2,09	1,00	0,48	0,52	73,02
30	50	0,60	1,83	1,00	0,55	0,45	74,08
35	50	0,47	1,60	1,00	0,63	0,37	75,05
37,245	50	0,41	1,50	1,00	0,67	0,33	75,51
40	50	0,32	1,38	1,00	0,72	0,28	76,13
45	50	0,16	1,18	1,00	0,85	0,15	78,04

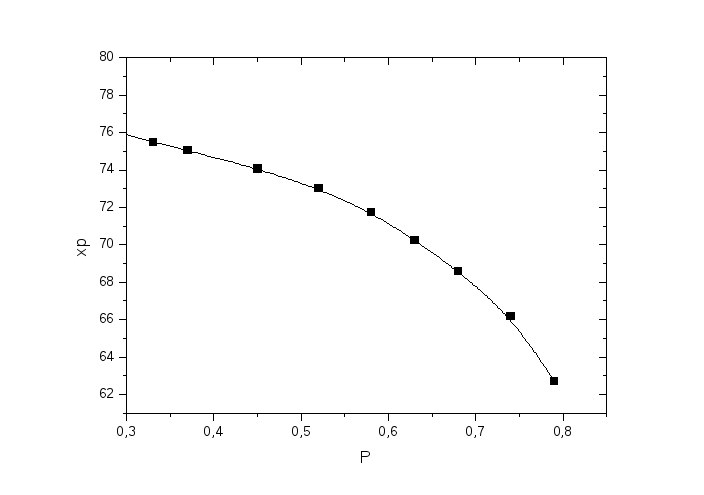
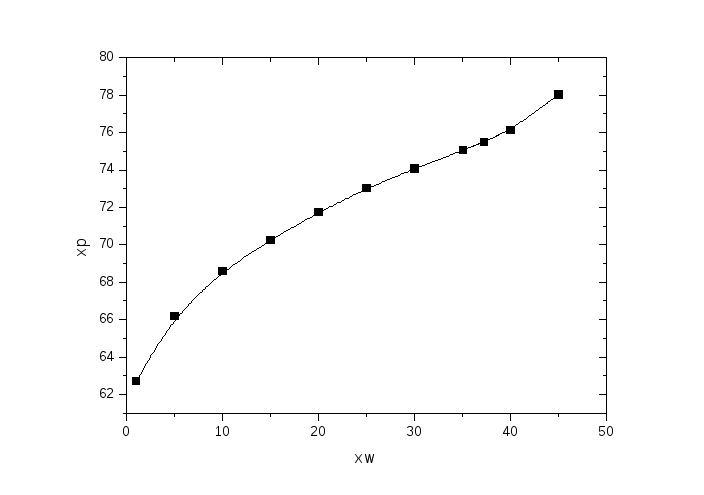
Рисунок 6: Зависимости среднего состава дистиллята от количества дистиллята (сверху) и от состава кубового остатка (снизу).

По графику видно, что чем больше кубового остатка, то есть чем меньше перегоняемый объем, тем лучше средний состав дистиллята. Зависимость среднего состава дистиллята от составов первой и последней фракции практически линейна, наблюдаемые отклонения могут быть обусловлены точностью вычислений. Также можно сказать, что существуют области параметров, корректное описание которых невозможно провести, опираясь только на данные расчета. Это области составов, близких к исходному эквимольному составу системы.