Формула литтла

Среднее время пребывание заявки в системе определяется теоремой Литтла:

Для любой системы массового обслуживания, при любом характере потока заявок, при любом распределении времени обслуживания и при любой дисциплине обслуживания среднее время пребывания заявки в системе (T_сист) в стационарном режиме равно среднему числу заявок в системе (K_сист), деленному на интенсивность потока заявок [4 ].

Отметим, что время пребывания в системе заявки, получившей отказ в обслуживании, оказывается равным нулю.

Доказательство. Пусть на вход системы массового обслуживания поступает поток заявок с интенсивностью . Полагаем, что система функционирует в стационарном режиме достаточно длительное время T (T>>1/).

За время T на вход системы поступает nT заявок, каждая из которых находится в системе время t_i (i=1..n). В число n входят и заявки, получившие отказ в обслуживании. Время их пребывания в системе полагается равным нулю.

Суммарное время пребывания всех заявок в системе

.

Очевидно, что среднее число заявок в системе в течение времени T

K_сист=T_сумм/T.

Если числитель и знаменатель правой части равенства умножить на , то

.

Но отношение t_i/n есть ни что иное, как среднее время нахождения одной заявки в системе:

.

Откуда следует так называемая формула Литтла

Tсист=Kсист/.

При конечном числе каналов (n) и мест для ожидания (m) число заявок, которые могут находиться в системе, ограничено величиной

n+m. Поэтому с увеличением интенсивности входящего потока среднее время пребывания заявки в системе сначала растет (по мере заполнения каналов обслуживания и мест в очереди заявками), а затем вследствие возрастания вероятности отказа в обслуживании начинает уменьшаться так, что асимптотически при 

T_сист  (n+m) /.

Аналогичное равенство в большинстве случаев верно и для среднего времени ожидания заявки в очереди

T_ож=K_ож/,

где K_ож - среднее число заявок в очереди [4]. Отметим, что для некоторых систем это соотношение может оказаться неверным (в частности, для некоторых систем с инверсным, начиная с конца очереди, обслуживанием заявок [5]).

Одноканальные системы массового обслуживания

5.1. Системы m/m/1

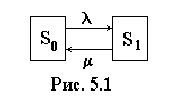
Заявка, пришедшая в момент, когда канал занят, теряется. Множество возможных состояний системы: S₀ - канал обслуживания свободен и S₁ - канал занят. Граф состояний системы изображен на рис. 5.1. Уравнения Колмогорова:

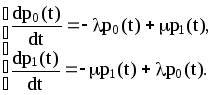
Уравнение нормировки

.

Для решения системы уравнений воспользуемся уравнением нормировки и исключим из первого уравнения p₁(t):

.

Предельная вероятность состояния S₀ p₀=/(+). Характеристическое уравнение r+(+)=0 имеет корень r= -(+).

Найдем решение дифференциального уравнения при начальных условиях p₀(0)=1, p₁(0)=0.

Общее решение уравнения

p₀(t)=C₁+C₂exp[-(+)t],

где C₁, C₂ - постоянные интегрирования, которые определяются из условий:

- при t предел lim _t[dp₀(t)/dt] =0 и C₁=p₀=/(+);

- при t=0 C₁+C₂=1, откуда С₂=/(+).

Вероятности состояний

,

.

Предельные вероятности

.

Показатели эффективности системы.

Относительная пропускная способность в стационарном режиме

q=/(+).

Абсолютная пропускная способность в стационарном режиме может быть определена, исходя из следующего:

- если бы канал обслуживания был занят непрерывно, то была бы реализована максимальная для данной системы абсолютная пропускная способность , равная  (заявок в единицу времени);

- канал обслуживания занят с вероятностью , следовательно,

Вероятность отказа в обслуживании P_отк=p₁.

Среднее число связанных с системой заявок K_сист=p₁=/(+).

Среднее время нахождения заявки в системе (по формуле Литтла)

.

Среднее время нахождения заявки в системе оказывается меньше среднего времени обслуживания (1/) вследствие того, что некоторые из заявок получают отказ и время их нахождения в системе оказывается равным нулю. При  T_сист 1/.

****************************************************************