25

В.Н. Донцов

член-корр. МААН, доцент ВГУ, канд. педагог. наук

Проект урока математики

Дата:___________ .

Предмет: «Алгебра и математический анализ: 10 - 11 классы».

Профильный класс: 10-11 с углубленным изучением математики.

Тема: «Методы решения иррациональных уравнений (их таксономия)».

Эпиграф урока:

«Решение задач – практическое ис - кусство, подобное плаванию, катанию на лыжах или игре на фортепиано. Научиться ему можно, только подражая хорошим образцам и постоянно практикуясь». (Дьердь Пойя (1887 - 1985) )

Цель и психолого-педагогические задачи урока (сдвоенного):

Ι. Общеобразовательная (нормативная) цель (на этапе подготовки к ЕГЭ, ЦТ): на материале одного задания выборочно повторить и закрепить некоторые методы решения иррациональных уравнений по методическому принципу смены приоритетов: «нахождение идей решения и/или получение ответа» (В.И. Арнольд, М.И. Башмаков, А.А. Деркач, Г.В. Дорофеев, Ю.М. Колягин, Н.В. Кузьмина, Ю.М. Макарычев, Н.Г. Миндюк, А.Г. Мордкович, С.М. Никольский, М.К. Потапов, В.А. Сластёнин, А.А. Окунев, А.Р. Рязановский, Н.Н. Решетников, И.Ф. Шарыгин, А.В. Шевкин).

ΙΙ. Задачи математического развития учащихся: на нестандартном учебно-математическом материале продолжить развитие ментального опыта учащихся, содержательной когнитивной структуры их математического интеллекта, в том числе, способностей к логико-дедуктивному и индуктивному, аналитическому и синтетическому обратимому мышлению (Ж. Пиаже, В.А. Крутецкий ), к алгебраическому и образно-графическому мышлению (В.И. Арнольд, А.Г. Мордкович, Г.В. Дорофеев, И.Ф. Шарыгин), к содержательному обобщению и конкретизации (В.В. Давыдов, Л.В. Занков), к рефлексии и самостоятельности как метакогнитивной способности (Р. Стернберг, М.А. Холодная) школьников; продолжить развитие культуры устной и письменной речи как психологических механизмов учебно-математического интеллекта.

III. Воспитательные задачи: продолжить личностно ориентированное воспитание у школьников познавательного интереса к математике, ответственности, чувства долга, академической самостоятельности, коммуникативного умения сотрудничать с классом, учителем, соклассниками; аутогогической способности к соревновательной учебно-математической деятельности, стремления к высоким и высшим её результатам (акмеический мотив).

Тип урока: по критерию ведущей цели – урок повторения, закрепления, таксономии методов решения иррациональных уравнений на основе деятельностного подхода в обучении; по критерию ведущего дидактического метода – урок эвристической беседы, урок проблемного воссоздания методов решения иррациональных уравнений; по критерию ведущего матема-

тического содержания – урок одной задачи (одного уравнения), урок – практикум; по критерию типа информационного взаимодействия учащихся и учителя – урок сотворчества, сотрудничества и соревновательности.

Оборудование урока:

1. Учебная литература:

   1. Виленкин Н.Я. Алгебра и математический анализ для 11 класса: учеб пособие для учащихся шк. и классов с углубл. изуч. курса математики /Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд – М.: Мнемозина, 2001. – С.111-114;

   2. Задачи повышенной трудности по алгебре и началам анализа: учеб. пособие для 10-11 кл. сред. шк. /Б.М. Ивлев [и др.]. – М.: Просвещение, 1990. – С.19-20.

2. Экран, мультимедийный проектор, 4 слайда, подготовленные в компьютерной системе «Mathematica-5».

Ход урока

I этап урока. Объявление темы и главной образовательной цели урока; стимулирование чувства долга, ответственности, познавательного интереса учащихся при подготовке к ЕГЭ и ЦТ.

II этап урока. Оценка качества и коррекция уровня выполнения домашней работы. Ответы на вопросы учащихся. Экспресс-контроль самостоятельных решений следующих иррациональных уравнений:

1. ( Решение методом перехода к системе уравнений относительно новых переменных. Ответ: );

2. ( Решение на основе теоремы о корне. Ответ: );

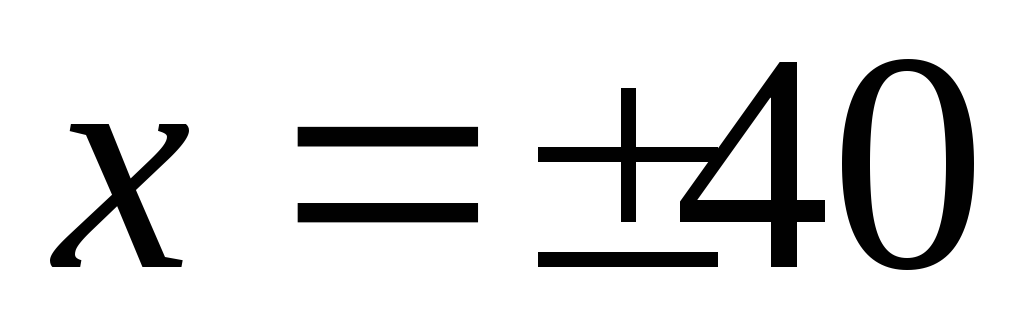3. ( Решение на основе использования монотонности функции. Ответ:).

Методические указания для начинающего учителя. Приведём возможные решения указанных заданий.

1. Решение уравнения :

Введём в рассмотрение две новые переменные:

, (1)

. (2)

Тогда u+v=4. Так как х+41= u⁴, 41 – х = v⁴ , то, сложив почленно эти два равенства, получим: u⁴+ v⁴=82. Для нахождения u и v имеем систему

(3)

Её решим, используя двукратно формулу a²+b²=(a+b)² – 2ab. Из равенства следует, что (u²+v²)² – 2u²v²=82, то есть ((u+v)² – 2uv)² – – 2u²v²=82. С учетом того, что , получаем (16 – 2uv)² – 2u²v²=82 256 – 64uv+4u²v² – 2u²v² – 82=0 2u²v² – 64uv+174=0

(uv)² – 32(uv)+87=0. По теореме, обратной теореме Виета, получаем, что uv=3 или uv=29. Поэтому система (3) равносильна следующей совокупности двух систем:

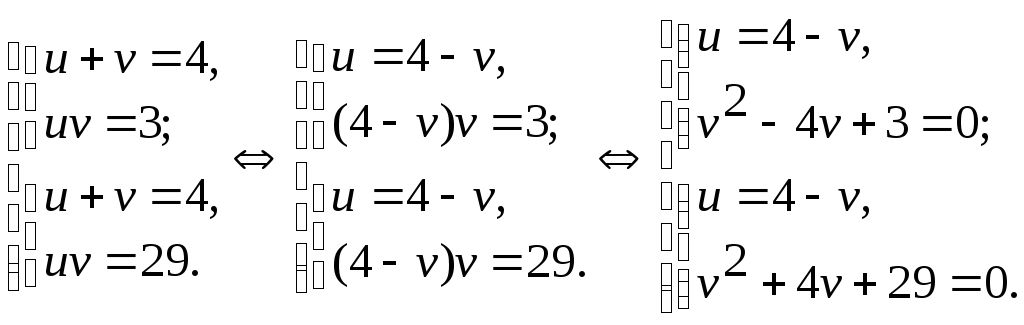
Вторая система последней совокупности решений не имеет, так как в уравнении дискриминант D<0. Значит, она равносильна следующей совокупности:

или

Возвращаясь к x, получаем:

Ответ: 40.

2. Решение уравнения :

Введём в рассмотрение функцию f(y)=. Тогда исходное уравнение можно представить в виде f(2x+1)+f(x)=0 f(2x + 1) = – f(x).

Заметим, что функция f(y) является нечётной на R, поэтому последнее уравнение можно переписать так: f(2x + 1) = f ( – x). (4)

Кроме того, она монотонно возрастает на всей своей области определения. Действительно, её производная положительна на R:

f ^/(y)=>0.

Поэтому на основании достаточного условия монотонности функция f(y) возрастает на R. В силу теоремы о корне из уравнения (4) следует, что

2х + 1 = – х .

Ответ: .

3. Решение уравнения .

Перепишем уравнение в виде . Введём в рассмотрение функцию f(x)=1+. Тогда полученное уравнение примет вид f(f(x))=x.

Для решения уравнений такого вида можно применить следующее

Утверждение. Если функция f(x) непрерывна и монотонно возрастает на промежутке X, то уравнения f(x)=x и f(f(x))=x равносильны на X.

Введённая в рассмотрение непрерывная функция f(x)=1+ монотонно возрастает при x 0. В соответствии с приведённым утверждением имеем: f(x)= x 1+=х

Ответ: .

ΙΙΙ этап урока. Деятельностный подход в систематизации методов решения иррациональных уравнений типа (*).

Методические указания для начинающего учителя. Принцип смены приоритетов при эвристическом диалоге, связанном с фронтальным повторением и обсуждением по выбору учащихся восьми методов решения иррациональных уравнений, предполагает:

1. повторение (устно/полуписьменно) стержневых идей и логики операционального состава того или иного метода;

2. письменное решение уравнения с целью получения точного окончательного ответа при реализации другого метода;

3. сравнение методов решений по таким критериям, как:

   1. оригинальность - традиционность идеи,

   2. объём логических аргументаций и вычислений,

   3. реализация внутри-, межпредметных связей,

   4. скорость получения ответа, затраты учебного времени,

   5. эстетическая привлекательность метода,

   6. распространенность метода в задачном материале;

   7. составление таксономии задач по методам их решения (деятельностный подход).

Приведем все 8 способов решения.