14.2. Свободные колебания. Математический и пружинный маятники.

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Рассмотрим свободные колебания математического и пружинного маятников и найдем уравнения, описывающие их колебательное движение.

Математическим маятником называют тело, подвешенное на тонкой нити при следующих условиях:

• Размеры тела значительно меньше длины нити,

• Нить невесомая и нерастяжимая,

• Силы сопротивления отсутствуют,

• Угол отклонения маятника от вертикали не превышает15⁰

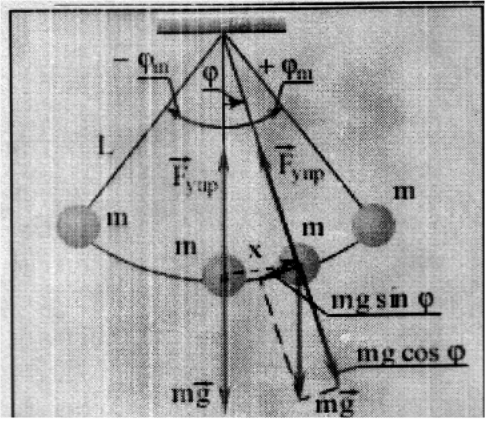
Рис. 14.4. Математический маятник. - угловое отклонение маятника от положения равновесия. x= l - смещение маятника по дуге

Если обозначить через х линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно = x/l. Для проекций векторов ускорения и силы на направление касательной второй закон Ньютона имеет вид :

где - возвращающая сила, направление которой противоположно направлению смещения. Возвращающая сила пропорциональна не смещению, а sin( x/l), и колебания будут гармоническими только при малых угловых смещениях , когда величина sin(x/l) отличается от x/l не более чем на 2%.

Для второго закона Ньютона при малых колебания маятника получаем

14.7

Для гармонических колебаний . Подставляя в (14.7) получаем , тогда собственная частота колебаний математического маятника выражается формулой

14.8

Так как период колебаний и циклическая частота связаны между собой (формула 14.4), то для периода свободных колебаний математического маятника получаем

14.9

Зависимость смещения от времени для математического маятника имеет вид:

14.10

В случае пружинного маятника возвращающей является сила упругости F_упр.

Рис. 14.5. Колебания груза на пружине без трения. Груз массой m прикреплен к пружине жесткости k . Второй конец пружины закреплен неподвижно.

Если пружина невесомая, деформация пружины упругая, трение отсутствует, то пружинный маятник будет совершать гармонические колебания. Циклическая частота свободных колебаний груза на пружине находится из второго закона Ньютона:

, но

Откуда

14.11

Период Т гармонических колебаний груза на пружине равен

14.12

При горизонтальном расположении системы пружина-груз сила тяжести , приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину х₀, равную

и колебания совершаются около этого нового положения равновесия. Выражения для собственной частоты и периода колебаний Т справедливы и в этом случае.

Так как ускорение является второй производной координаты тела х₀ по времени t

,

то второй закон Ньютона для груза на пружине имеет вид:

,

или

, 14.13

где

Решением уравнения (14.13) является гармоническая функция вида или . При видно, что при t=0 cos = 1, и это решение соответствует случаю, когда в начальный момент времени груз был выведен из положения равновесия на х_m, после чего стали происходить его колебания. Второй вид решения соответствует случаю, когда в начальный момент времени тело находилось в положении равновесия, и колебания возникли после того, как грузу сообщили скорость v_0. Если грузу, находящемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость v₀ . то амплитуда колебаний равна

В любой момент времени смешение для пружинного маятника описывается гармонической функцией вида

14.14