14. Механические колебания и волы
14.1 Гармонические колебания
Многие механизмы используют колебательное движение, например, сортировочные машины, отбойные молотки, часы, виброуплотнители и т.д.. Колебания могут вызывать вредные последствия, например, около 80% поломок в авиации и машиностроении являются следствием недопустимых колебаний.
При механических колебаниях тела обязательно взаимодействуют между собой. Например, при колебаниях груза на упругой нити взаимодействуют нить и груз, а при колебаниях пружинного маятника взаимодействуют пружина и груз. Взаимодействующие тела образуют колебательную систему. Для совершения колебаний необходимо, чтобы эта система обладала следующими свойствами:
-
Наличием состояния устойчивого равновесия
-
Появлением силы, возвращающей колебательную систему в состояние устойчивого равновесия, после того, как она из него выведена. Для груза на упругой нити возвращающая сила – это равнодействующая силы тяжести и силы натяжения нити. Для пружинного маятника возвращающая сила – это упругая сила.
-
При наличии сил сопротивления груз должен обладать достаточной инерцией, чтобы не останавливаться в положении устойчивого равновесия, а пройти за него.
Таким образом, колебательным называется движение тела относительно положения устойчивого равновесия, при котором возникающая в результате взаимодействия тел колебательной системы сила возвращает тело к положению устойчивого равновесия.
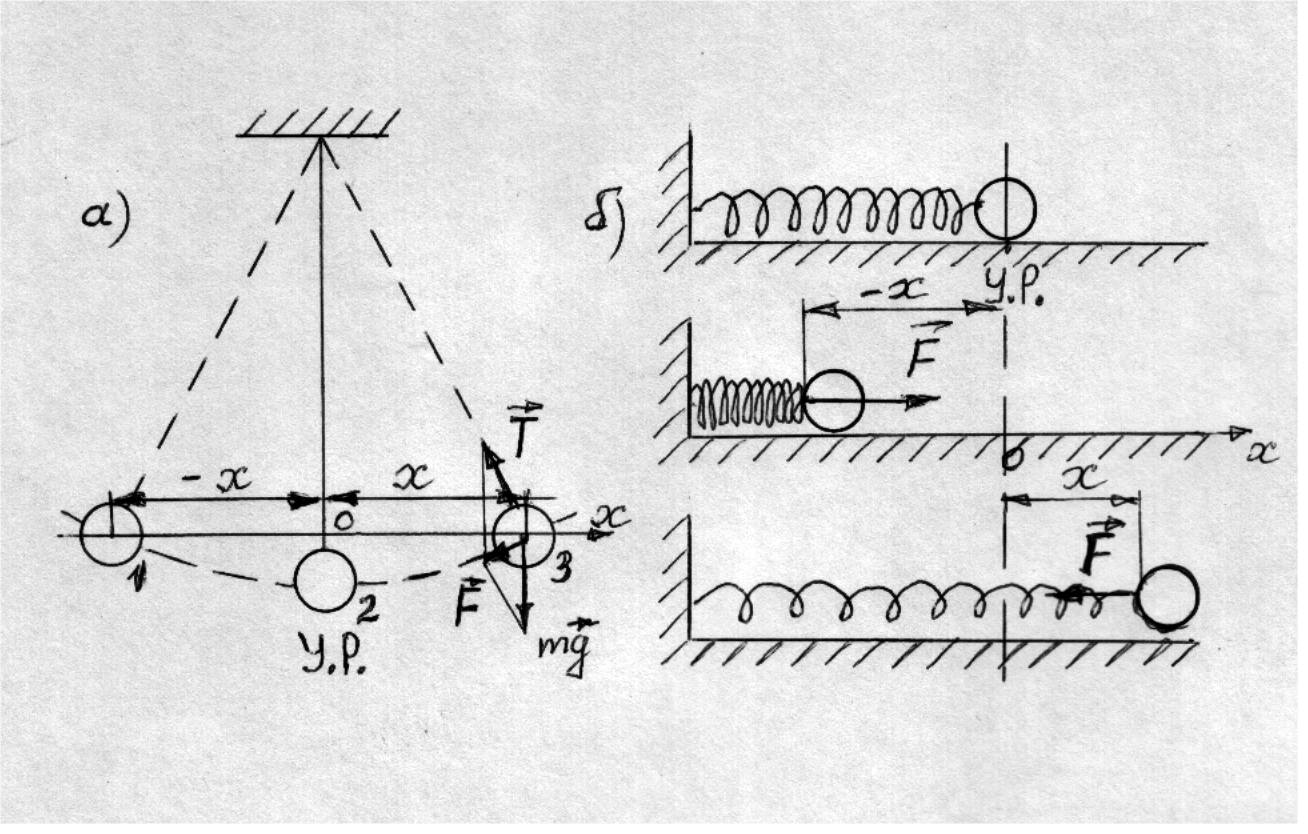
Рис. 14.1. Колебания груза на упругой нити (а) и пружинного маятника (б). F – возвращающая сила.
У.Р. – положение устойчивого равновесия.
Для описания колебательного движения могут быть использованы знания, полученные при описании движения точки по окружности. Проекция на ось координат точки, движущейся по окружности, совершает колебательное движение, рис.14.2. Промежуток времени, через который колебательная система возвращается в исходное положение, то есть совершает одно полное колебание, называется периодом колебаний и обозначается Т. По окружности за это время материальная точка проходит один оборот. Если за время t произошло N полных колебаний, то
, 14.1
Число полных колебаний, совершаемых системой за одну секунду, называется частотой колебаний. Если за время t совершено N полных колебаний, то
, 14.2
Частота колебаний измеряется в герцах. 1Гц – это частота колебаний, при которых за одну секунду совершается одно полное колебание
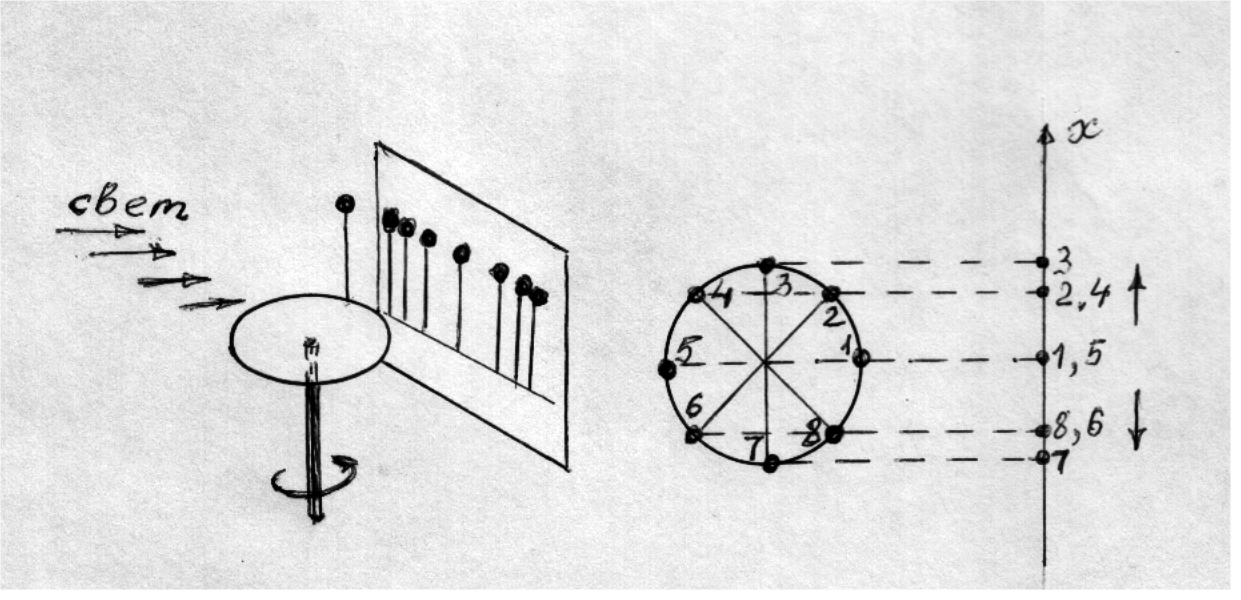
Рис.14.2. Вращательное движение материальной точки и колебательное движение её проекции на ось ох.
Механические колебания могут быть свободными и вынужденными. Если система была выведена из состояния равновесия и совершает колебания под действием сил взаимодействия между телами системы, то есть внутренних сил , то такие колебания называют свободными. Колебания груза на нити или груза на пружине являются свободными. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Простейшим видом колебаний являются гармонические колебания , которые описываются уравнением
, 14.3
Здесь
х
–смещение
тела от положения равновесия, рис 14.1.
хm
–амплитуда колебаний,
то есть максимальное смещение от
положения равновесия:
- циклическая или
круговая частота колебаний:
t- время.
Величина, стоящая под знаком косинуса
называется фазой
гармонических
колебаний. При t=0
фаза
называется
начальной фазой.
Частота
колебаний
,
циклическая частота
и период колебаний Т
связаны соотношением
14.4
При
колебательном движении тела вдоль
прямой линии (ось ох)
вектор скорости направлен всегда вдоль
этой прямой. Для гармонического закона
движения
скорость в любой момент времени находят
как производную по времени
,
то есть
, 14.5
Появление
слагаемого +
в аргументе косинуса означает изменение
начальной фазы. Максимальное по модулю
значение скорости
достигается в те моменты времени, когда
тело проходит через положение равновесия
(х=0). Аналогичным способом определяется
ускорение при гармонических колебаниях.
Ускорение а
равно производной по времени
или второй производной по времени
,
то есть
, 14.6
Знак минус в этом выражении означает, что ускорение а(t) всегда имеет знак противоположный знаку смещения x(t), и, следовательно, по второму закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия.
Графики зависимости от времени смещения, скорости и ускорения при гармонических колебаниях в случае выведения тела из положения равновесия в начальный момент времени представлены на рис.14.3.
Рис.14.3. Изменения смещения, скорости и ускорения от времени при гармонических колебаниях