1.2.Модуляция

Модуляция - изменение во времени одного или нескольких параметров сигнала в соответствии с передаваемым сообщением. Параметры сигнала, которые отображают измерения передаваемого сообщения, называют представляющими параметрами.

Дискретные сигналы, состоящие из последовательностей импульсов постоянного тока, могут быть непосредственно (без дополнительных преобразований) переданы на то или иное расстояние только по некоторым видам каналов, обеспечивающих прохождение спектра этих сигналов. Для надёжной передачи дискретных сигналов применяется модуляция.

При передаче двоичных сигналов, модулированный сигнал характеризуется двумя различными состояниями: двумя амплитудами при амплитудной модуляции, двумя частотами при частотной модуляции и двумя фазами при фазовой модуляции.

В двоичном канале передаются двоичные сигналы, условно обозначаемые цифрами “0”и “1”. Их называют двоичными единицами информации или битами.

Рекомендации МККТТ V.1 и V.24 определяют значения двоичных единиц при различных видах модуляции:

Таблица 1

Виды модуляции	“0”	“1”
Однополярная	Бестоковая посылка	Токовая посылка
Двухполярная	Положительная посылка	Отрицательная посылка
Амплитудная	Ток выключен	Ток включён
Частотная	Верхняя частота	Нижняя частота
Фазовая	Фаза, противоположная опорной фазе	Опорная фаза
Относительная фазовая	Переворот фазы	Отсутствие переворота фазы

На рисунке 1.2 приведены сигналы, соответствующие некоторым видам модуляции, передаваемой двоичной последовательности.

ν Двоичная последовательность

1 0 0 1 1 0 1 0 1

Однополярный сигнал

t

Двухполярный сигнал

t

Амплитудная модуляция

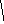
t

Импульсно-кодовая модуляция

t

Рис.1.2

Введём понятия, характеризующие процесс передачи дискретных сигналов во времени.

Значащие моменты - точки на оси времени, в которые происходят изменения дискретного сигнала ( Рис.1.3).

.

Рис.1.3

Значащие интервалы - интервалы времени между соседними значащими моментами (Рис.1.4).

Рис.1.4

Значащие позиции - фиксированные значения представляющего параметра сигнала на значащем интервале (Рис.1.5).

t₀ t₀

Рис.1.5

Минимальный по длине значащий интервал, которому кратны все значащие интервалы, называют единичным интервалом. Его обозначают специальным значком t₀. Элемент сигнала, имеющий продолжительность, равную единичному интервалу t₀, называют единичным элементом. Таким образом, t₀-длина единичного элемента во времени.