Розв’язання

З табл. 1 випливає, що кожній групі за факторною ознакою х — тривалість закордонної поїздки — відповідає певний умовний розподіл страхових полісів за результативною ознакою у — денна вартість страхових полісів. Умовні розподіли істотно відрізня­ються між собою та від безумовного, що свідчить про наявність стохастичного зв’язку. Кореляційний зв’язок можна виявити за допомогою оцінок лінії регресії — групових середніх значень результативної ознаки , обчислених за формулою середньої арифметичної зваженої для кожного інтервалу за ознакою х. Так, для першої групи полісів з тривалістю поїздки до 8 днів маємо:

=

а для сукупності в цілому

=

Розраховані в такий спосіб групові середні подано в табл. 1. Їх поступова зміна (зменшення) від групи до групи свідчить про наявність кореляційного зв’язку. Ефект впливу тривалості поїзд­ки на денну вартість страхового полісу визначається як відно­шення таких приростів: , , ; . Отже, зі збільшенням тривалості поїздки на 1 день середньоденна вартість страхового полісу скорочується в середньому на : = – – 13,3 : 7 = – 1,9 (цента) та на 1 цент.

Щоб оцінити щільність зв’язку за допомогою кореляційного відношення потрібно обчислити відповідні дисперсії. Загальна дисперсія вартості страхових полісів за даними табл. 1 становить:

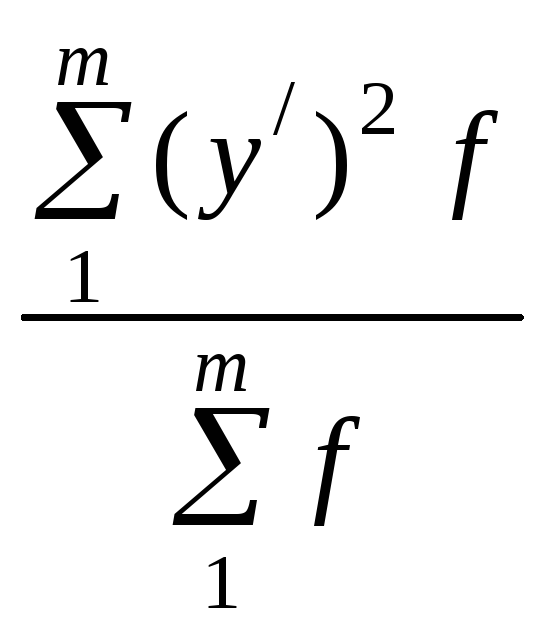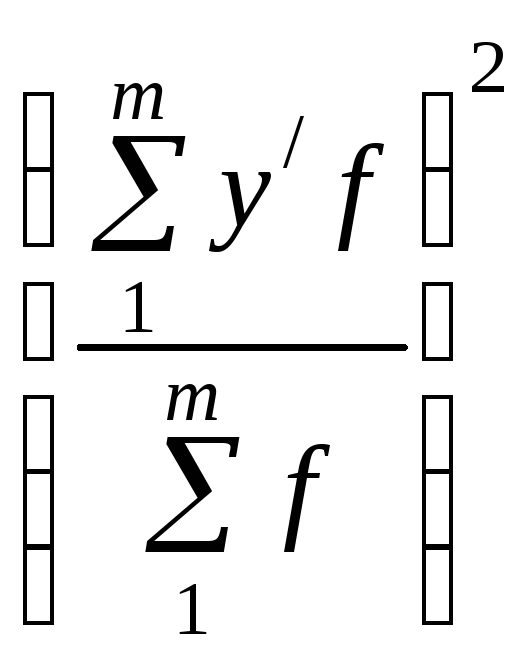= – = = 5764 – 5625 = 139.

Розрахунок міжгрупової дисперсії та аналітичне групування страхових полісів за їх денною вартістю залежно від тривалості поїздки подано в табл. 2.

Таблиця 2

Тривалість поїздки xj, днів	Кількість полісів fj	Середньоденна вартість полісу , центів
До 8	240	83,3	8,3	16533,6
8—15	160	70,0	– 5,0	4000,0
15—30	100	63,0	– 12,0	14400,0
У цілому	500	75,0	х	34933,6

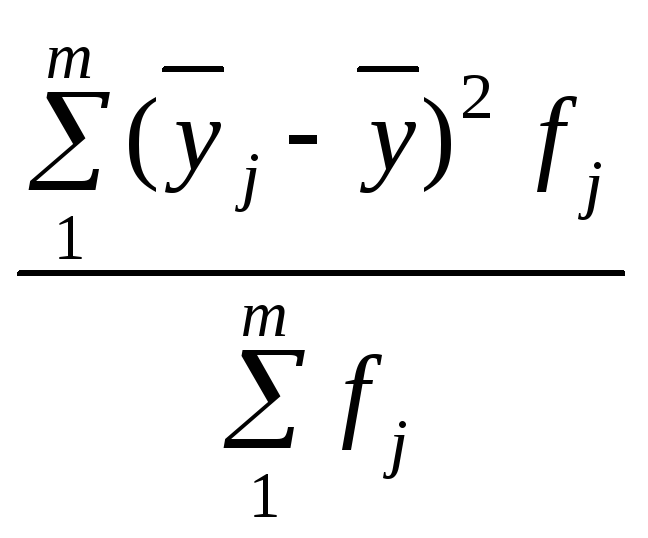= = = 69,9.

Звідси = 0,503. Отже, варіація вартості страхових полісів на 50,3 % зумовлюється варіацією тривалості поїздки та на 49,7 % — варіацією інших факторів. Тож зв’язок між ознаками досить щільний.

Щоб перевірити істотність зв’язку, беруть критичні значення (k₁, k₂). Наприклад, істотність зв’язку перевіряється з рівнем значущості  = 0,05 за таблицею критичних значень для . За табл. 2 маємо: k₁ = 3 – 1 = 2, k₂ = 500 – 3 = 497. У таблиці критичних значень останнім є k₂ = 400, тобто в сукупностях достатньо великого обсягу справджується закон великих чисел, згідно з яким у масі випадків дія випадкових причин врівно­важується, тому потреби перевіряти істотність зв’язку немає. Отже, за такого обсягу страхових полісів зв’язок визнається істотним.

Переконатися в цьому можна, порівнявши фактичне значення з його критичним значенням (2, 400) = 0,015. Оскільки = = 0,503 > 0,015, то зв’язок визнається істотним з імовірністю 0,95.

Задача 2. Обчисліть параметри лінійного рівняння регресії на прикладі зв’язку між добовою вартістю туристичних путівок в одному з туристичних агентств та тривалістю відпочинку (табл. 3).

Таблиця 3

Номер путівки	Тривалість відпочинку, днів х	Добова вар­тість путівки, грн., у	х у	х2	Y	(y – Y)2	y2
1	5	78	390	25	91,6	185,0	6084
2	14	55	770	196	52,5	6,2	3025
3	7	95	665	49	82,9	146,4	9025
4	18	30	540	324	35,1	126,0	900
5	14	53	742	196	52,5	0,2	2809
6	20	26	520	400	26,4	0,2	676
7	7	85	595	49	82,9	4,4	7225
8	15	50	750	225	48,1	3,6	2500
Разом	100	472	4972	1464	472,0	372,0	32244

Знайдемо значення величин, на підставі яких обчислюються параметри:

= 100; = 472; = 4972; = 1464; n = 8; = 100 : 8 = 12,5; = 472 : 8 = 59.

Отже, шукані параметри такі:

= – = – 4,34 (грн.);

(грн.).

Тоді рівняння регресії набирає вигляду: Y = 113,25 – 4,34 x, тобто зі збільшенням тривалості відпочинку на один день добова вартість туристичної путівки зменшується в середньому на 4,34 грн.

За даними табл. 3 обчислимо коефіцієнт еластичності:

K_ел = b = – 4,34= – 0,9.

Отже, зі збільшенням тривалості відпочинку на 1 % добова вартість путівки зменшується в середньому на 0,9 %.

На підставі рівняння регресії визначимо теоретичні значення Y. У наведеному прикладі Y — це очікувана вартість путівок за умови впливу лише тривалості відпочинку. Так, для x = 5 днів добова вартість путівки становить Y = 113,25 – = 91,6 (грн.). Це значення дещо відхиляється від емпіричного.

За даними табл. 3 обчислюємо:

залишкову дисперсію ²_e = = 372 : 8 = 46,5, загальну ²_y = = 549,5 та факторну за правилом розкладання дисперсій: ²_y = 549,5 — 46,5 = 503.

Тоді R ² = = 503 : 549,5 = 0,915, тобто маємо, що 91,5 % варіації добової вартості путівок лінійно пов’язані з варіацією тривалості відпочинку, а 8,5 % цієї варіації припадають на решту факторів. Тож зв’язок дуже щільний.

Лінійний коефіцієнт кореляції:

r =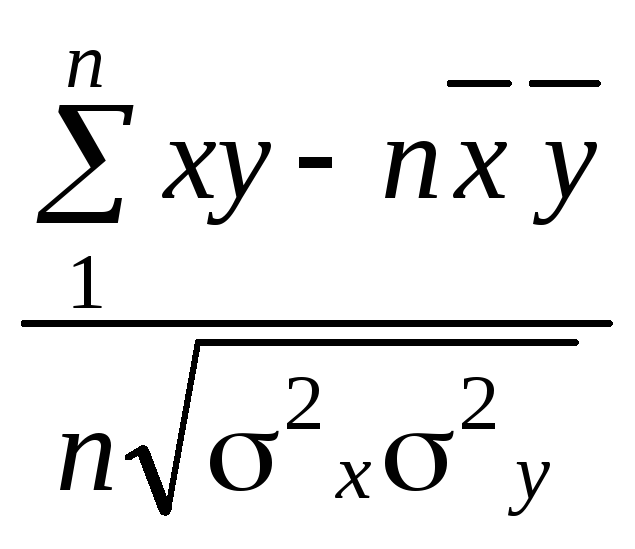== – 0,957,

де  ²_x = – 12,5² = 26,75.

Отже, зв’язок між добовою вартістю турпутівок та терміном відпочинку є щільним і оберненим.

Перевіримо істотність зв’язку. У нашому прикладі k₁ = 2 – 1 = 1, а k₂ = 8 – 2 = 6, критичне значення = 0,500 значно менше від фактичного R² = 0,915. Зв’язок між добовою вартістю путівок та тривалістю відпочинку визнається істотним з імовірністю 0,95.

Задача 3. Маємо дані маркетингового обстеження телеглядачів щодо ефективності використання рекламного часу (табл. 4).

Таблиця 4

Місце реклами в ефірному часі	Кількість респондентів, які дивляться телерекламу		Разом
	уважно	неуважно
Під час фільму	45	15	60
Перед фільмом	12	28	40
Разом	57	43	100

Зробіть відповідні висновки.

Для оцінювання ефективності використання рекламного часу за даними 4-клітинкової таблиці взаємної спряженості доречно скористатись показником відношення шансів:

w = = .

Отже, шанси зосередити увагу телеглядачів на телерекламі у 7 разів вищі в разі її показу під час фільму, ніж до нього.