
- •Введение
- •1. Цель работы
- •2. Основные понятия о векторах
- •3. Критерий равенства двух векторов
- •4. Координаты точек на прямой, плоскости и в пространстве
- •5. Две теоремы о проекции вектора на ось
- •6. Сложение векторов
- •7. Умножение вектора на скаляр
- •8. Линейно зависимые и линейно независимые векторы
- •9. Разложение вектора по координатным ортам
- •10. Критерии коллинеарности двух векторов
- •11. Деление отрезка в данном отношении
- •12. Скалярное произведение двух векторов
- •13. Понятие векторного произведения двух векторов
- •14. Смешанное произведение трёх векторов
- •15. Свойства векторного произведения двух векторов
- •16. Представление смешанного произведения трёх векторов через проекции перемножаемых векторов на коордонатные оси
- •17. Двойное векторное произведение трёх векторов
- •18.Угол между векторами
- •19. Критерий коллинеарности двух векторов
- •20. Критерии перпендикулярности двух векторов
- •21. Критерии компланарности трёх векторов
- •23. Площадь треугольника
7. Умножение вектора на скаляр
Определение.
Произведением вектора
![]() на скаляр
на скаляр
![]() называется вектор, модуль которого
равен произведению модулей сомножителей,
а направление совпадает с направлением
вектора
называется вектор, модуль которого
равен произведению модулей сомножителей,
а направление совпадает с направлением
вектора
![]() ,
если число
,
если число
![]() положительно, и противоположно направлению
вектора
положительно, и противоположно направлению
вектора
![]() ,
если число
,
если число
![]() отрицательно.
отрицательно.
Произведение
вектора
![]() на скаляр
на скаляр
![]() обозначается
обозначается
![]() или
или
![]() .
По определению:
.
По определению:
-
 ;
; -
 ,
если
,
если
 ,
, 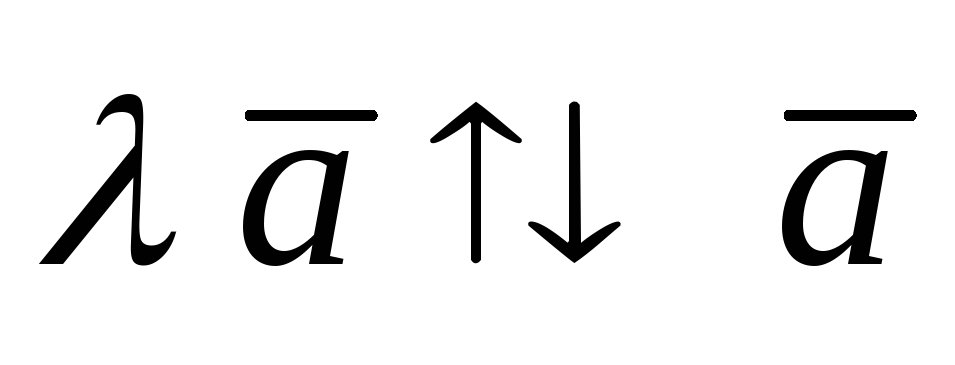 ,
если
,
если
 ;
; -
если
 ,
то
,
то
 ;
; -
если
 ,
то
,
то
 .
.
Согласно
определению, произведение вектора
![]() на скаляр
на скаляр
![]() есть вектор, коллинеарный вектору
есть вектор, коллинеарный вектору
![]() .
.
Теорема (о проекции на ось произведения вектора на скаляр). Проекция на ось произведения вектора на скаляр равна произведению этого скаляра на проекцию рассматриваемого вектора на ту же ось, т.е.
![]() ,
,
где
![]() - любая ось.
- любая ось.
Доказательство. По теореме о проекции вектора на ось
![]() ,
,
где
![]() - орт оси
- орт оси
![]() .
Если в правой части этого равенства
воспользоваться определением понятия
модуля произведения вектора на скаляр,
то получим
.
Если в правой части этого равенства
воспользоваться определением понятия
модуля произведения вектора на скаляр,
то получим
![]() (*)
(*)
При этом возможны следующие случаи:
-
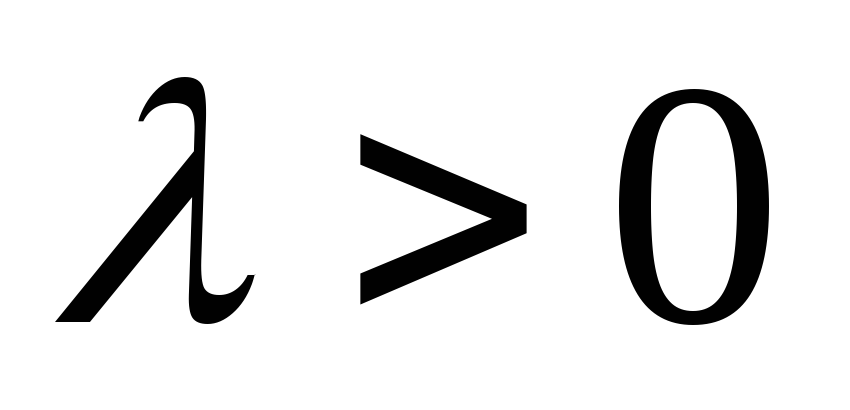 .
.
В
этом случае по определению модуля числа
![]() .
Кроме того, при
.
Кроме того, при
![]()
![]() ,
и поэтому
,
и поэтому
![]() .
Следовательно, в силу равенства (*) имеем
.
Следовательно, в силу равенства (*) имеем
![]() .
.
Если теперь в правой части последнего равенства воспользоваться свойством сочетательности умножения чисел и применить теорему о проекции вектора на ось, то получим
![]() .
.
В
этом случае по определению модуля числа
![]() .
Кроме того, при
.
Кроме того, при
![]()
![]() ,
т.е.
,
т.е.
![]() и потому
и потому
![]() .
.


Исходя из равенства (*), приходим к выводу, что в рассматриваемом случае
![]() ,
,
и
потому, как и при
![]() ,
имеем
,
имеем
![]() .
.
В
справедливости утверждения при
![]() предлагаем убедиться самостоятельно.
предлагаем убедиться самостоятельно.
Основные свойства операции умножения вектора на скаляр
1. Умножение вектора на скаляр обладает свойством сочетательности, т.е.
![]() .
.
Доказательство.
Для того, чтобы доказать, что векторы
![]() и
и
![]() равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
![]() - произвольная ось. Найдем проекции
векторов
- произвольная ось. Найдем проекции
векторов
![]() и
и
![]() на ось
на ось
![]() .
Применяя теорему о проекции на ось
произведения вектора на скаляр, имеем
соответственно
.
Применяя теорему о проекции на ось
произведения вектора на скаляр, имеем
соответственно
![]()
и
![]()
В силу свойства сочетательности умножения чисел правые части двух последних равенств совпадают, и потому
![]() ,
,
где
![]() - любая ось. Следовательно, по критерию
равенства векторов,
- любая ось. Следовательно, по критерию
равенства векторов,
![]() .
.
2. Умножение вектора на скаляр обладает свойством распределительности по отношению к сумме скаляров, т.е.
![]() .
.
Доказательство.
Для того, чтобы доказать, что векторы
![]() и
и
![]() равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
![]() -произвольная ось. Согласно теореме о
проекции на ось произведения вектора
на скаляр, имеем
-произвольная ось. Согласно теореме о
проекции на ось произведения вектора
на скаляр, имеем
![]() ,
,
или, учитывая свойство распределительности действий над числами,
![]() .
.
Если же теперь в каждом слагаемом в правой части применить теорему о проекции на ось произведения вектора на скаляр, а затем воспользоваться теоремой о проекции суммы двух векторов на ось, то придем к выводу, что
![]() ,
,
где
![]() - любая ось. Следовательно, на основании
критерия равенства векторов,
- любая ось. Следовательно, на основании
критерия равенства векторов,
![]() .
.
3. Умножение вектора на скаляр обладает свойством распределительности по отношению к сумме векторов, т.е.
![]()
Доказательство.
Для того, чтобы доказать, что векторы
![]() и
и
![]() равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
равны, достаточно доказать, что равны
их проекции на любую ось. Пусть
![]() - произвольная ось. По теореме о проекции
на ось произведения вектора на скаляр
- произвольная ось. По теореме о проекции
на ось произведения вектора на скаляр
![]() .
.
Если в правой части применить теорему о проекции суммы векторов на ось, то получим
![]() ,
,
или, в силу свойства распределительности действий над числами,
![]() .
.
Если же в каждом слагаемом правой части ещё раз воспользоваться теоремой о проекции на ось произведения вектора на скаляр, а затем теоремой о проекции суммы векторов на ось, то придем к выводу, что
![]() ,
,
где
![]() - любая ось. Следовательно, по критерию
равенства векторов,
- любая ось. Следовательно, по критерию
равенства векторов,
![]() ,
,
что и требовалось доказать.
Теорема о противоположных векторах
Произведение
вектора
![]() на
на
![]() есть вектор, противоположный вектору
есть вектор, противоположный вектору
![]() .
.
Доказательство.
Действительно,
![]() ,
,
т.е.
![]() и, кроме того,
и, кроме того,
![]()
Утверждение доказано.
Вектор
![]() обозначают
обозначают
![]() .
Введем теперь понятие разности двух
векторов.
.
Введем теперь понятие разности двух
векторов.
Определение.
Разностью векторов
![]() и
и
![]() называется вектор, равный сумме вектора
называется вектор, равный сумме вектора
![]() и вектора, противоположного вектору
и вектора, противоположного вектору
![]() .
.
Разность
векторов
![]() и
и
![]() обозначается
обозначается
![]() .По
определению
.По
определению
![]() .
.
Имеет
место равенство
![]() ,
где
,
где
![]() - любая ось.
- любая ось.
Если воспользоваться этой формулой, то нетрудно привести ещё одно доказательство, наряду с рассмотренным ранее, критерия равенства двух векторов. Рекомендуем проделать это самостоятельно.
