4. Оптимальная триангуляция многоугольника

Несмотря на свою геометрическую формулировку, эта задача очень близка к задаче о перемножении матриц.

Многоугольник (polygon)—это замкнутая кривая на плоскости, составленная из отрезков, называемых сторонами (sides) многоугольника. Точка, в которой сходятся две соседние стороны, называется вершиной (vertex). Несамопересекающийся многоугольник (только такие мы и будем, как правило, рассматривать) называется простым (simple). Множество точек плоскости, лежащих внутри простого многоугольника, называется внутренностью (interior) многоугольника, объединение его сторон называется его границей (boundary), а множество всех остальных точек плоскости называется его внешностью (exterior). Простой многоугольник называется выпуклым (convex), если для любых двух точек, лежащих внутри или на границе многоугольника, соединяющий их отрезок целиком лежит внутри или на границе многоугольника.

Выпуклый многоугольник можно задать, перечислив его вершины против часовой стрелки: многоугольник P=(v₀,v₁,...,v_n-1) имеет п сторон . Здесь v_n— то же самое, что v₀ (удобно нумеровать вершины n- угольника вычетами по модулю n).

Если v_i и v_j — две вершины, не являющиеся соседними, отрезок ; называется диагональю (chord) многоугольника. Диагональ разбивает многоугольник на два: и . Триангуляция (triangulation) многоугольника- это набор диагоналей, разрезающих многоугольник на треугольники; сторонами этих треугольников являются стороны исходного

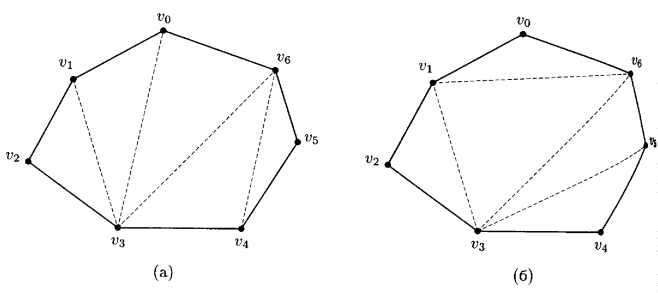
Рис. 4. Две триангуляции выпуклого семиугольника. Каждая делит семиугольник на 7-2=5 треугольников с помощью 7-3=4 диагоналей.

На рис. 4 изображены две триангуляции семиугольника. (Триангуляцию можно также определить как максимальное множество диагоналей, не пересекающих друг друга.)

Во всех триангуляциях n-угольника одно и то же число треугольников (сумма всех углов многоугольника равна произведению 180° и числа треугольников в триангуляции), а именно п-2. При этом используются n-3 диагональ (проводя диагональ, мы увеличиваем число частей на 1).

Задача об оптимальной триангуляции (optimal triangulation problem) cocтоит в следующем. Дан выпуклый многоугольник Р= (v₀,v₁,...,v_n-1) и весовая функция w, определённая на множестве треугольников с вершинами в вершинах Р. Требуется найти триангуляцию, для которой сумма весов треугольников будет наименьшей.

Естественный пример весовой функции—функция

где |v_iv_j| обозначает евклидово расстояние между v_i и v_j. Мы построим алгоритм решения этой задачи, который применим для любой весовой функции.

Триангуляции и расстановки скобок

Существует удивительная связь между триангуляциями многоугольника и расстановками скобок (скажем, в произведении последовательности матриц). Проще всего объяснить эту связь с помощью деревьев.

Полной расстановке скобок соответствует так называемое дерево разбора (parse tree) выражения. На рис. 5(а) изображено дерево разбора для

((A₁(A₂A₃))(A₄(A₅A₆))). (6)

Рис. 5. Деревья разбора. (а) Дерево разбора для ((A₁(A₂A₃))(A₄(A₅A₆))),соответствующее также триангуляции на рис. 4(а). (б) Соответствие между триангуляцией многоугольника и бинарным деревом. Матрица А_i соответствует стороне (i = 1, 2,... ,6). (в) Триангуляция и соответствующая ей расстановка скобок.

В его листьях стоят матрицы-сомножители, а в вершинах—их произведения: в каждой вершине стоит произведение двух выражений, стоящих в её детях.

Триангуляцию выпуклого многоугольника (v₀,v₁,...,v_n-1) также можно изобразить в виде дерева. Листьями его будут стороны многоугольника (кроме ) Остальные вершины—это диагонали триангуляции плюс сторона ;эту последнюю объявим корнем.

Построение дерева (на примере триангуляции рис. 4(а)) показано на рис. 5(6). Для начала мы смотрим, в какой треугольник попал корень . В нашем случае это . Детьми корня будем считать две другие стороны этого треугольника. Триангуляция состоит из этого треугольника и двух триангуляций оставшихся частей ((v₀,v₁,v₂,v₃) и (v₃,v₄,v₅,v₆), рис. 5(6)), причём диагонали, являющиеся детьми корня, являются сторонами этих многоугольников ( и на рис. 5(6)). Повторим для каждой из них ту же конструкцию: рассмотрим треугольник триангуляции нового многоугольника, содержащий выделенную сторону, две другие стороны этого треугольника объявим её детьми и т. д. В конце концов мы придём к бинарному дереву с п-1 листом. Действуя в обратном порядке, можно по бинарному дереву построить триангуляцию. Построенное соответствие между триангуляциями и бинарными деревьями является взаимно однозначным.

Вспоминая, что полные расстановки скобок в произведении п сомножителей находятся во взаимно однозначном соответствии с бинарными деревьями с листьями, получаем взаимно однозначное соответствие между полными расстановками скобок в произведении п матриц и триангуляциями (п+1)-угольника. При этом матрица A в произведении A₁A₂...A_n соответствует стороне , а диагональ (1≤i<j≤n) соответствует произведению A_i..j.

Это соответствие можно понять и без деревьев. Напишем на всех сторонах триангулированного многоугольника, кроме одной, по сомножителю. Далее поступаем так: если в треугольнике две стороны уже помечены, то на третьей мы пишем их произведение. На первоначально непомеченной стороне появится полная расстановка скобок (см. пример на рис. 5(в)).

Заметим, что задача о перемножении матриц является частным случаем задачи об оптимальной триангуляции. Пусть нам нужно вычислить A₁...A_n,, где A_i является p_i-1* р_i- матрицей. Рассмотрим (n+1)-угольник Р=(v₀,v₁,...,v_n) и весовую функцию

Тогда стоимость триангуляции будет равна числу умножений при соответствующей расстановке скобок.

Хотя задача о перемножении матриц является лишь частным случаем задачи об оптимальной триангуляции, оказывается, что алгоритм matrix-chain-order из раздела 1 легко приспособить для решения задачи о триангуляции. Надо только в его заголовке заменить р на v и строку 10 заменить на такую:

q = m[i][ k] + m[k + 1][j] + p[i]p[j]p[k]

В результате работы алгоритма m[1,n] станет равным весу оптимальной триангуляции.

Рекуррентная формула

Другими словами, имеет место следующая рекуррентная формула. Пусть m[i,j] —вес оптимальной триангуляции многоугольника (v_i-1v_i,...,v_j),где 1≤i<j≤n. Вес оптимальной триангуляции всего многоугольника равен m[1,n]. Будем считать, что «двуугольники» (v_i-1v_i) имеют вес 0. Тогда m[i,i] = 0 для i=1, 2,...,п. Если j-i≥ 1, то у многоугольника (v_i-1v_i,...,v_j) имеется не менее трёх вершин, и нам необходимо найти минимум (по всем k из промежутка i≤k≤j-1) такой суммы: вес плюс вес оптимальной триангуляции (v_i-1v_i,...,v_k) плюс вес оптимальной триангуляции (v_k,v_k+1,...,v_j). Поэтому

Единственное отличие этой формулы от формулы (2)—более общий вид весовой функции. Стало быть, алгоритм matrix-chain-order с указанными выше изменениями вычисляет вес оптимальной триангуляции; время работы 0(n³), объём используемой памяти 0(n²).

Замечания

Систематическое изучение динамического программирования было начато Р.Беллманом в 1955 году [21], хотя некоторые приёмы такого рода были известны и ранее. Кстати, слово «программирование» (programming) в словосочетаниях «динамическое программирование» (dynamic programming), а также «линейное программирование» (linear programming) не означает составление программ для компьютера.

Ху и Шинг [106] придумали работающий за время 0(n log n) алгоритм для задачи о порядке перемножения матриц; они же указали соответствие между этой задачей и задачей об оптимальной триангуляции.

Алгоритм для нахождения наибольшей общей подпоследовательности за время 0(тп) относится, видимо, к фольклору. В работе [43] Кнут поставил вопрос, возможен ли для этой задачи субквадратичный алгоритм. Масек и Патерсон [143] показали, что возможен, найдя алгоритм, работающий за время 0(mn / logn) при п ≤ т и фиксированном размере множества, из которого берутся члены последовательностей. Для случая, когда в последовательностях нет повторений, алгоритм с оценкой 0((п + т) log(n + т)) построен в статье Шимански [184]. Многие из этих результатов обобщаются на задачу о стоимости редактирования.

ЗАКЛЮЧЕНИЕ

В результате проделанной работы была изложена теория динамического программирования в пояснительной записке. По тексту размещены алгоритмы процедур, переведённых с языка Pascal в язык программирования Си, который является предметом изучения данного курса. Приведённые алгоритмы иллюстрируют методику динамического программирования и возможности составления оптимальных алгоритмов, которые дают возможность экономить память и время выполнения программ.