Построение бинарного дерева
Бинарное дерево состоит из коллекции объектов TreeNode, связанных посредством своих полей с указателями. Объект TreeNode создается динамически с помощью функции new.
TreeNode<int>
*p;
// о!5ъявление указателя
// на целочисленный
узел дерева
р - new
TreeNode(item);
// левый и правый указатели равны NULL
// создать объект TreeNode с указательными полями Iptr и rptr.
//по умолчанию указатели содержат NULL.
template <class T>
TreeNode<T> *GetTreeNode(T item, TreeNode<T> *lptr - NULL,
TreeNode<T> *rptr - NULL) { TreeNode<T> *p;
// вызвать new для создания нового узла // передать туда параметры Iptr и rptr р =new TreeNode<T> (item, Iptr, rptr);
// если памяти недостаточно, завершить программу сообщением об ошибке
if (p == HULL)
cerr « "Ошибка при выделении памяти!\п"; exit(l);
// вернуть указатель на выделенную системой память return p; }
Функция FreeTreeNode принимает указатель на объект TreeNode и освобождает занимаемую узлом память, вызывая функцию C++ delete.
// освободить динамическую память, занимаемую данным узлом
template <class t>
void FreeTreeNode(TreeNode<T> *p)
{
delete p; ) . -
Обе эти функции находятся в файле treelib.h вместе с функциями обработки бинарного дерева, представленными в разделе 11.2.
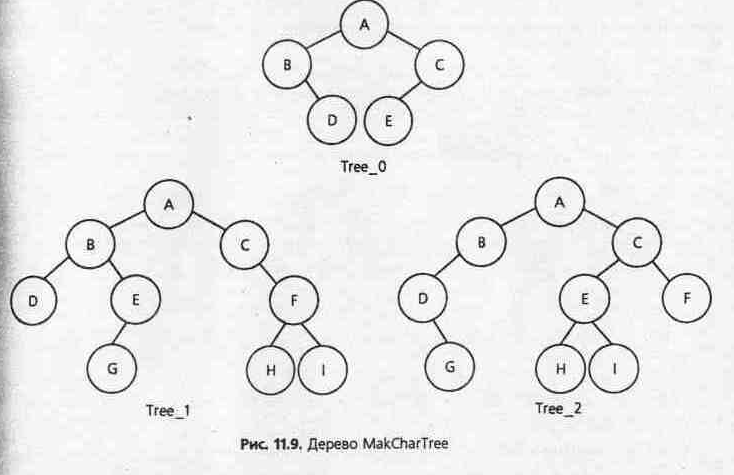
Пример определения дерева. Функция GetTreeNode может быть использована для явного построения каждого узла дерева и, следовательно, всего дерева. Это было продемонстрировано на дереве с тремя узлами, содержащими 10, 20 и 30. Для более крупного экземпляра процесс будет немного утомительным, так как вы должны включить в дерево все значения данных я указателей.В этой главе создадим функцию MakeCharTree, строящую три дерева, узлы которых содержат символьные элементы данных. Эти деревья будут использоваться для иллюстрации методов TreeNode в следующем разделе. Параметры функции включают в себя ссылку на корень дерева и число n (О < n < 2), которое служит для обозначения дерева. Следующие объявления создают указатель на объект TreeNode, с именем root, и назначают его корнем дерева Тгее_2.
jreeNode<char> *root; // объявить указатель на корень MakeCharTree(root,2); // сформировать на этом корне дерево tree_2
На рис. 11.9 показаны три дерева, построенных этим методом. Полный листинг функции MakeCharTree находится в файле treelib.h. Эта функция распространяет технологию из примера 11.2 на деревья с пятью и девятью
11.2. Разработка функций класса TreeNode
Связанный список – это линейная структура, позволяющая последовательно проходить узлы, используя указатель на следующий элемент. Поскольку дерево является нелинейной структурой, похожего алгоритма прохождения не существует. Мы вынуждены выбрать один из методов прохождения, среди которых наиболее широко используются прямой, симметричный в обратный методы. Каждый из них основывается на рекурсивной структуре бинарного дерева.
Алгоритмы прохождения существенно влияют на эффективность использования дерева. В первую очередь мы разработаем методы рекурсивного про-
хождения, а затем на их основе создадим алгоритмы печати, копирования и удаления, а также определения глубины дерева. Мы также рассмотрим поперечный метод (breadth first) прохождения, который использует очередь для запоминания узлов. Этот метод сканирует дерево уровень за уровнем, начиная с корня и передвигаясь к первому поколению сыновей, затем ко второму и т.д. Метод находит важное применение в административных иерархиях, где власть распределяется от главы к другим уровням управления. Наша реализация метода прохождения предусматривает параметр-функцию visit, которая осуществляет доступ к содержащимся в узле данным, Передавая в качестве параметра функцию, можно указать некоторое действие, которое должно выполняться в каждом узле в процессе прохождения дерева.
template <class T>
void <Метод_прохода> (TreeNode<T> *t, void visit(TS item));
Всякий раз при вызове метода клиент должен передавать имя функция, выполняющей некоторое действие с данными, имеющимися в узле. По мере того как метод перемещается от узла к узлу, вызывается эта функция и выполняется предусмотренное действие.
Замечание. Понятие параметра-функции является относительно простым, но требует некоторого пояснения. В общем случае функция может быть аргументом, если указать ее имя, список параметров и возвращаемое ею значение. Пусть, например, функция G имеет параметр-функцию f. В этом параметре указывается имя функции (f), список параметров (int x) и возвращаемый тип (int).
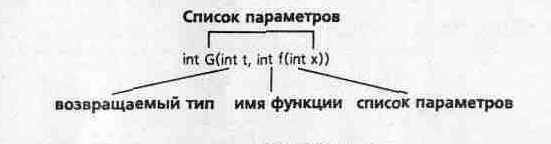
int G(int t, int flint x)) // параметр-функция f {
// вычислить f(t) с помощью функции f и параметра t.
// возвратить произведение этого значения и t
return t * f(t); }
Вызывая функцию G, клиент должен передать функцию для f с той же структурой. Пусть в нашем примере клиент определил функцию XSquared, вычисляющую х2.
// XSquared – целочисленная функция с целочисленным параметром х
int XSquared(int x)
{
return х*х; )
Клиент вызывает функцию G с целочисленным параметром t и параметром-функцией XSquared. Оператор
Y = G(3, XSquared)
вызывает функцию G, которая в свою очередь вызывает функцию XSquared с параметром 3. Оператор cout печатает результат 27.
cout « G(3.0, XSquared) « endl;
Рекурсивные методы прохождения деревьев
Рекурсивное определение бинарного дерева определяет эту структуру как корень с двумя поддеревьями, которые идентифицируются полями левого и правого указателей в корневом узле. Сила рекурсии проявляется вместе с методами прохождения. Каждый алгоритм прохождения дерева выполняет в узле три действия: заходит в узел, рекурсивно спускается по левому поддереву и по правому поддереву. Спустившись к поддереву, алгоритм определяет, что он находится в узле, и может выполнить те же три действия. Спуск прекращается по достижении пустого дерева (указатель == NULL). Различные алгоритмы рекурсивного прохождения отличаются порядком, в котором они выполняют свои действия в узле. Мы изложим симметричный и обратный методы, в которых сначала осуществляется спуск по левому поддереву, а затем по правому. Другие методы оставляем вам в качестве упражнений.
Симметричный метод прохождения дерева
Симметричный метод прохождения начинает свои действия в узле спуском по его левому поддереву. Затем выполняется второе действие – обработка данных в узле. Третье действие – рекурсивное прохождение правого поддерева. В процессе рекурсивного спуска действия алгоритма повторяются в каждом новом узле.
Итак, порядок операций при симметричном методе следующий:
1.Прохождение левого поддерева.
2. Посещение узла. к
3. Прохождение правого поддерева.
Мы называем такое прохождение LNR (left, node, right). Для дерева Тгее_0• функции MakeCharTree "посещение" означает печать значения из поля данных узла.
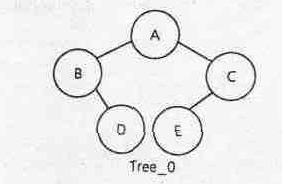
При симметричном методе прохождения дерева Тгее_0 выполняются следующие операции.
Действие Печать Замечания
Спуститься от А к В: Левый сын узла В равен NULL
Посетить В; В
Спуститься от В к D: D – листовой узел
Посетить D; D Конец левого поддерева узла А
Посетить корень А: А
Спуститься от А к С:
Спуститься от С к Е: Е – листовой узел
Посетить Е; Е
Посетить С; С Готово!
Узлы посещаются в порядке В D А Е С. Рекурсивная функция сначала спускается по левому дереву [t–>Left()]а затем посещает узел. Второй шаг рекурсии спускается по правому дереву [t–>Right()].
// симметричное рекурсивное прохождение узлов дерева template <class T>
void Inorder (TreeNode<T> *t, void visit(TS item)) {
// рекурсивное прохождение завершается на пустом поддереве if (t !- NOLL) {
Inorder(t->Left (), visit); // спуститься по левому поддереву visit(t->data); // посетить узел
Inorder(t->RightО, visit); // спуститься по правому поддереву ) )
Обратный метод прохождения дерева. При обратном прохождении посещение узла откладывается до тех пор, пока не будут рекурсивно пройдены оба его поддерева. Порядок операций дает так называемое LRN (left, right, node) сканирование.
1. Прохождение левого поддерева.
2. Прохождение правого поддерева.
3. Посещение узла.
При обратном прохождении дерева Тгее_0 узлы посещаются в порядке D В Е С А.
Действие Печать Замечания
Спуститься от А к В: Левый сын узла В равен NULL
Спуститься от В к D: D – листовой узел
Посетить D; D Все сыновья узла В пройдены
Посетить В; В Левое поддерево узла А пройдеао - Спуститься от А к С:
Спуститься от С к Е: Е – листовой узел
Посетить Е; Е Левый сын узла С
Посетить С; С Правый сын узла А
Посетить корень А: А Готово!
Функция сканирует дерево снизу вверх. Мы спускаемся вниз по левому дереву [t->Left()], а затем вниз по правому [t->Right(>]. Последней операцией является посещение узла. ;
// обратное рекурсивное прохождение узлов дерева
template <class T>
void Postorder (TreeNode<T> *t, void visit (TS item))
// рекурсивное прохождение завершается на пустом поддереве if (t !- NOLL)
{ .
Postorder(t->Left(), visit); // спуститься по левому поддереву
1Postorder(t->Right(), visit); /спуститься по правому поддереву
visit(t->data); // посетить узел
}
Прямой метод прохождения определяется посещением узла в первую очередь и последующим прохождением сначала левого, а потом правого его поддеревьев (NLR).
Ясно, что префиксы pre, in и post в названиях функций показывают, когда происходит посещение узла. В каждом случае сначала осуществлялось прохождение по левому поддереву, а уже потом по правому. Фактически существуют еще три алгоритма, которые выбирают сначала правое поддерево я потом левое. Для печати дерева будем использовать RNL-прохождение. Алгоритмы прохождения посещают каждый узел дерева. Они дают эквивалент последовательного сканирования массива или связанного списка. Функции прямого, симметричного и обратного методов прохождения содержатся в файле treescan.h.
Пример 11.2
.
1. Для символьного дерева Тгее_2 имеет место следующий порядок
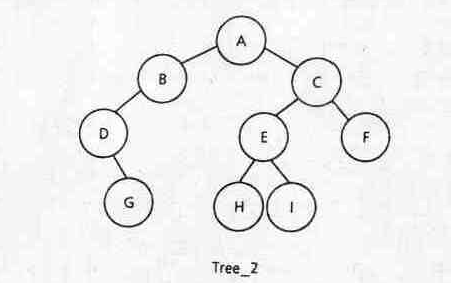
посещения узлов.
Прямой: ABDGCEHI F Симметричный: DGBAHEI C F
Обратный: GDBHI EFCA
2. Результат симметричного прохождения дерева Тгее_2 производится следующими операторами:
// функция visit распечатывает поле данных
void PrintChar(chars elem)
(
cout «elem « " "; }
TreeNode<char> "root;
MakeCharTree(root, 2); // сформировать дерево Тгее_2 с корнем root
// распечатать заголовок и осуществить прохождение, используя
// функцию PrintChar для обработки узла
cout < "Симметричное прохождение: ";
Inorder (root, PrintChar);