Бинарные деревья. Прохождение их в прямом, обратном и симметричном направлении Бинарные деревья
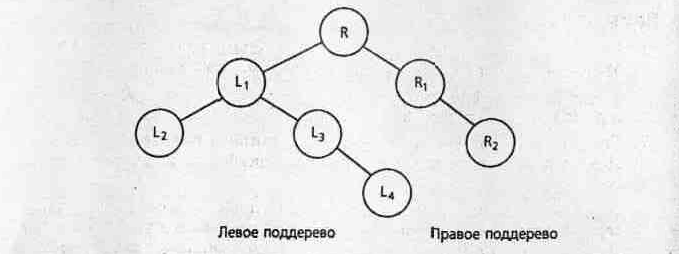
Хотя деревья общего вида достаточно важны, мы сосредоточимся на ог- раниченном классе деревьев, где каждый родитель имеет не более двух сыновей (рис. 11.6). Такие бинарные деревья (binary trees) имеют унифицированную структуру, допускающую разнообразные алгоритмы прохождения и эффективный доступ к элементам. Изучение бинарных деревьев дает возможность решать наиболее общие задачи, связанные с деревьями, поскольку любое дерево общего вида можно представить эквивалентным ему бинарным деревом. Этот вопрос рассматривается в упражнениях.
У каждого узла бинарного дерева может быть О, 1 или 2 сына. По отно-шению к узлу слева будем употреблять термин левый сын (left child), а по отношению к узлу справа – правый сын (right child). Наименования "левый" и "правый" относятся к графическому представлению дерева. Бинарное дерево является рекурсивной структурой. Каждый узел – это корень своего собственного поддерева. У него есть сыновья, которые сами являются корнями деревьев, называемых левым и правым поддеревьями соответственно. Таким образом, процедуры обработки деревьев естественно рекурсивны. Вот рекур-сивное определение бинарного дерева:
Бинарное дерево – это такое множество узлов В, что
а) В является деревом, если множество узлов пусто (пустое дерево – тоже
дерево);
6) В разбивается на три непересекающихся подмножества:
{R} корневой узел
{Li, L2, ...," Lm} левое поддерево R
{Ri, R2, ..., Rm} правое поддерево R
На любом уровне n бинарное дерево может содержать от 1 до 2n узлов. Число узлов, приходящееся на уровень, является показателем плотности дерева. Интуитивно плотность есть мера величины дерева (число узлов) по отношению к глубине дерева. На рис. 11.6 дерево А содержит 8 узлов при глубине 3, в то время как дерево В содержит 5 узлов при глубине 4. Последний случай является особой формой, называемой вырожденным (degenerate) деревом, у которого есть единственный лист (Е) и каждый нелистовой узел имеет только одного сына. Вырожденное дерево эквивалентно связанному списку.
Деревья с большой плотностью очень важны в качестве структур данных, Так как они содержат пропорционально больше элементов вблизи корня, т.е. с более короткими путями от корня. Плотное дерево позволяет хранить больше коллекции данных и осуществлять эффективный доступ к элементам.
Быстрый поиск – главное, что обусловливает использование деревьев для хранения данных.
Вырожденные деревья являются крайней мерой плотности. Другая крайность – законченные бинарные деревья (соmplete binary tree) глубины N. где каждый уровень О...К-1 имеет полный набор узлов и все листья уровня N расположены слева. Законченное бинарное дерево, содержащее 2N узлов на уровне N является полным (full). На рис, 11.7 показаны законченное и полное бинарные деревья.
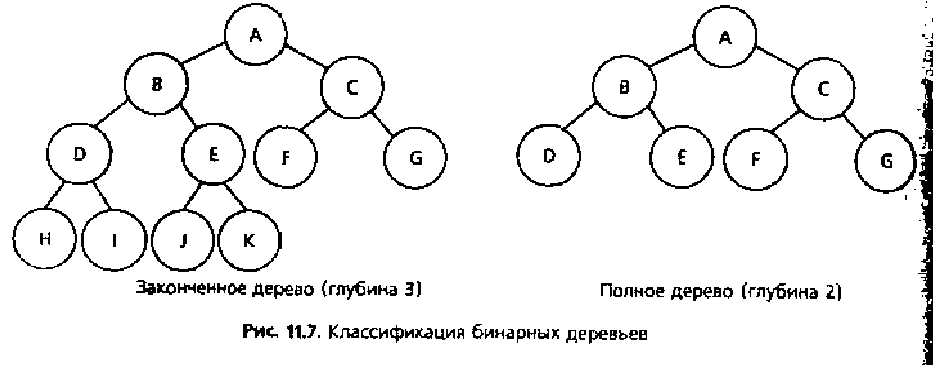
Законченные и полные бинарные деревья дают интересные математические : факты. На нулевом уровне имеется 2<> узлов, на первом – 21, на втором – 22 и т.д. На первых k-1 уровнях имеется 2k-1 узлов.
1 + 2 + 4 + ... + 2k-1 = 2k-1
На K-oуровне количество дополнительных узлов колеблется от 1 до (полное). В полном дереве число узлов равно
1 + 2 + 4 + ... + 2k-1+2k = 2k+1 -1
Число узлов законченного бинарного дерева удовлетворяет неравенству
2k< N < 2k+1 –1<2k+1
Решая его относительно K, имеем
k< 1оg (N)< k+1
Например, полное дерево глубины 3 имеет
24 – 1 = 15 узлов
Пример 11.1
1. Максимальная глубина дерева с 5-ю узлами равна 4 [рис. 11.6 (В)]. Минимальная глубина 1с дерева с 5-ю узлами равна
K<=1оg2(5) < k+1
Log2(5)=2,32 и k=2
2. Глубина дерева есть длина самого длинного пути от корня к узлу. Для вырожденного дерева с N узлами наибольший путь имеет длину N-1.
Для законченного дерева с N узлами глубина равна целой части от 1оg2N.Этому же значению равен максимальный путь. Пусть дерево имеет N = 10000 элементов, тогда максимальный путь равен
Int(log210000)=int(13,28)=13