6. Дифференциальное исчисление функций одной переменной

6.1. Дифференцирование функций

Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда при-ращение аргумента стремится к нулю:

где

Производная обозначается у', y'(x), y'_x, .

Правила дифференцирования функций. Пусть С – постоянная, а u(x) и v(x) – дифференцируемые функции. Тогда

1. C' = 0,

2. ,

3. ,

4. ,

5. .

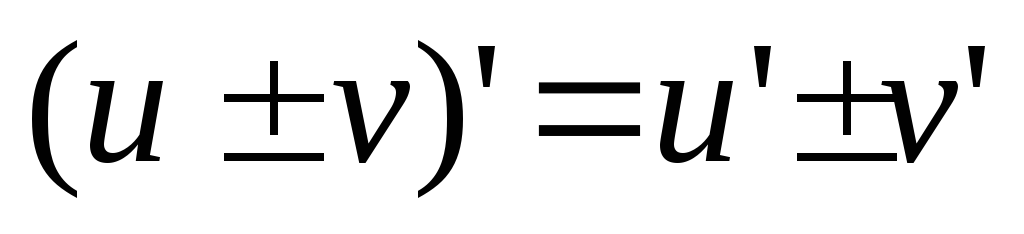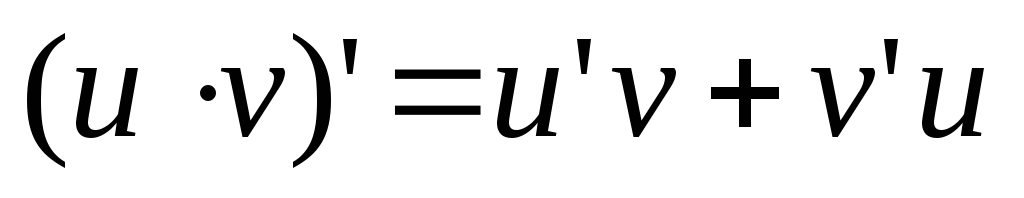Производная сложной функции y = f(u(x)). Если функция u = u(x) дифференцируема в точке х, а функция y = f(u) дифференцируема в соответствующей точке u = u(x), то сложная функция y = f(u(x)) дифференцируема в точке х и ее производная равна

Таблица производных.

1.

2.

3.

4.

5.

6.

7.

8. (

9.

10.

11.

12.

13.

14.

Функция неявно задана уравнением если для всех выполняется равенство

Для вычисления производной функции, заданной неявно, следует тождество продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x).

Пример 6.1. Найти производную показательно-степенной функции

.

Решение. Логарифмируя, а затем дифференцируя левую и правую части равенства, получим

.

Умножая обе части равенства на у, имеем:

Пример 6.2. Найти производную функции , заданной неявно уравнением .

Решение. Дифференцируя по х тождество , получим . Выражая из этого равенства, находим:

.

Дифференциал функции равен произведению ее про-изводной на приращение независимой переменной: или .

При достаточно малых имеет место приближенная формула , т.е. или .

Пример 6.3. Найти приближенное значение объема шара, радиус которого равен 1,02 м.

Решение. Воспользуемся формулой . Тогда . Полагая , получим м³.

6.2. Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически

Производной второго порядка функции называется производная от ее производной, т.е. . Аналогично определяются производные более высоких порядков .

Дифференциалы высших порядков функции (x – независимая переменная) вычисляются по формулам

.

Если функция задана параметрически соотношениями , причем , то ее первая и вторая производные находятся по формулам:

.

Пример 6.4. Найти выражение для производной n-го порядка функции .

Решение.

.

Пример 6.5. Найти производную 2-го порядка от функции , заданной неявно уравнением .

Решение. По правилу дифференцирования функции, заданной неявно, получаем:

.

Отсюда, используя равенство , имеем:

или .

Следовательно, .

Дифференцируя последнее равенство и используя найденное для выражение, получим:

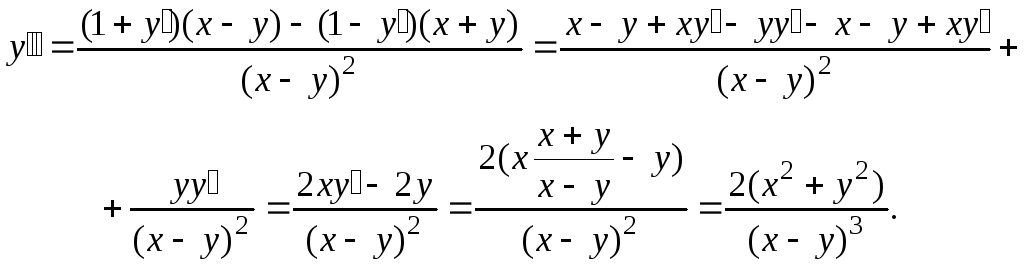
Пример 6.6. Найти производную 2-го порядка функции, заданной параметрически:

Решение.

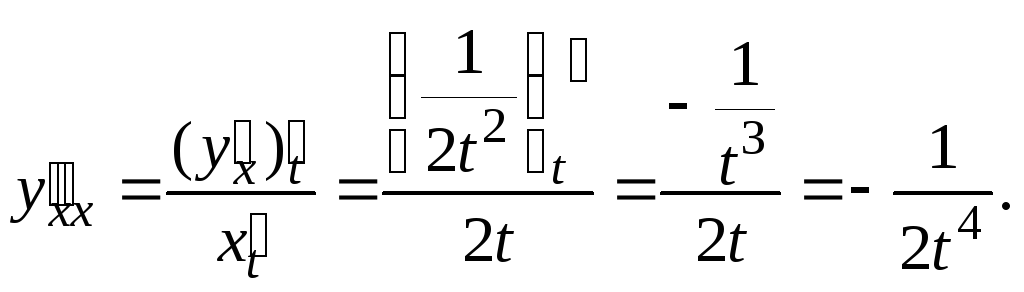
Пример 6.7. Найти дифференциалы 1-го, 2-го, …, n-го порядков функции .

Решение.