- •Эксперимент Физическая модель Прогноз Эксперимент
- •Кинематика вращательного движения
- •Динамика Динамика поступательного движения
- •Законы Ньютона
- •Т ретий закон Ньютона
- •Движение тела переменной массы
- •Система материальных точек
- •Уравнение движения системы материальных точек
- •Система материальных точек
- •Динамика Вращательного движения
- •Главные и свободные оси вращения
- •Симметрия
- •Гироскопы
- •Гироскоп на кардановом подвесе.
Движение тела переменной массы
Масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива.
В какой-то момент времени t тело имело скорость v, а массу m
За промежуток времени dt масса изменилась на m-dm, а скорость v+dv
И зменение
импульса
зменение
импульса
Ч![]() астные
случаи
астные
случаи
-
u=0 масса присоединяется (отделяется) без скорости относительно тела
![]()
-
u
 =v
присоединенная и отделенная масса
неподвижна в выбранной системе отсчета
=v
присоединенная и отделенная масса
неподвижна в выбранной системе отсчета
Рассмотрим движение ракеты в отсутствии внешних сил и при постоянной скорости выбрасываемых газов
-
Ракета движется прямолинейно
-
В
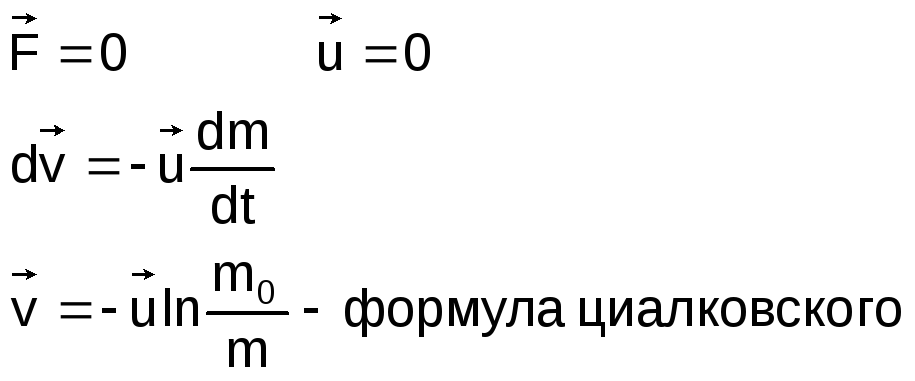 ыброс
газов происходит одновременно (m-m0)
ыброс
газов происходит одновременно (m-m0)
Начальная скорость равна нулю
П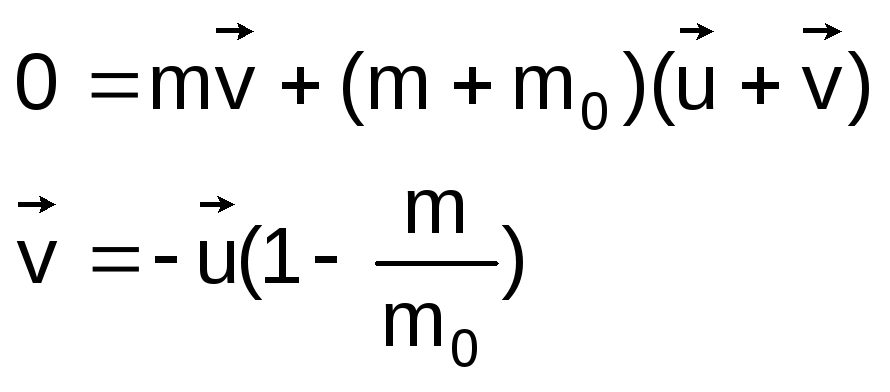 ри
непрерывном отделении массы скорость
растет неограниченно
ри
непрерывном отделении массы скорость
растет неограниченно
Система материальных точек
Механическая система- это совокупность точек конечного числа, выделенная для рассмотрения
Внутренние силы - это силы, с которыми точки системы действуют друг на друга
Внешние силы- это силы, источники которых лежат вне системы
В НИСО к внешним силам относят силы инерции
Замкнутая или изолированная система это система, в которой отсутствуют внешние силы или воздействием посторонних сил можно пренебречь.
Уравнение движения системы материальных точек
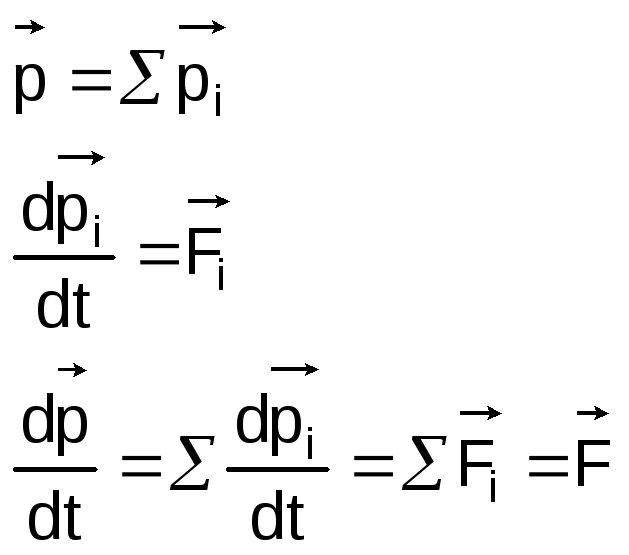
М![]() атематически
это уравнение подобно уравнению движения
материально точки. А физически эти
уравнения различны так как носители
импульса и точки приложения внешних
сил распределены по всему пространству
атематически
это уравнение подобно уравнению движения
материально точки. А физически эти
уравнения различны так как носители
импульса и точки приложения внешних
сил распределены по всему пространству
В нерелятивистском случае эти уравнения равны
И зменение
импульса системы имеет причиной действие
внешних сил
зменение
импульса системы имеет причиной действие
внешних сил
Закон сохранения импульса
Суммарный импульс материальных точек остается постоянным то есть не изменяется во времени
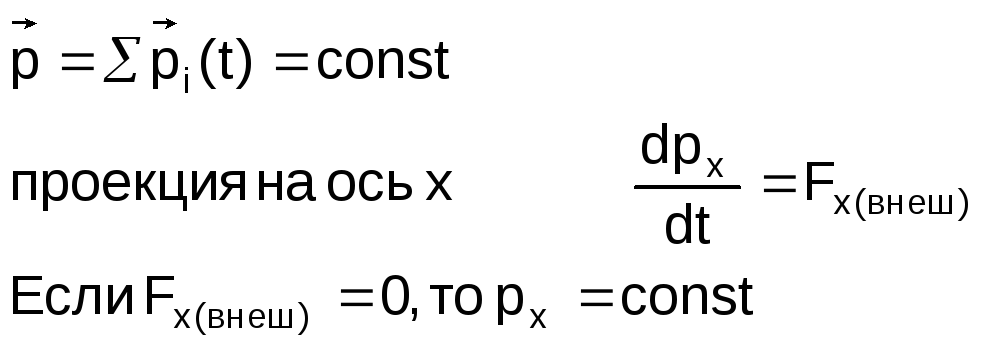 Закон
выполняется, например движение в
горизонтальном положении в однородном
поле сил тяжести.
Закон
выполняется, например движение в
горизонтальном положении в однородном
поле сил тяжести.
Закон сохранения импульса основан на свойстве пространства однородность(все законы и свойства одинаковы во всех его точках)
Система материальных точек
Рассмотрим нерелятивистский случай, то есть масса не зависит от скорости
В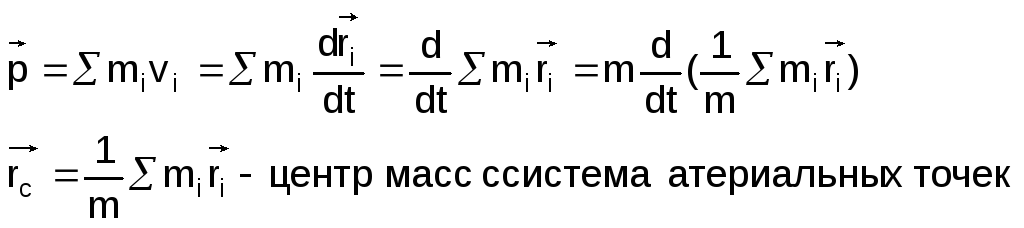 однородном поле силы тяжести центр
масс
совпадает с центром тяжести
однородном поле силы тяжести центр
масс
совпадает с центром тяжести
Е сли
центр масс системы движется прямолинейно
и равномерно, то её импульс остается
постоянным
сли
центр масс системы движется прямолинейно
и равномерно, то её импульс остается
постоянным
Центр масс замкнутой системы остается неподвижным или движется прямолинейно и равномерно, если равнодействующих внешних сил равняется нулю.
Система Отсчета, относительно которой центр масс покоится – это система центра масс.
Ц-система жестко связана с центром масс и движется поступательно относительно инерциальных систем отсчета
Динамика Вращательного движения
О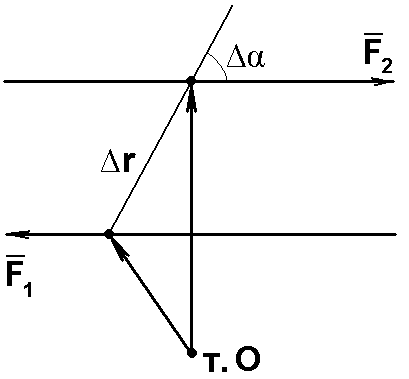 сновные
динамические параметры вращательного
движения материальной точки
сновные
динамические параметры вращательного
движения материальной точки
1 .Момент
импульса
относительно точки о. Это вектор, который
равен векторному произведению радиуса
вектора на импульс данной точки.
.Момент
импульса
относительно точки о. Это вектор, который
равен векторному произведению радиуса
вектора на импульс данной точки.
Момент импульса еще называют количество движения.
2 .Момент
силы
.Момент
силы
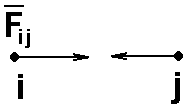
Пара сил
Пара сил – это две равные по модулю, противоположные по направлению и действующие вдоль одной прямой силы
Плечо пары - это расстояние между прямыми, вдоль которых действуют силы
М![]() омент
пары относительно любой точки одинаков
омент
пары относительно любой точки одинаков
Рассмотри изменение вектора L во времени
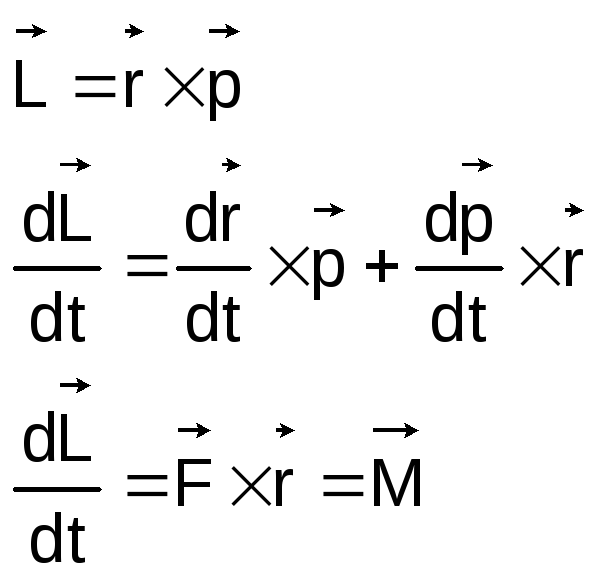
 Приращение
момента импульса частицы за какое-либо
время равняется импульсу момента силы
Приращение
момента импульса частицы за какое-либо
время равняется импульсу момента силы
![]()
Точка о принадлежит оси Z

Р ассмотрим
систему материальных точек
ассмотрим
систему материальных точек
Сумма всех внутренних сил равна нулю это силы гравитационного и кулоновского взаимодействия между двумя частицами образуют пару с плечом равным нулю
Момент импульса твердого тела относительно оси вращения равняется :
m![]() iri
-
масса и расстояние от оси вращения до
i-ой
частицы
iri
-
масса и расстояние от оси вращения до
i-ой
частицы
![]()
Момент инерции зависит от распределения массы относительно оси и является аддитивной величиной.
|
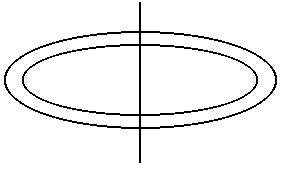
Обруч (кольцо) |
|
|
|
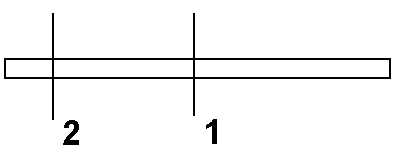
Тонкий стержень |
|
1. 2.
|
|
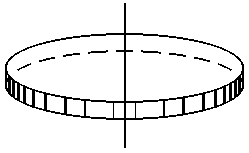
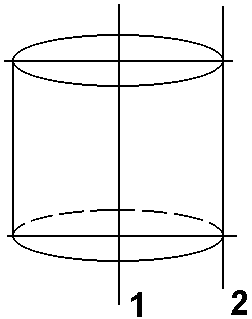
Диск (цилиндр) |
1. 2.
|
|
|
Шар (сферическая оболочка) |
|
|
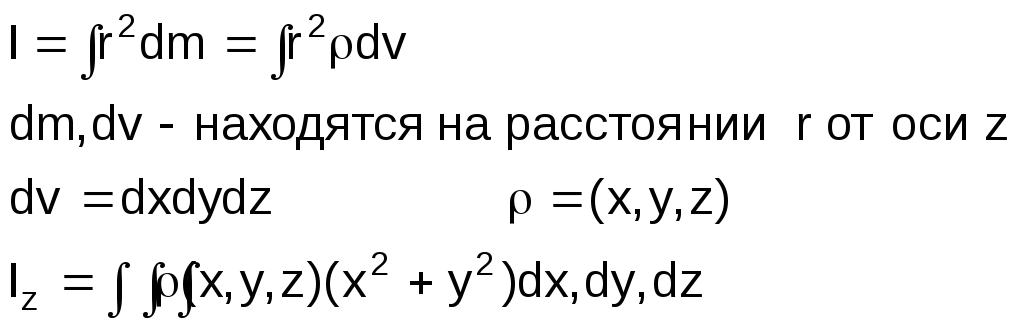
![]() Теорема
Штейнера: Момент инерции относительно
произвольной оси
равен сумме момента инерции относительно
оси параллельной данной, и проходящей
через центр масс тела и произведение
массы тела на квадрат расстояния между
осями
Теорема
Штейнера: Момент инерции относительно
произвольной оси
равен сумме момента инерции относительно
оси параллельной данной, и проходящей
через центр масс тела и произведение
массы тела на квадрат расстояния между
осями
Уравнение динамики вращения твердого тела
![]()
Интегрируем по времени
Для абсолютно твердого тела момент инерции не зависит от времени
П роведем
аналогию
величин вращательного и поступательного
движения
роведем
аналогию
величин вращательного и поступательного
движения
|
Поступательное |
Вращательное |
|
Линейное перемещение S=V0t
|
Угловое перемещение =0
|
|
Линейная скорость V=V0 a t |
Угловая скорость =0 t |
|
Масса m |
Момент инерции I |
|
F=ma |
M=I |
|
F=( |
M= |
З![]()
![]() акон
сохранения момента импульса
акон
сохранения момента импульса
Рассмотрим систему
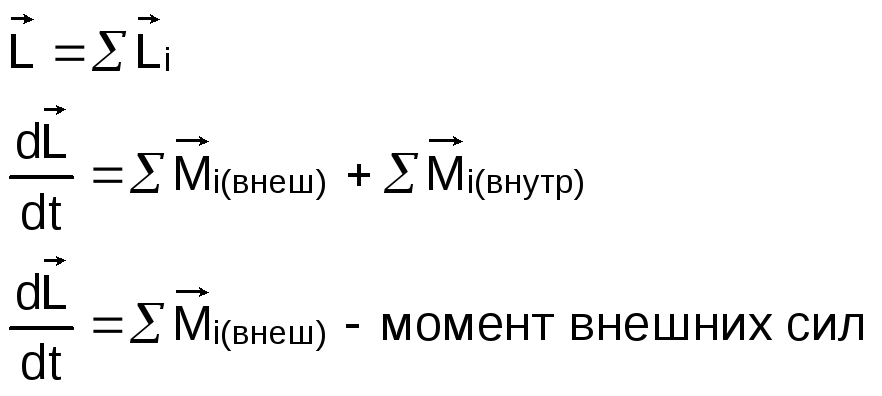
Приращение момента импульса равняется импульсу суммарного момента силы за время t
В![]() НИСО момент внешних сил будет складываться
из моментов силы взаимодействия и
момента инерции. Все моменты определяются
относительно какой-то точки
НИСО момент внешних сил будет складываться
из моментов силы взаимодействия и
момента инерции. Все моменты определяются
относительно какой-то точки
М![]() омент
импульса изолированной системы не
изменяется при любых процессах,
происходящих внутри данной системы.
омент
импульса изолированной системы не
изменяется при любых процессах,
происходящих внутри данной системы.
Рассмотрим проекцию L
С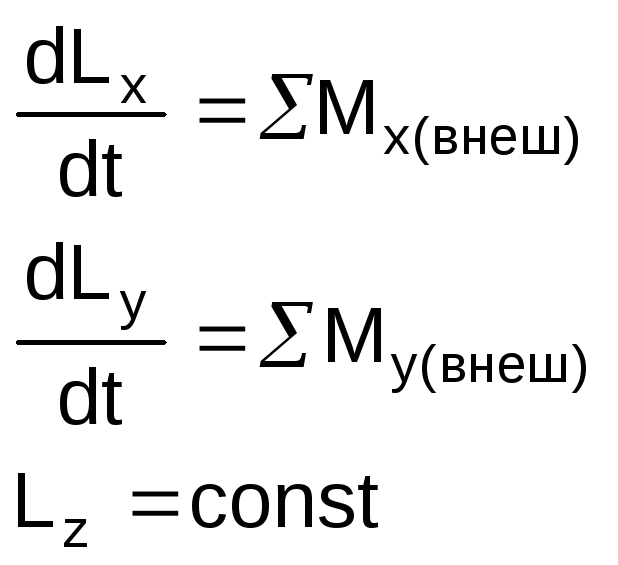 истема
изолирована относительно оси z
истема
изолирована относительно оси z
Пример выполнения закона сохранения момента импульса
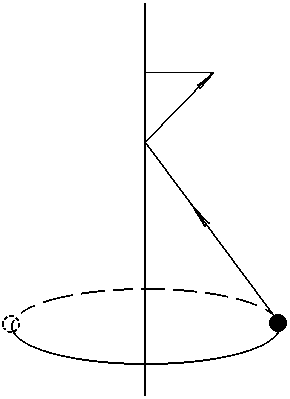
Н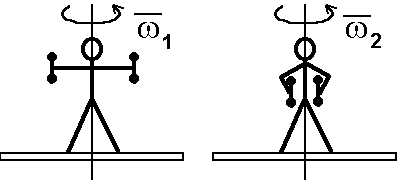 апример
Скамья Жуковского
апример
Скамья Жуковского
![]() Закон
сохранения момента импульса выполняется
для немеханических процессов (где
неприменимы законы Ньютона)
Закон
сохранения момента импульса выполняется
для немеханических процессов (где
неприменимы законы Ньютона)