
- •Лекция 9 Функции случайных величин
- •Задачи изучения функций св
- •Числовые характеристики функций случайных величин
- •Пример функции дискретной св
- •Интегральные числовые характеристики функции одной св
- •Пример 1: средняя проекция стержня при пространственном беспорядочном вращении
- •Числовые характеристики функции нескольких св
- •Пример 2: средняя проекция стержня при пространственном вращении
- •Пример 3: средняя площадь проекции параллелепипеда в пространственном вращении
- •Числовые характеристики линейных функций св
- •Мо и дисперсия полилинейной функции
- •Мо и дисперсия произведения св
- •Мо и корреляционная матрица векторной линейной функции
- •Пример 4: дисперсия суммарной ошибки в однократной коррекции
- •Метод линеаризации функций
- •Определение характеристик рассеивания
- •Аналитические методы определения характеристик рассеивания
- •Экспериментальное определение характеристик рассеивания
- •Имитационное моделирование рассеивания
- •Полунатурное моделирование рассеивания
- •Законы распределения функций случайных величин
- •Функция распределения монотонных функций св
- •Пример 5: способ получения реализаций св с заданным законом распределения
- •Плотность распределения монотонных функций св
- •Пример 6: закон распределения проекции стержня
- •Пример 7: закон распределения проекции стержня
- •Распределение немонотонных функций св
- •Пример 8: распределение нормальной ошибки с однократной коррекцией
- •Другие модели однократной коррекци
- •Пример 8: распределение промаха после однократной коррекци
- •Пример 9: одномерное перекрытие
Другие модели однократной коррекци
Пример 8: распределение промаха после однократной коррекци
![]() в
картинной плоскости подчиняется закону
Рэлея с параметром .
Коррекция промаха на величину a
имеет смысл, если промах превышает
допустимую величину
( < a).
Суммарный промах после условной коррекции
T
можно записать как функцию R:
в
картинной плоскости подчиняется закону
Рэлея с параметром .
Коррекция промаха на величину a
имеет смысл, если промах превышает
допустимую величину
( < a).
Суммарный промах после условной коррекции
T
можно записать как функцию R:
 .
.
Чтобы найти оптимальные значения a и , построим обратную функцию (r, a, ) согласно рис. 9.7

и выполним подстановку в (9.24):

|
x
y
a |
|
С помощью электронной формулы f_Rayl построим графики функции fR (рис. 9.9). Другие модели однократной коррекции рассмотрены в [1] .
|
|
Пример 9: одномерное перекрытие
|
|
|
Рис. 9.10. Перекрытие полосы |

В интервалах a<|x|<b функция (x) = b – |x| имеет двузначную обратную (y) при 0 < y < d:

![]()
Выполнив подстановку в (10.24), получим плотность распределения величины линейного перекрытия внутри интервала [0, d]:
fY(y) = fX(y – b) + fX(b – y), 0 < y < d.
Функцию распределения FY(y) внутри интервала [0, d] с учетом того, что события (Y<y) и (Y<1(y)) + (Y>2(y)) эквивалентны:

Воспользовавшись стандартной функцией нормального распределения, получим:
![]()
На концах интервала FY(0) = 0, FY(d+) = 1. Значит, в этих точках функция распределения имеет разрывы первого рода:

|
|
|
Рис. 9.11. Распределение линейного пререкрытия |
>> X=Norm_1(10,15);d=30;h=50;b=(h+d)/2;y=0:d;
>> f=f(X,y-b)+f(X,b-y); F=fun(X,y-b)+1-fun(X,b-y);
>> plot(y,f*30,[-0.1, y, d*1.0001, d*1.1],[0,F,1,1]), grid
Контрольные вопросы
-
На чем основан практический интерес к функциям случайных величин?
-
Как вычислить числовые характеристики фунуции случайных величин, не располагая ее законом распределения?
-
Система n случайных величин характеризуется вектором математических ожиданий M и корреляционной матрицей K. Как найти дисперсию суммы этих случайных величин?
-
Как выразить дисперсию объема параллелепипеда через числовые характеристики его независимых случайных размеров?
-
Как можно вычислить математическое ожидание и дисперсию слабо нелинейной функции Y = (X1, …, Xn) системы n случайных величин?
-
Каким соотношением связана плотность распределения монотонной функции случайной величины с законом распределения аргумента?
-
Запишите в общем виде выражение, связывающее плотность распределения немонотонной функции случайной величины с законом распределения аргумента.
-
Запишите в общем виде выражение для функции распределения системы двух случайных величин.
ПРИЛОЖЕНИЕ 9
Листинг 9.1. Файл-функция Para2_Distrib для построения закона распределения случайной площади проекции параллелепипеда:
function [Y,F]=Para2_Distrib(A,B,C)
topt=atan(B/C);
yopt=B*sin(topt)+C*cos(topt);
fopt=atan(A/yopt);
yopt=A*sin(fopt)+yopt*cos(fopt);
Y=linspace(A,yopt+3,300);
F=[];
for y=Y
F(end+1)=Para2_Proect_(y, A,B,C);
end
%
function out=Para2_Proect_(y, A,B,C)
out=0;
T=linspace(0,pi/2,100); dt=T(2)-T(1);T=T(2:end);
for t=T
b=B*sin(t)+C*cos(t);
ab2=A^2+b^2;
D=A^2*y^2-ab2*(y^2-b^2);
f2=0;
if D>0
D=sqrt(D);
f1 = (A*y-D)/ab2;
f2 = (A*y+D)/ab2;
if f1>0 out=out+f1; end
end
out=out+(1-f2);
end
out=out*2/pi*dt;
Листинг 9.2. Файл-функция Mid_S_Stat для построения статистического закона распределения случайной площади проекции многогранника:
function [U,F,f,maxW,L]=Mid_S_Stat(A,N,Gr)
if nargin<2 N=100000;end
s=rand(N,1)*2-1; s1=sqrt(1-s.^2);
v=rand(N,1)*2*pi;
D=[s1.*cos(v), s1.*sin(v), s];
n=size(A,1);W=0;L=zeros(N,1);
for i=1:n
d=D.*repmat(A(i,1:3),N,1); d=sum(d,2);
d(d<0)=0;
if nargout>4 L=max([L,d],[],2); end
d=d*A(i,4);
W=W+d;%disp(mean(sum(d,2)))
end
[f, F, U] = SDL(W,50); maxW=max(W);
Листинг 9.3. Скрипт-файл Lect9 для формирования матрицы проекций 8-гранника:
salfa=sin(alfa);calfa=cos(alfa);
h=c/(2*salfa);h1=sqrt(b^2+c^2)/2;a1=a-c*calfa/salfa;
St=b*h/2;Sb=(a+a1)/2*h1;
beta=atan(c/b);
nob=[0 1 1; 0 1 -1; 0 -1 1; 0 -1 -1];
not=[1 0 1; 1 0 -1; -1 0 1; -1 0 -1];
A=[nob,ones(4,1)].*repmat([0 cos(beta) sin(beta) Sb],4,1);
A=[A;[not,ones(4,1)].*repmat([salfa 0 calfa St],4,1);
БЭСПиБП.9.
Функции случайных величин





 Рис.
9.8
Рис.
9.8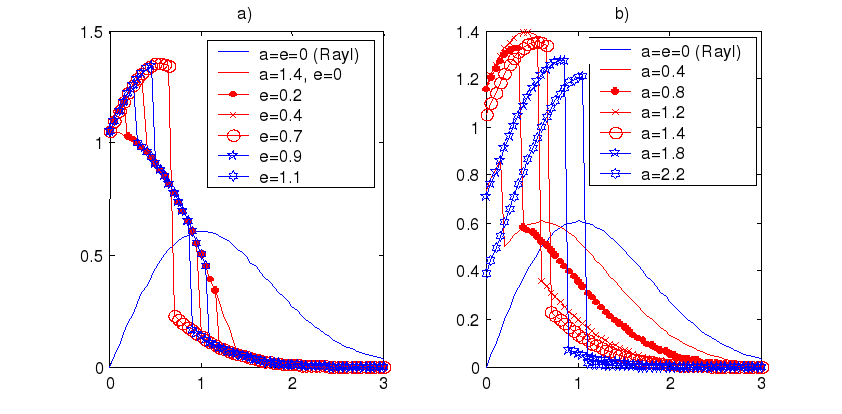 Рис. 9.9
Рис. 9.9
