
- •1. Основные этапы разработки программных продуктов
- •1.1 Постановка задачи
- •Словесная формулировка
- •Формульная постановка задачи
- •1.2 Создание программного продукта
- •1.2.1.Формирование математической модели
- •Формирование исходных данных
- •Составление расчётных зависимостей
- •Правила формирования математической модели.
- •1.2.2.Алгоритмизация задачи
- •Выбор метода решения
- •Составление алгоритма решения
- •Программирование задачи
- •1.2.3. Реализация программного продукта
- •1.2.4. Работа с результатами
- •1.2.5.Анализ результатов решения
- •1.2.6.Принятие решения
- •1.2.7.Составление технической документации
- •1.3.Полная обработки задачи пользователя
- •1.4.Обеспечение эффективности разработки программных продуктов
- •2.5 Идентификаторы
- •2.6 Описание операций
- •2.6.1 Унарные операции
- •2.6.2 Бинарные операции
- •2.6.3 Пунктуаторы
- •Программирование простых ветвлений
- •4.1.5. Программирование задачи
- •Правила составления и использования
- •4.1.5.2. Операторы условной передачи управления
- •Укороченный оператор условного перехода
- •Правила записи и выполнения
- •Условная операция
- •Технология программирования арифметических циклов
- •Циклы с аналитическим заданием аргумента
- •Постановка задачи
- •Формирование математической модели
- •Выбор метода решения
- •Составление алгоритма
- •Оператор цикла с предусловием
- •Правила записи и выполнения
- •Оператор цикла с постусловием
- •Правила записи и выполнения
- •Оператор пошагового цикла for
- •Правила записи и выполнения
- •Программа по алгоритму цикла с предусловием
- •Программа по алгоритму цикла с постусловием
- •Программа по алгоритму цикла с параметром
- •Циклы с табличным заданием аргумента
- •Описание массивов
- •Описатель имя[размер];
- •Обозначение элементов массива
- •Имя[индекс]
- •Описатель имя[разм_1] …[разм_i]… [разм_n];
- •Постановка задачи
- •Математическая формулировка
- •Выбор метода решения
- •Составление алгоритма решения
- •Алгоритмизация структурой цикла с предусловием
- •Алгоритмизация структурой цикла с постусловием
- •Алгоритмизация структурой цикла с параметром
- •Программирование задачи
- •Описание массивов
- •Обозначение элементов массива
- •Составление программ решения задачи
- •Улучшение качества программных продуктов
- •Организация ввода-вывода Использование укороченных спецификаторов
- •Ввод переменных
- •Вывод переменных
- •Организация ввода в диалоге
- •Варианты ввода массивов
- •Оформление выводимых величин
- •Управление выполнением программ Использование составных присваиваний
- •Выбор устройства вывода
- •Повторение расчётов
- •Приостановка вывода
- •Очистка экрана
- •Позиционирование курсора
- •Пример улучшения качества
- •Программирование с использованием подпрограмм
- •Имя (фактические параметры)
- •Подпрограмма с одним результатом
- •Формирование математической модели
- •Выбор метода решения
- •Составление алгоритма решения
- •Программирование задачи
- •Составление алгоритма решения
- •Программирование задачи
- •Составление алгоритма решения
- •Программирование задачи
- •Подпрограмма с результатом – массивом
- •Постановка задачи
- •Математическая формулировка
- •Выбор метода решения
- •Составление алгоритма решения
- •Программирование задачи
- •Обработка текстовой информации в Си Символьные строки
- •Определение значения символьной строки
- •Массивы строк
- •Ввод строки
- •Выделение памяти
- •Функции ввода символьной строки
- •Функция ввода символьной строки gets( )
- •Функция ввода символьной строки scanf( )
- •Преобразование символьных строк
- •Функция atoi( )
- •Функция atol( )
- •Функции atof( ) и atold( )
- •Методика ввода числовых данных с использованием функции gets( )
- •Вывод строки
- •Вывод строки функциями printf( ) и fprintf( )
- •Вывод строки функциями puts( ) и fputs( )
- •Перевод чисел в формат символьной строки
- •Обработка символьных строк
- •Определение длины строки
- •Объединение строк
- •Копирование строк
- •Сравнение строк
- •Функции по работе с датой и временем.
- •Структуры.
- •Работа с дисками.
- •Ввод-вывод потока.
- •Открытие потока.
- •Объектно−ориентированное программирование
- •Классы ObjectWindows
- •Приложение коды клавиш
- •Краткий справочник по Си
- •Оператор вывода на принтер
- •Структура оператора
- •Структура оператора
- •Структура оператора
- •Библиографический список
Формульная постановка задачи
Наряду со словесной возможна математическая (формульная) постановка задачи.
Математическая постановка представляет собой конкретные зависимости вычисления искомых функций с указанием исходных данных.
Математическая формулировка может быть выполнена для всей задачи в целом или являться частью словесной.
В первом случае задача, как правило, чисто абстрактная. Входные данные могут задаваться отдельно или численными значениями в расчётных зависимостях. При этом они не имеют физической сути и, естественно, размерностей.
Рассмотрим две задачи с математической формулировкой.
Пример 1.4. Рассчитать значение функции
![]() ,
,
если
a=12; b= -9,2;
x=2,75;
![]() =0,76.
=0,76.
Пример
1.5. Рассчитать корни квадратного уравнения
![]() по стандартной зависимости
по стандартной зависимости
![]() , если a=1,4; b=11,2;
c= -7,8.
, если a=1,4; b=11,2;
c= -7,8.
В примере 2.4 формулировка практически полностью представлена одной математической зависимостью, в примере 2.5 – математическая формулировка является частью словесной.
Типичными примерами частично математически сформулированных, являются задачи расчета площадей (объемов) геометрических фигур.
Пример
1.6. Рассчитать площади круга (в см2)
по известной зависимости
![]() ,
если диаметр изменяется от 35 см до 120 см
с шагом 15 см.
,
если диаметр изменяется от 35 см до 120 см
с шагом 15 см.
Каждая из законченных постановок задач позволяет перейти к следующему этапу – созданию программного продукта.
1.2 Создание программного продукта
Любой программный продукт (программное средство) создаётся человеком. В зависимости от назначения и сложности программного продукта его разработка требует разного уровня профессионализма. Системное ПО, как правило, создаётся профессионалами высшей квалификации – системными программистами. Прикладные программы в принципе могут создаваться специалистами любой области знаний, владеющими основами программирования на языках высокого уровня. Однако сложные прикладные программы по заказу разрабатываются профессионалами – прикладными программистами.
Независимо от степи сложности задачи и квалификации программиста создание программного продукта выполняется с использованием стандартных методик.
Создание программного продукта (предмашинная подготовка задачи) – этап последовательного преобразования задачи в программный продукт.
Программный продукт есть оформление задачи в виде доступном ЭВМ.
Создание программных продуктов базируется на принципах математизации, алгоритмизации и программирования. В общем виде математизация подразумевает создание математической модели задачи, алгоритмизация позволяет выбрать метод её решения и оформить его в подетальном виде, понятном человеку (алгоритмом), программирование позволяет преобразовать полученный алгоритм в форму доступную ЭВМ.
Степень детализации предмашинной подготовки может быть различной. Укрупнённая схема создания программного продукта имеет вид (рис. 2.2).
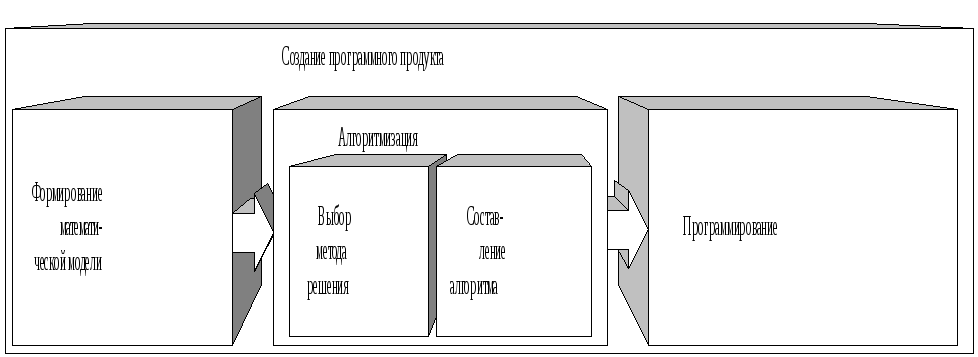
Рис. 1.2. Схема создания программного продукта
Рассмотрим выделенные элементы с увеличенной степенью детализации.
1.2.1.Формирование математической модели
Создание математической модели – этап преобразования словесной формы записи (заданного математического описания) задачи в универсальную стандартизованную математическую форму.
Для сложных задач пользователю рекомендуется выполнять этот этап с помощью математика или программиста. При этом существенно уменьшается число возможных ошибок.
Математическая модель (модель задачи) – представление задачи в математически универсальном (формализованном) виде.
Математическая модель (ММ) представляет собой совокупность зависимостей, описывающих входные (исходные) данные, а также их связи в вычислениях промежуточных и конечных данных (результатов).
Математическая модель предназначена для определения значений всех поименованных данных (объектов задачи) напрямую или аналитически.
Основные требования к математической модели:
-
адекватность (максимальное соответствие) поставленной задаче;
-
универсальность (возможность описания широкого класса однотипных задач).
Представим модель задачи с увеличенной степенью детализации (рис. 2.3).
Основные компоненты верхнего уровня математической модели – входные данные и расчетные зависимости. Исходя из этого, формулировка математической модели должна выполняться в два этапа:
-
формирование входных (исходных) данных;
-
получение конечных (промежуточных) данных составлением расчётных зависимостей.
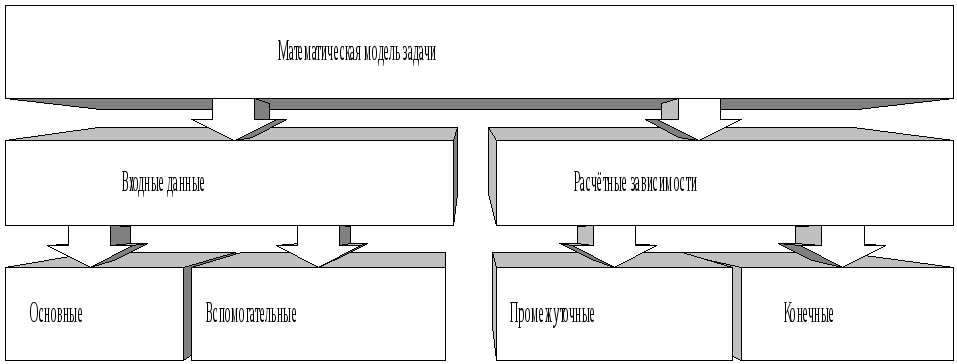
Рис. 1.3. Структура математической модели
