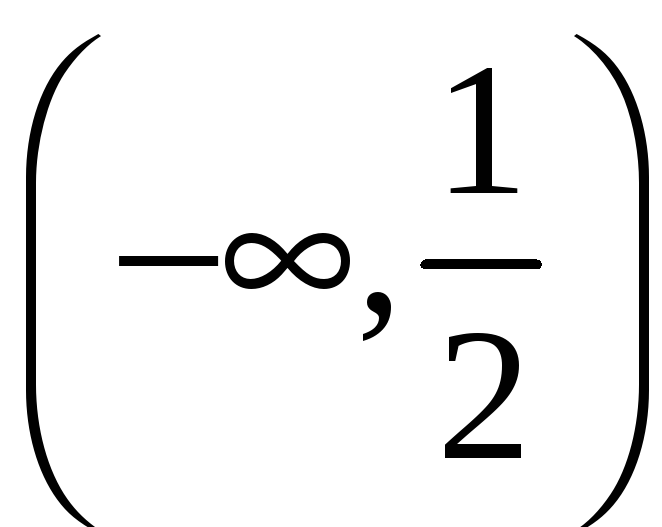2Способ (с помощью второй производной)

Найдём вторую производную:

;

Найдём значение второй производной в критических точках.

.

.

Значит, прибыль в точке максимальная.

Найдём значение максимальной прибыли:

.

3.9. Требуется изготовить коническую воронку с образующей, равной 15 см. Какова должна быть высота воронки, чтобы её объём был наибольшим?

 Пусть , тогда:

.

Объём:

.

;

Найдём критические точки функции:

;

;

;

.

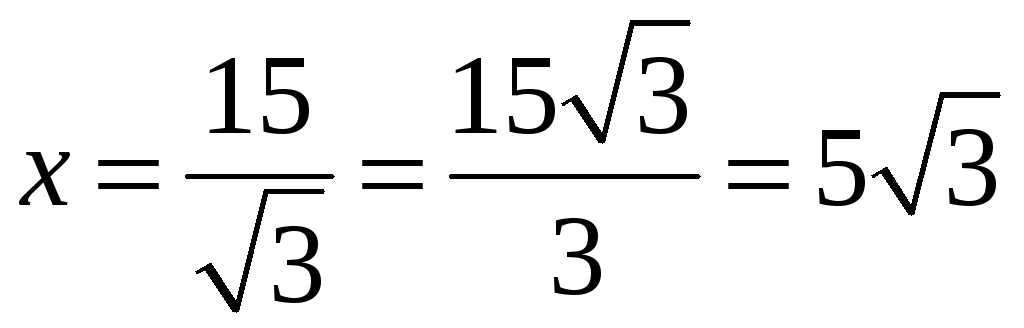Получили, чтобы объём воронки с образующей 15 см был наибольшим, высота её должна быть равной см. 

4. Выпуклость функции и точки перегиба.

Достаточные условия выпуклости.

Пусть существует на отрезке , а — на интервале . Тогда:

1) если

при всех ,

то функция выпукла вниз на отрезке .

2) если

при всех ,

то функция выпукла вверх на отрезке .

Необходимое условие наличия точки перегиба.

Если — точка перегиба функции и если функция имеет в некоторой окрестности точки вторую производную, непрерывную в точке , то

.

Достаточные условия наличия точки перегиба.

1) Если функция непрерывна в точке , имеет в этой точке конечную или бесконечную производную и если функция меняет знак при переходе через точку , то — точка перегиба функции .

2) Если , , то — точка перегиба функции .

Примеры

4.1. Показать, что функции выпукла вверх на всей области определения.

 Вычислим вторую производную

.

Область определения функции

множество . Очевидно, для любых .

4.2. Найти точки перегиба линии , .

 Вычислим вторую производную параметрически заданной функции оп формуле

.

Так как , , , , получаем

.

Разобьем ось точками , , на три интервала. На каждом из этих интервалов вторая производная сохраняет знак. Составим таблицу значений , и знака на соответствующих интервалах.

	От до

Таким образом, точками перегиба будут и .

4.3. Найти точки перегиба и интервалы выпуклости функции

 Вычисляя производные

, .

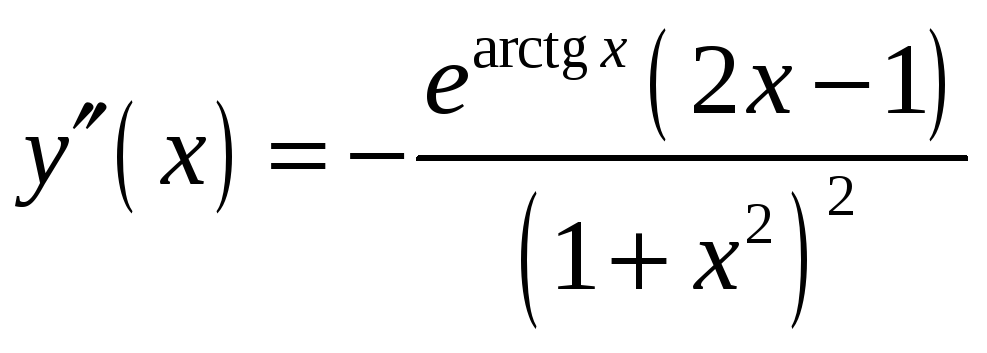Составим таблицу постоянства знаков второй производной.

		Выпукла вниз
		Точка перегиба
		Выпукла вверх

Таким образом, точка - точка перегиба.

4.4. Найти точки перегиба линии , .

 Вычислим вторую производную, параметрически заданной функции по формуле

.

Так как , , , , получаем

.

Точки, в которых определяются из уравнения , и нетрудно убедиться, что в , , вторая производная меняет знак, следовательно, эти точки – точки перегиба.

4.5. Показать, что точки перегиба линии лежат на линии .

 Точки пересечения линий удовлетворяют уравнению

. (*)

Покажем, что точки перегиба линии удовлетворяют этому уравнению. Вычисляя вторую производную и приравнивая ее нулю получаем уравнение

или , (**)

так как . Подставляя (**) в (*) получаем тождество

.