3.2. Передача силового навантаження від жорсткого диска до криволінійного отвору нескінченної пластинки.

Нехай в криволінійний отвір виду (2.1) нескінченної пластинки запресовано з натягом абсолютно жорсткий диск такої ж форми (рис.2.5). В центрі диска прикладено силу , яка діє вздовж осі симетрії отвору. Посадку диск в отвір пластинки здійснено з гарантованим натягом, тому як і в попередній задачі зона контакту замкнена, або контакт порушується в одній (еліптичний отвір) чи двох (трикутний отвір) точках.

3.2.1. Інтегродиференціальні рівняння задачі. Систему прямокутних координат вибираємо так, як показано на рис. 2.5.

Граничні умови задачі виберемо у вигляді рівності кривин в зоні контакту. При відсутності тертя між пластинкою і диском ці умови на підставі (2.49) можна записати у вигляді

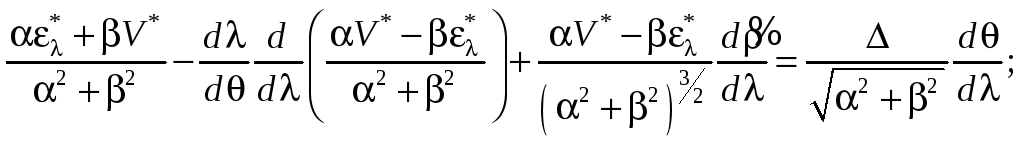
(3.15)

Величини на контурі отвору визначаються за формулами (2.2), (2.4), в яких при заданому навантаженні необхідно прийняти .

(3.16)

Якщо підставити (3.16) в граничні умови (3.15), то одержимо систему двох інтегродиференціальних рівнянь для визначення функцій . Крім системи (3.15), (3.16) повинна виконуватися умова рівноваги штампа

(3.17)

Співвідношення (3.15) – (3.17) визначають математичну модель розглядуваної задачі.

3.2.2. Наближений розв’язок задачі. Оскільки зона контакту між пластинкою і диском неперервна, то наближений розв’язок задачі (3.15) – (3.17) будемо шукати у вигляді скінченних рядів Фур’є.

(3.18)

Тут враховано симетричність задачі відносно осі Ох.

Підставляючи (3.18) в співвідношення (3.16), (3.17) з врахуванням (3.11), одержимо після обчислення відповідних інтегралів

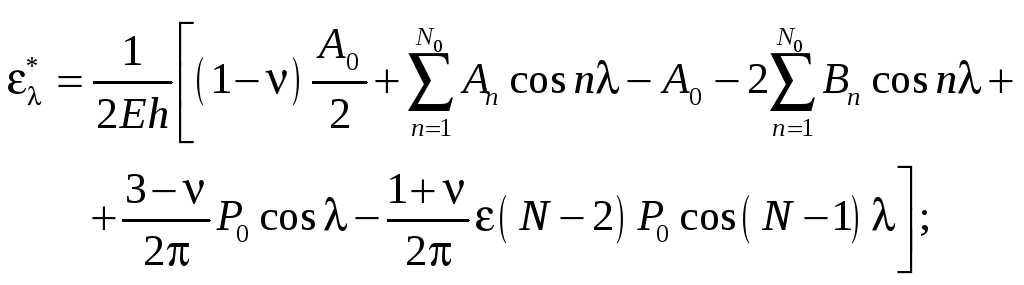
(3.19)

Співвідношення (3.19) разом з граничними умовами (3.15) визначають систему функціональних рівнянь для визначення сталих, що входять до (3.18). Якщо в цій системі порівняти ліві і праві частини при , то одержимо систему лінійних алгебраїчних рівнянь для визначення .

Для визначення мінімального натягу , при якому можливе розмикання контакту лише в одній точці , необхідно до системи (3.15), (3.19) приєднати умову рівності нулю в цій точці контактного тиску (3.14).

Методика визначення кута така ж, як і в попередній задачі.

При одержимо розв’язок контактної задачі про тиск абсолютно жорсткого диска на круговий отвір нескінченної пластинки.

Розділ 4 неповний контакт жорсткого диска з криволінійним отвором нескінченної пластинки

В профільних з’єднаннях валів і дисків, які передають силове навантаження і обертальний момент, відбувається відносне їх зміщення і поворот, тому щільний контакт відбувається в обмежених зонах. Площа цих зон тим більша, чим менший зазор і більше силове та моментне навантаження.

У даному розділі розглядаються контактні задачі для нескінченної пластинки з криволінійним отвором, в який вставлено із нульовим зазором або натягом гладкий або з кутовими точками абсолютно жорсткий диск, який передає до пластинки зосереджену силу або обертальний момент. Будуються математичні моделі задач про неповний контакт циліндричних тіл з гладкими і ребристими поверхнями.