2.2. Круглий ізотропний диск

Допустимо, що на контурі або його частині круглого ізотропного диска радіусом задано нормальні і дотичні зусилля як функції точок цього контуру, головний вектор яких дорівнює нулю. В центрі диска прикладено пару сил з моментом (рис. 2.2). Середня площина диска віднесена до декартової і полярної систем координат з полюсом в центрі диска.

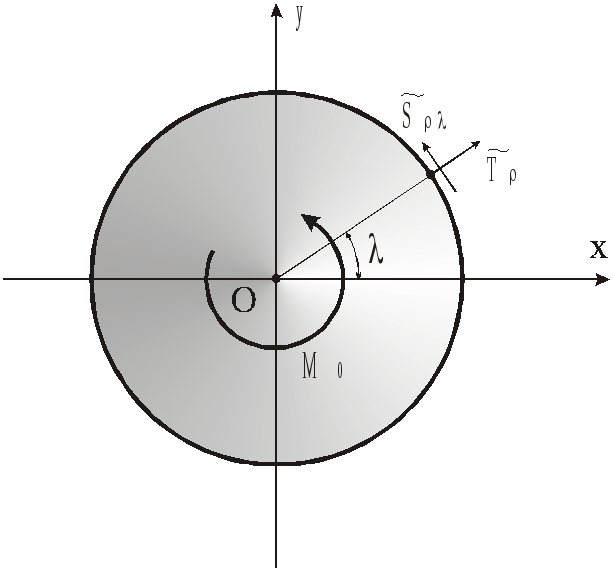
Рис. 2.2. Схема навантаження диска

Деформації контуру при заданому навантаженні визначаються за формулами

;

, . (2.17)

Тут , – модуль Юнга і коефіцієнт Пуассона матеріалу диска; - товщина диска.

Кільцеві зусилля на контурі диска визначаються із співвідношення

. (2.18)

Гранична умова першої основної задачі плоскої теорії пружності для кругового диска запишеться так

, (2.19)

де , – комплексні потенціали Мусхелішвілі; – комплексна стала;

. (2.20)

Помноживши (2.19) на і проінтегрувавши по контуру , одержимо для заданого навантаження

. (2.21)

Запишемо граничну умову другої основної задачі, яка має вигляд

. (2.22)

Тут ; .

Додаючи граничні умови (2.19), (2.22), знаходимо на контурі

. (2.23)

Застосовуючи до (2.21) формули Сохоцького-Племеля і підставляючи отримані результати в (2.23) з урахуванням співвідношення (2.13), одержимо вирази для компонент вектора зміщення контурних точок диска

, (2.24)

де , , – дійсні сталі.

У формулах (2.24) враховано, що функція (2.21) визначає компоненти вектора зміщення з точністю до зміщення диска як жорсткого цілого.

Крім співвідношень (2.17)-(2.24) повинні виконуватися умови граничної рівноваги диска

; . (2.25)

2.3. Граничні умови контактних задач для нескінченної пластинки з криволінійним отвором і жорсткого диска

2.3.1. Допустимо, що в криволінійний отвір виду (2.1) нескінченної пластинки запресовано з натягом абсолютно жорсткий диск такої ж форми (рис. 2.3). Вважаємо, що величина має порядок пружних зміщень.

Рис. 2.3. Схема взаємодії пластинки і диска

Рівняння контура диска у вибраній системі координат на підставі (2.1) має вигляд

, . (2.26)

Будемо умовно вважати, що до спряження з пластинкою диск мав форму та розміри отвору і його контур визначався рівнянням

. (2.27)

Після того, як диск був вставлений в отвір пластинки без зазору і натягу, він почав „збільшуватися” до виду (2.26).

Граничні умови контакту пластинки і диска приймаємо у вигляді рівності нормальних зміщень пластинки і диска

, . (2.28)

Якщо в зоні контакту наявні сили тертя, то в цьому випадку необхідно задати закон зміни дотичних напружень

, . (2.29)

На підставі (2.16) можна записати

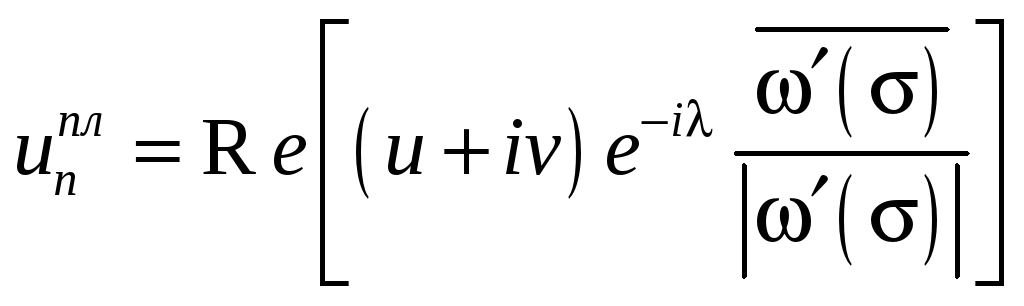. (2.30)

Після певних перетворень із (2.30), одержимо

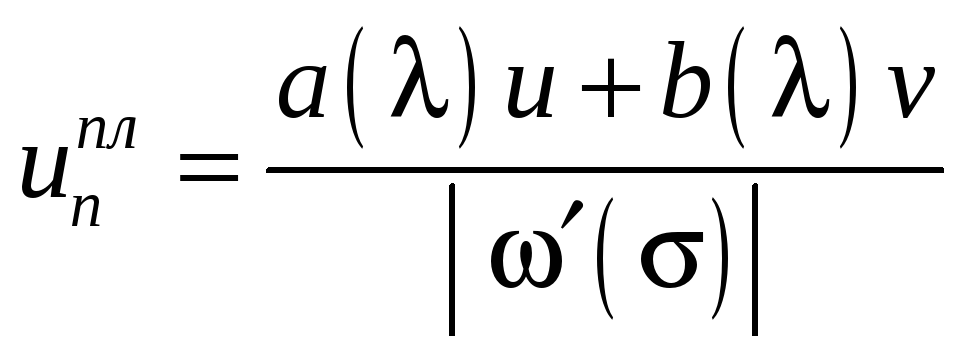, (2.31)

де ;

.

Аналогічно знаходимо вираз для нормального “зміщення” диска

. (2.32)

Тут , – компоненти вектора “зміщення” контурних точок диска. Їх визначаємо за формулою

. (2.33)

Розділяючи в (2.33) дійсну і уявну частини, одержимо

;

.

Враховуючи останні співвідношення із (2.32), після певних перетворень отримаємо

. (2.34)

Підставляючи (2.34), (2.31) в (2.28), одержимо граничні умови задачі про напружену посадку жорсткого диска виду (2.26) в криволінійний отвір нескінченної пластинки

;

, . (2.35)

2.3.2. Нехай в криволінійний отвір пластинки вставлено без зазору і натягу () жорсткий диск, в центрі якого прикладено пару сил з моментом . Внаслідок цього диск повернеться на кут і вступить в контакт з частиною контуру пластинки. Образом контура диска при повороті на кут буде крива

. (2.36)

На рис. 2.4 її положення для еліптичного отвору зображене суцільною лінією.

За аналогією з (2.33) запишемо вираз для компонент зміщення контурних точок диска

.

Після розділення в останньому співвідношенні дійсних і уявних частин знаходимо

;

. (2.37)

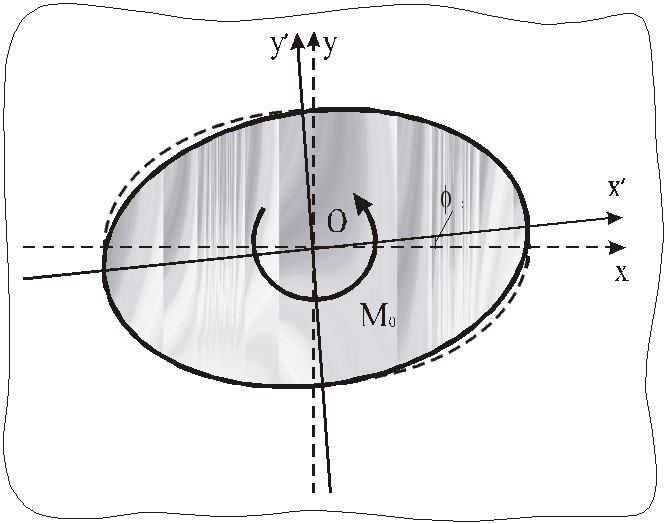
Рис. 2.4. Схема взаємодії пластинки і диска

Підставляючи , із (2.37) в (2.32) замість , , отримаємо

(2.38)

З урахуванням (2.38) граничні умови (2.28), (2.29) даної задачі запишуться у вигляді

, , (2.39)

де , – відповідно зона контакту і її образ при відображенні (2.1).

Для визначення кута повороту диска служить умова його граничної рівноваги

. (2.40)

Формула (2.38) відрізняється першим доданком в правій частині від відповідної формули для еліптичного отвору, одержаної Мусхелішвілі М.І. Таким же доданком будуть відрізнятися праві частини граничних умов (2.39). Оскільки для малих деформацій , , тому доданками з множником в (2.38) будемо нехтувати. Числові розрахунки контактних зусиль в модельних задачах, які проведені для цих випадків, практично співпадають. Це означає, що граничні умови (2.39) можна записати у вигляді

; ,

. (2.41)

2.3.3. Розглянемо комбінацію задач, наведених в попередніх пунктах, і будемо вважати, що в криволінійний отвір виду (2.1) нескінченної пластинки запресовано з натягом жорсткий диск такої ж форми. В центрі диска прикладено пару сил з моментом . Оскільки „збільшення” і поворот диска є лінійні перетворення, тому

. (2.42)

Якщо сили тертя в зоні контакту задані законом Кулона, то

, , (2.43)

де – коефіцієнт тертя ковзання.

Підставляючи (2.42), (2.34), (2.38) в граничну умову (2.28) при та врахувавши співвідношення (2.43), одержимо граничні умови задачі про передачу обертального моменту від абсолютно жорсткого диска, запресованого в криволінійний отвір нескінченної пластинки

;

. (2.44)

В залежності від величини зона контакту може бути замкнена або розімкнена. Якщо , то маємо задачу про напружену посадку жорсткого диска з гарантованим натягом, при якому зона контакту охоплює весь контур . При на контурі , крім зон контакту, наявні зони відставання диска від пластинки. Величина визначає мінімальний натяг, при якому контакт між пластинкою і диском порушується тільки в одній точці. Покладаючи в (2.44) , одержимо граничні умови задачі для пластинки з круговим отвором.

2.3.4. Допустимо, що в криволінійний отвір виду (2.1) пластинки запресовано з натягом абсолютно жорсткий диск такої ж форми (рис. 2.5). Вважаємо, що величина має порядок пружних зміщень. Тут – радіус кривини диска. В центрі диска прикладено силу , яка діє вздовж осі симетрії отвору. При одержуємо посадку диска із натягом, – із зазором. Тертям в зоні контакту пластинки і диска нехтуємо.

Граничні умови задачі вибираємо у вигляді рівності кривин пластинки і диска в зоні контакту

(2.45)

Рис. 2.5. Розрахункова схема задачі

Формула для обчислення кривини деформованого контуру пластинки має вигляд

, (2.46)

причому для контуру (2.1) мають місце залежності

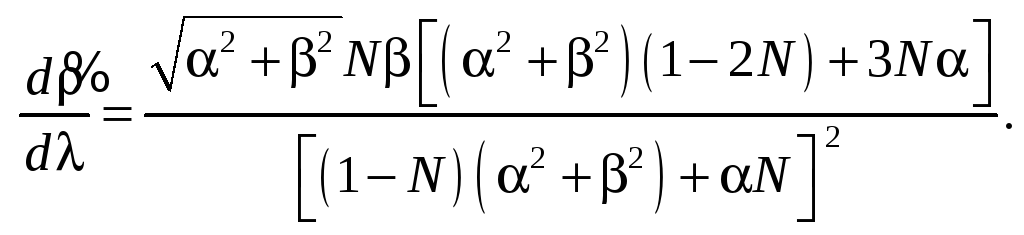(2.47)

З врахуванням (2.5) формула (2.46) набуває вигляду

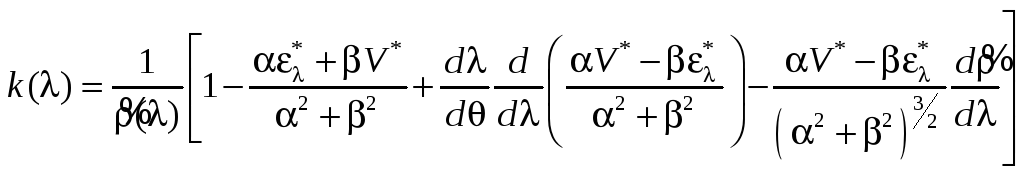. (2.48)

Тоді граничні умови задачі (2.45) можна перетворити так

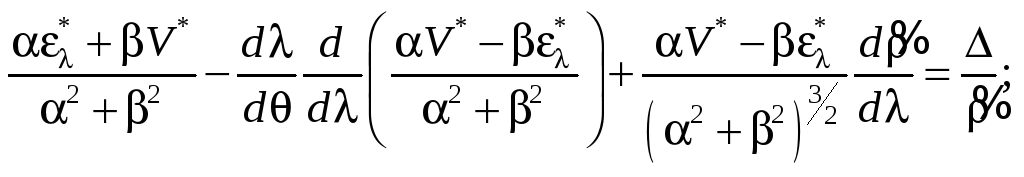
(2.49)

Зауважимо, що у випадку жорсткого штампа з кутовими точками граничні умови (2.49) використовувати не можна, бо в кутових точках диска кривина не визначена. У цьому випадку граничні умови слід вибирати у вигляді рівності нормальних зміщень контурних точок пластинки і штампа.