
- •Механіка суцільного середовища
- •Кінематика суцільного середовища
- •Основні поняття і задачі механіки суцільного середовища
- •Способи задання руху суцільного середовища
- •Розділ 2 елементи гідродинаміки
- •2.1. Основні поняття і формули векторного аналізу
- •2.2. Рівняння неперервності руху ідеальної рідини
- •2.3. Рівняння Ейлера
- •2.4. Гідростатика
- •2.5. Умова відсутності конвекції
- •2.6. Рівняння Бернуллі
- •Основи теорії пружності (теорія деформації)
- •3.1. Вектор зміщення і деформований стан
- •3.2. Тензор деформації
- •3.3. Перетворення компонент тензора деформації при заміні системи відліку
- •3.4. Головні напрямки тензора деформації. Головні осі і головні деформації
- •3.5. Визначення компонент вектора зміщення через компоненти тензора деформації
- •3.6. Визначення зміщень через компоненти тензора відносного зміщення
- •Основи теорії пружності (теорія напружень)
- •4.1 Зовнішні сили. Вектор напруження. Напружений стан тіла
- •4.2. Тензор напружень
- •4.3. Диференціальні рівняння рівноваги пружного тіла. Симетричність тензора напружень
- •4.4. Перетворення компонент тензора напружень при повороті системи координат
- •4.5. Головні напруження і інваріанти тензора напружень
- •Основи теорії пружності (співвідношення між компонентами тензора напружень)
- •5.1. Узагальнений закон Гука
- •Основи теорії пружності (основні рівняння і задачі теорії пружності)
- •6.1. Основні рівняння теорії пружності
- •6.2. Основні задачі статики пружного тіла
- •6.3. Пряма і обернена задачі теорії пружності
- •6.4. Рівняння пружної рівноваги в зміщеннях
- •6.5. Основні рівняння в напруженнях
- •Застосовуючи до (6.32) оператор Лапласа, одержимо
- •6.6. Напівобернений метод Сен-Венана
- •6.7. Принцип Сен-Венана
- •Найпростіші задачі теорії пружності
- •Метод суперпозиції
- •Основи теорії пружності (плоска задача теорії пружності)
- •7.1. Плоска деформація
- •7.2. Плоский напружений стан
- •7.3. Узагальнений плоский напружений стан
- •7.4. Основні рівняння плоскої теорії пружності. Зведення до бігармонічної проблеми
- •7.5. Плоска задача в декартових координатах
- •Нехай функція напружень має вигляд полінома третього степеня
- •Виберемо функцію напружень у вигляді полінома четвертого степеня
- •Якщо розглядається друга гранична задача, то граничні умови мають вигляд
- •8.2. Зведення основної задачі до бігармонічної проблеми
- •8.3. Задачі, в яких напруження залежать тільки від
- •Задачі, в яких напруження залежать від і
- •Підставляючи (8.67) у (8.64), одержимо формули для напружень
- •Застосування функцій комплексної змінної до розв’язування задач плоскої теорії пружності
- •9.1. Комплексне подання функції напружень
- •Розглянемо основне рівняння плоскої теорії пружності
- •9.2. Комплексне подання компонент тензора напружень і вектора зміщень
- •9.3. Степінь визначеності і структура комплексних потенціалів
- •9.4. Перетворення рівнянь плоскої задачі теорії пружності при конформному відображенні
- •9.5. Двосторонній розтяг нескінченної площини з еліптичним отвором
- •Список літератури
Основи теорії пружності (теорія деформації)
3.1. Вектор зміщення і деформований стан
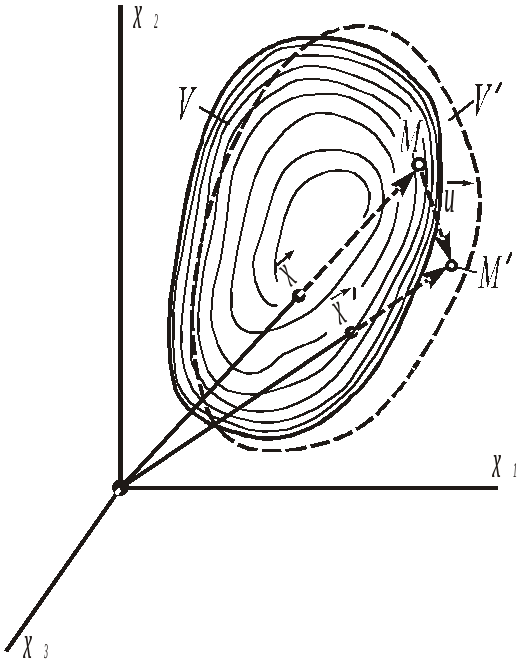
Під дією зовнішніх сил або внаслідок зміни теплового стану пружне тіло змінює свої розміри і форму, тобто деформується.
Нехай
тіло, як суцільне середовище, в початковому
стані (до прикладання зовнішнього
навантаження) займає в тривимірному
евклідовому просторі деякий об’єм
![]() .
Положення довільної точки
.
Положення довільної точки
![]() тіла, яку на відміну від геометричної
точки простору будемо називати
матеріальною точкою, визначається
радіус-вектором
тіла, яку на відміну від геометричної
точки простору будемо називати
матеріальною точкою, визначається
радіус-вектором
![]() з координатами
з координатами
![]()
![]() в декартовій системі координат
в декартовій системі координат
![]() .
.
Допустимо,
що в результаті деякого зовнішнього
впливу на тіло відбулося зміщення його
точок і тіло зайняло новий об’єм
![]() (об’єми
(об’єми
![]() і
і
![]() можуть мати спільні точки). При цьому
матеріальна точка
можуть мати спільні точки). При цьому
матеріальна точка
![]() зміститься в положення точки
зміститься в положення точки
![]() .
.
Вектор
![]() ,
який визначається початковим і кінцевим
положенням матеріальної точки
,
який визначається початковим і кінцевим
положенням матеріальної точки
![]() ,
називається вектором
її зміщення
(рис. 3.1).
,
називається вектором
її зміщення
(рис. 3.1).
Кожна
матеріальна точка
![]() зміщується в деяку іншу точку
зміщується в деяку іншу точку
![]() ,
за винятком окремих точок, наприклад
закріплених, які будуть спільними для
об’ємів
,
за винятком окремих точок, наприклад
закріплених, які будуть спільними для
об’ємів
![]() і
і
![]() .
При цьому тіло, зайнявши новий об’єм
.
При цьому тіло, зайнявши новий об’єм
![]() ,
за допущенням, залишається суцільним
середовищем. Тому координати
,
за допущенням, залишається суцільним
середовищем. Тому координати
![]() точок об’єму
точок об’єму
![]() ,
які залежать не тільки від зовнішнього
навантаження, але й від точки
,
які залежать не тільки від зовнішнього
навантаження, але й від точки
![]() ,
повинні бути неперервними і однозначними
функціями координат
,
повинні бути неперервними і однозначними
функціями координат
![]() ,
,
![]() ,
,
![]() точки
точки
![]() в стані
в стані
![]()
![]()
 . (3.1)
. (3.1)
Будемо
вважати, що функції (3.1) мають неперервні
похідні по всіх змінних
![]()
![]() .
Якщо при цьому якобіан
.
Якщо при цьому якобіан
![]() ,
то рівняння (3.1) можна розв’язати відносно
,
то рівняння (3.1) можна розв’язати відносно
![]()
Рис. 3.1
![]()
Компоненти
![]() вектора зміщення
вектора зміщення
![]() на підставі (3.1), (3.2) можуть бути виражені
або як функції
на підставі (3.1), (3.2) можуть бути виражені
або як функції
![]() ,
,
![]() ,
,
![]()
![]() , (3.3)
, (3.3)
або
як функції
![]() ,
,
![]() ,
,
![]()
![]() . (3.4)
. (3.4)
Спосіб
задання зміщень функціями (3.3), коли за
незалежні змінні приймаються координати
![]() матеріальної точки
матеріальної точки
![]() в початковому стані
в початковому стані
![]() ,
називається Лагранжевим.
Він прослідковує історію руху матеріальної
точки із положення
,
називається Лагранжевим.
Він прослідковує історію руху матеріальної
точки із положення
![]() в положення
в положення
![]() .
.
Інший
спосіб руху суцільного середовища з
допомогою функцій (3.4), в яких незалежними
змінними є координати
![]() точок
точок
![]() ,
називається способом
Ейлера.
,
називається способом
Ейлера.
В
теорії пружності застосовують спосіб
Лагранжа, який дозволяє визначити
зміщення фіксованої матеріальної точки
![]() ,
яке вона одержить з початкового положення
внаслідок зовнішньої дії на тіло.
,
яке вона одержить з початкового положення
внаслідок зовнішньої дії на тіло.
Перехід
тіла з початкового стану
![]() в новий стан
в новий стан
![]() можливий і внаслідок зміщення тіла, як
абсолютно твердого, тобто без зміни
відстаней між його точками. Таке зміщення
тіла називається жорстким
зміщенням.
можливий і внаслідок зміщення тіла, як
абсолютно твердого, тобто без зміни
відстаней між його точками. Таке зміщення
тіла називається жорстким
зміщенням.
Якщо
перехід тіла з початкового стану
![]() в новий стан
в новий стан
![]() відбувається внаслідок зміни відстаней
між його точками, то новий стан
відбувається внаслідок зміни відстаней
між його точками, то новий стан
![]() називається деформованим.
називається деформованим.
Очевидно,
що деформований стан тіла повністю
визначається, якщо будуть відомі функції
![]() .
.
Деформований
стан тіла, який визначається лінійними
функціями
![]() ,
називається однорідним.
Оскільки в цьому випадку функції
,
називається однорідним.
Оскільки в цьому випадку функції
![]() лінійні, то будь-яка пряма або площина
(чи їх частини) в стані
лінійні, то будь-яка пряма або площина
(чи їх частини) в стані
![]() тіла перейдуть в пряму або площину (чи
їх частини) тіла в стані
тіла перейдуть в пряму або площину (чи
їх частини) тіла в стані
![]() .
.
3.2. Тензор деформації
При
неоднорідному довільному деформуванні
тіла функції
![]() будуть нелінійними. Однак, в цьому
випадку, в малому околі довільної точки
тіла деформований стан може розглядатися
як однорідний, тобто прямолінійні
матеріальні елементи в околі деякої
точки
будуть нелінійними. Однак, в цьому
випадку, в малому околі довільної точки
тіла деформований стан може розглядатися
як однорідний, тобто прямолінійні
матеріальні елементи в околі деякої
точки
![]() перетворюються в прямолінійні елементи
деформованого стану околу точки
перетворюються в прямолінійні елементи
деформованого стану околу точки
![]() .
.
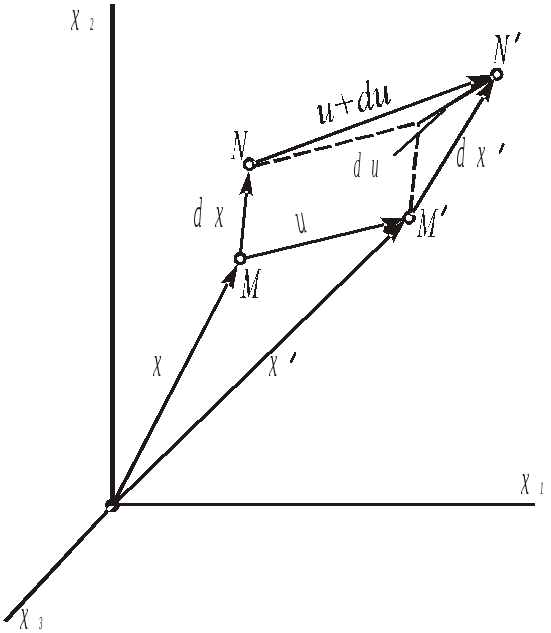
Нехай
в загальному випадку деформування тіла
дві безмежно близькі точки
![]() і
і
![]() ,
відстань між якими
,
відстань між якими
![]() в початковому стані
в початковому стані
![]() (рис. 3.2), зміщуються в положення
(рис. 3.2), зміщуються в положення
![]() і
і
![]() стану
стану
![]() .
У результаті цього лінійний елемент
.
У результаті цього лінійний елемент
![]() ,
обмежений точками
,
обмежений точками
![]() і
і
![]() ,
перетворюється в лінійний елемент
,
перетворюється в лінійний елемент
![]() ,
обмежений точками
,
обмежений точками
![]() і
і
![]() .
.
Виразимо компоненти точок деформованого стану через відповідні компоненти недеформованого стану. З умови
![]()
 (3.5)
(3.5)
визначаємо
![]() , (3.6)
, (3.6)
де
![]() – компоненти вектора зміщення точки
– компоненти вектора зміщення точки
![]() .
.
Ступінь
деформації відрізка
![]() залежить від різниці квадратів довжин
залежить від різниці квадратів довжин
![]() і
і
![]() ,
які в розглянутих координатах мають
вигляд
,
які в розглянутих координатах мають
вигляд
Рис. 3.2
![]() ; (3.7)
; (3.7)
![]() ,
,
або
![]() . (3.8)
. (3.8)
Компоненти
![]() вектора
вектора
![]() ,
визначаються за формулами
,
визначаються за формулами
![]() . (3.9)
. (3.9)
З урахуванням (3.9) вираз (3.8) можна записати у вигляді
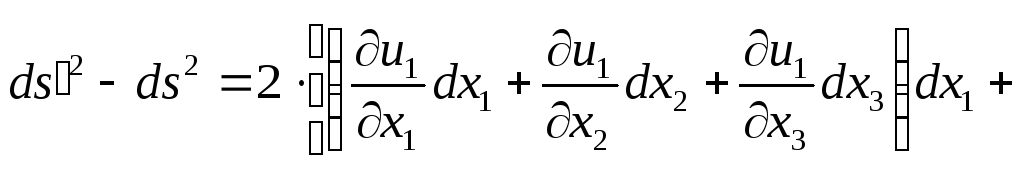
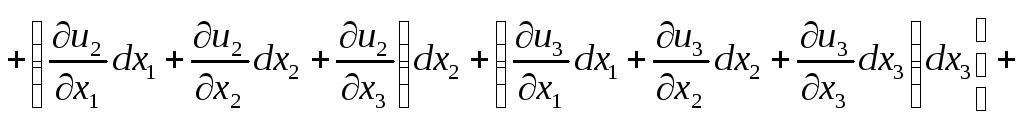
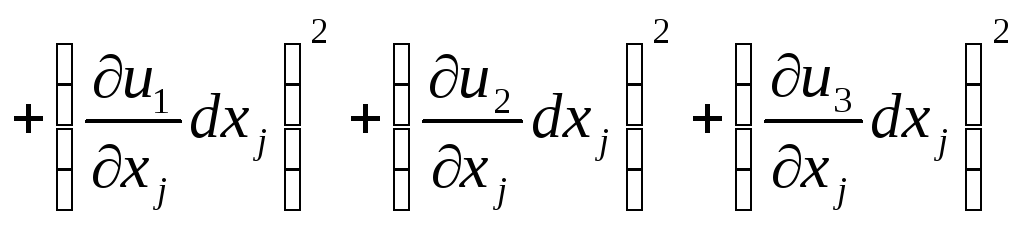 . (3.10)
. (3.10)
Оскільки
ми розглядаємо малі деформації і
відповідно малі зміщення
![]() ,
то із умов неперервності малими будуть
похідні від компонент зміщення. Це
дозволяє нехтувати квадратами або
добутками похідних у порівнянні з
похідними. Зауважимо, що це можна робити
у випадку лінійної теорії пружності. У
цьому випадку
,
то із умов неперервності малими будуть
похідні від компонент зміщення. Це
дозволяє нехтувати квадратами або
добутками похідних у порівнянні з
похідними. Зауважимо, що це можна робити
у випадку лінійної теорії пружності. У
цьому випадку
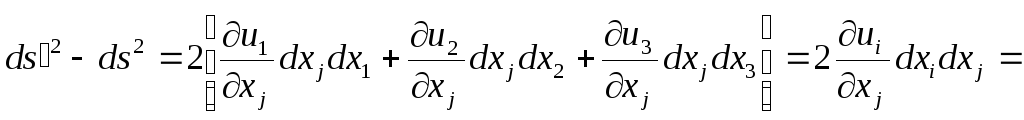
![]() (3.11)
(3.11)
Права
частина (3.11) є квадратична форма змінних
![]() ,
,
![]() ,
які визначають величину і напрям вектора
,
які визначають величину і напрям вектора
![]() .
Цю квадратичну форму можна записати у
вигляді
.
Цю квадратичну форму можна записати у
вигляді
![]() . (3.12)
. (3.12)
Її
коефіцієнти
![]() визначають симетричну матрицю третього
порядку
визначають симетричну матрицю третього
порядку
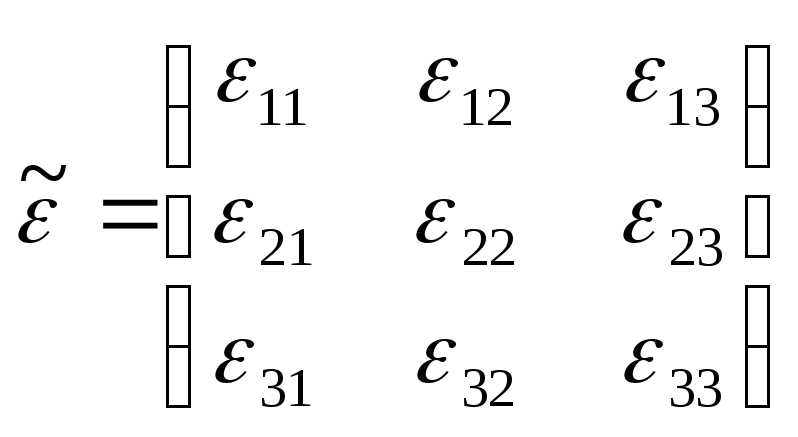 , (3.13)
, (3.13)
яка
характеризує деформований стан в точці
![]() .
.
Порівнюючи праві частини (3.11), (3.12), знаходимо
![]() ;
;
![]() ;
;
![]() ;
;
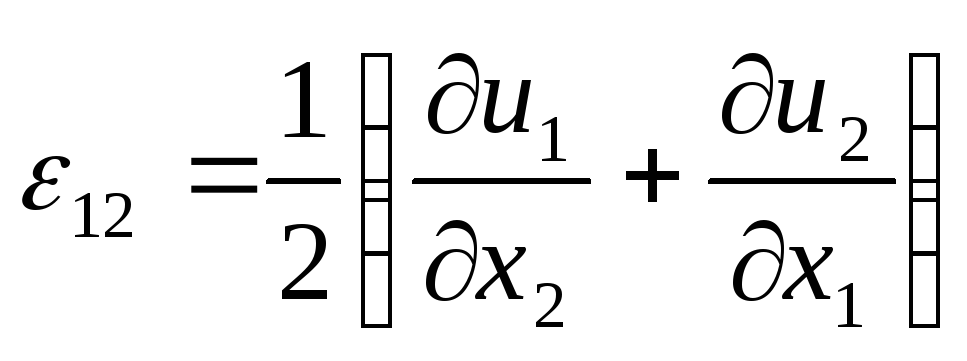 ;
;
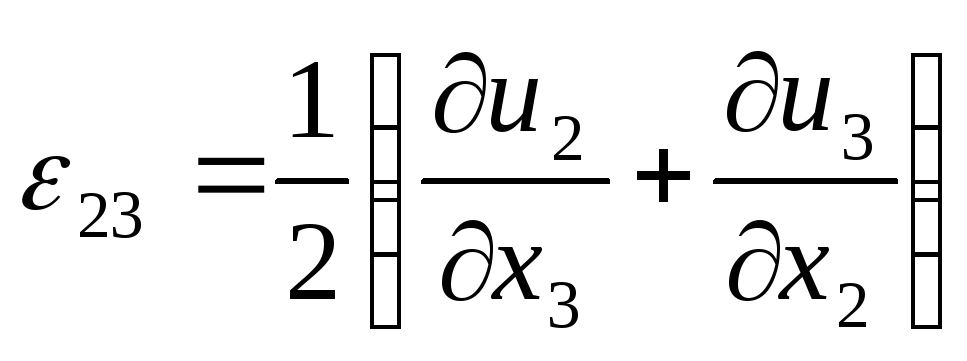 ;
;
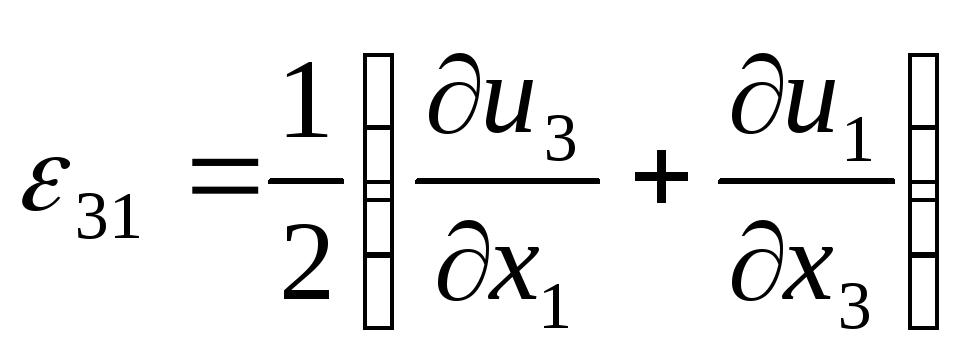 , (3.14)
, (3.14)
або в символічному вигляді
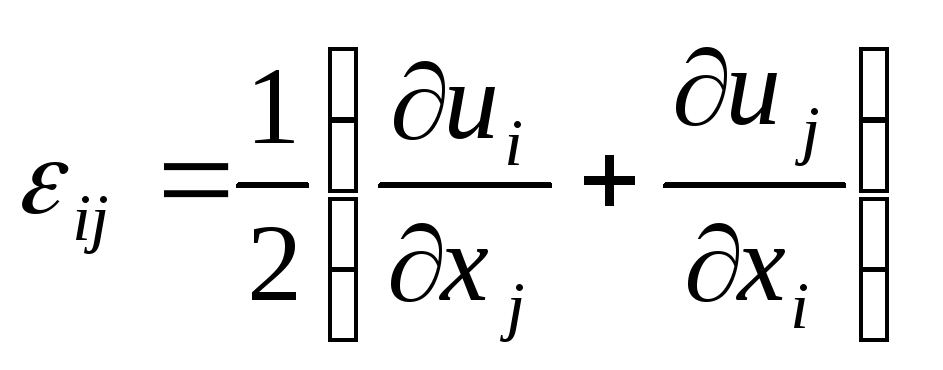
![]() . (3.15)
. (3.15)
Співвідношення
(3.14) або (3.15) називаються диференціальними
залежностями Коші.
Вони встановлюють зв’язок між компонентами
вектора зміщення точки
![]() і коефіцієнтами квадратичної форми
(3.12), які називаються компонентами
тензора деформації.
Зауважимо, що величини
і коефіцієнтами квадратичної форми
(3.12), які називаються компонентами
тензора деформації.
Зауважимо, що величини
![]() обчислюються в точці
обчислюються в точці
![]() і не залежать від вибору точки
і не залежать від вибору точки
![]() .
Ліва частина (3.11) інваріантна при
перетвореннях системи координат. Тому
на підставі відповідних теорем тензорного
аналізу вираз
.
Ліва частина (3.11) інваріантна при
перетвореннях системи координат. Тому
на підставі відповідних теорем тензорного
аналізу вираз
![]() є тензором другого рангу, який називається
тензором
малої деформації з матрицею
є тензором другого рангу, який називається
тензором
малої деформації з матрицею
![]() .
.
Вияснимо
геометричний зміст компонент тензора
![]() .
Відносне лінійне видовження лінійного
елемента
.
Відносне лінійне видовження лінійного
елемента
![]() позначимо через
позначимо через
![]() ,
тоді
,
тоді
![]() або
або
![]() . (3.16)
. (3.16)
Підставимо
(3.16) в (3.12) і поділимо на
![]()
![]() або
або
![]() , (3.17)
, (3.17)
де
![]() ;
;
![]() – косинуси кутів, які утворює елемент
– косинуси кутів, які утворює елемент
![]() з координатними осями
з координатними осями
![]() ,
,
![]() відповідно. Якщо розглядати малі
деформації (
відповідно. Якщо розглядати малі
деформації (![]() ),
то з (3.17) одержимо
),
то з (3.17) одержимо
![]() . (3.18)
. (3.18)
Нехай
лінійний елемент
![]() був паралельним координатній осі
був паралельним координатній осі
![]() .
У цьому випадку
.
У цьому випадку
![]() ,
а
,
а
![]() якщо
якщо
![]() ,
,
![]() .
Тоді з (3.18) одержимо
.
Тоді з (3.18) одержимо
![]() , (3.19)
, (3.19)
де
![]() – діагональна компонента тензора
– діагональна компонента тензора
![]() ,
тобто одна із компонент
,
тобто одна із компонент
![]() ,
,
![]() ,
,
![]() .
Таким чином, діагональні елементи
матриці тензора малої деформації
характеризують відносні лінійні
видовження в напрямках відповідних
координатних осей.
.
Таким чином, діагональні елементи
матриці тензора малої деформації
характеризують відносні лінійні
видовження в напрямках відповідних
координатних осей.
Розглянемо
тепер два лінійних елементи
![]() і
і
![]() ,
які виходять з однієї точки
,
які виходять з однієї точки
![]() і визначаються векторами
і визначаються векторами
![]() і
і
![]() .
Позначимо через
.
Позначимо через
![]() кут, який вони утворювали до деформації.
Тоді
кут, який вони утворювали до деформації.
Тоді
![]() . (3.20)
. (3.20)
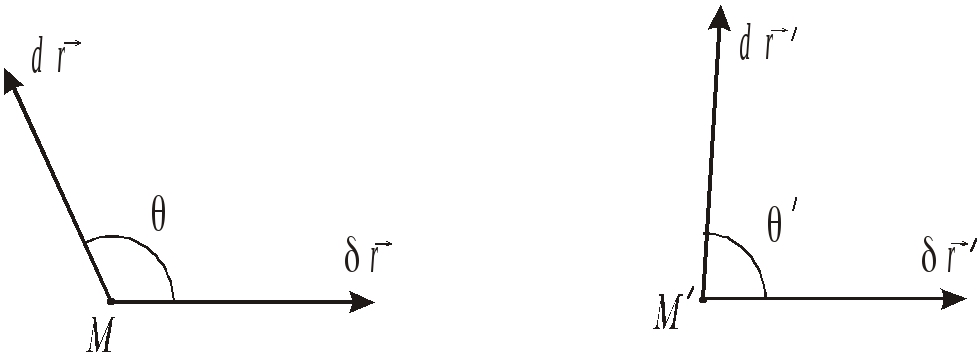
Рис. 3.3
Внаслідок
деформації елемент
![]() перейде в елемент
перейде в елемент
![]() ,
а елемент
,
а елемент
![]() в елемент
в елемент
![]() (рис. 3.3). При цьому
(рис. 3.3). При цьому
![]() ,
,
![]() .
Кут між елементами
.
Кут між елементами
![]() ,
,
![]() внаслідок деформації позначимо через
внаслідок деформації позначимо через
![]() ,
для якого
,
для якого
![]() , (3.21)
, (3.21)
де
![]() ,
,
![]() – відносне лінійне видовження елементів
– відносне лінійне видовження елементів
![]() і
і
![]() .
.
Оскільки
ми розглядаємо малі деформації, то можна
знехтувати величинамии
![]() ,
,
![]() в порівнянні з одиницею та скалярним
добутком
в порівнянні з одиницею та скалярним
добутком
![]() .
В цьому випадку формула (3.21) приймає
вигляд
.
В цьому випадку формула (3.21) приймає
вигляд
![]() . (3.22)
. (3.22)
Допустимо,
що лінійні елементи
![]() ,
,
![]() мали напрямки координатних осей
мали напрямки координатних осей
![]() ,
,
![]()
![]() відповідно, тому
відповідно, тому
![]()
![]() .
.
Обчислимо значення величин, які входять в праву частину (3.22)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; (3.23)
; (3.23)
![]() .
.
Підставляючи (3.23) в (3.22), визначаємо
![]() . (3.24)
. (3.24)
Враховуючи в (3.24) співвідношення
![]() ;
;
![]() ,
,
одержимо
при
![]()
![]()
![]()
![]()
![]() . (3.25)
. (3.25)
Позначимо
![]() ,
де
,
де
![]() – зсув прямого кута
– зсув прямого кута
![]() внаслідок деформації. Тоді
внаслідок деформації. Тоді
![]() .
.
Для
малих деформацій
![]() ,
тому
,
тому
![]() . (3.26)
. (3.26)
Недіагональні елементи тензора деформації визначають зсуви прямих кутів між відповідними координатними осями.
Враховуючи (3.26), диференціальні залежності Коші можна записати у вигляді
![]() ;
;
![]() ,
,
![]() . (3.27)
. (3.27)
