
- •Механіка суцільного середовища
- •Кінематика суцільного середовища
- •Основні поняття і задачі механіки суцільного середовища
- •Способи задання руху суцільного середовища
- •Розділ 2 елементи гідродинаміки
- •2.1. Основні поняття і формули векторного аналізу
- •2.2. Рівняння неперервності руху ідеальної рідини
- •2.3. Рівняння Ейлера
- •2.4. Гідростатика
- •2.5. Умова відсутності конвекції
- •2.6. Рівняння Бернуллі
- •Основи теорії пружності (теорія деформації)
- •3.1. Вектор зміщення і деформований стан
- •3.2. Тензор деформації
- •3.3. Перетворення компонент тензора деформації при заміні системи відліку
- •3.4. Головні напрямки тензора деформації. Головні осі і головні деформації
- •3.5. Визначення компонент вектора зміщення через компоненти тензора деформації
- •3.6. Визначення зміщень через компоненти тензора відносного зміщення
- •Основи теорії пружності (теорія напружень)
- •4.1 Зовнішні сили. Вектор напруження. Напружений стан тіла
- •4.2. Тензор напружень
- •4.3. Диференціальні рівняння рівноваги пружного тіла. Симетричність тензора напружень
- •4.4. Перетворення компонент тензора напружень при повороті системи координат
- •4.5. Головні напруження і інваріанти тензора напружень
- •Основи теорії пружності (співвідношення між компонентами тензора напружень)
- •5.1. Узагальнений закон Гука
- •Основи теорії пружності (основні рівняння і задачі теорії пружності)
- •6.1. Основні рівняння теорії пружності
- •6.2. Основні задачі статики пружного тіла
- •6.3. Пряма і обернена задачі теорії пружності
- •6.4. Рівняння пружної рівноваги в зміщеннях
- •6.5. Основні рівняння в напруженнях
- •Застосовуючи до (6.32) оператор Лапласа, одержимо
- •6.6. Напівобернений метод Сен-Венана
- •6.7. Принцип Сен-Венана
- •Найпростіші задачі теорії пружності
- •Метод суперпозиції
- •Основи теорії пружності (плоска задача теорії пружності)
- •7.1. Плоска деформація
- •7.2. Плоский напружений стан
- •7.3. Узагальнений плоский напружений стан
- •7.4. Основні рівняння плоскої теорії пружності. Зведення до бігармонічної проблеми
- •7.5. Плоска задача в декартових координатах
- •Нехай функція напружень має вигляд полінома третього степеня
- •Виберемо функцію напружень у вигляді полінома четвертого степеня
- •Якщо розглядається друга гранична задача, то граничні умови мають вигляд
- •8.2. Зведення основної задачі до бігармонічної проблеми
- •8.3. Задачі, в яких напруження залежать тільки від
- •Задачі, в яких напруження залежать від і
- •Підставляючи (8.67) у (8.64), одержимо формули для напружень
- •Застосування функцій комплексної змінної до розв’язування задач плоскої теорії пружності
- •9.1. Комплексне подання функції напружень
- •Розглянемо основне рівняння плоскої теорії пружності
- •9.2. Комплексне подання компонент тензора напружень і вектора зміщень
- •9.3. Степінь визначеності і структура комплексних потенціалів
- •9.4. Перетворення рівнянь плоскої задачі теорії пружності при конформному відображенні
- •9.5. Двосторонній розтяг нескінченної площини з еліптичним отвором
- •Список літератури
9.3. Степінь визначеності і структура комплексних потенціалів
За
першою із формул (9.32) сума напружень
визначається тільки дійсною частиною
функції
![]() ,
тому до її уявної частини можна додати
сталу
,
тому до її уявної частини можна додати
сталу
![]() .
Звідси випливає, що при заданих напруженнях
функція
.
Звідси випливає, що при заданих напруженнях
функція
![]() визначається з точністю до доданка
визначається з точністю до доданка
![]() ,
а функція
,
а функція
![]() ,
відповідно, – з точністю до
,
відповідно, – з точністю до
![]() (
(![]() ,
,
![]() – дійсні сталі).
– дійсні сталі).
Формула
(9.33) показує, що при заданому тензорі
напружень функція
![]() визначається однозначно, а функція
визначається однозначно, а функція
![]() – з точністю до сталої
– з точністю до сталої
![]() .
.
Таким чином, при заміні
![]() на
на
![]() ;
;
![]() на
на
![]() (9.39)
(9.39)
напруження не зміняться, а комплексна комбінація зміщень (9.30) одержить приріст
![]() , (9.40)
, (9.40)
який виражає собою, як і слід було очікувати, жорстке зміщення тіла.
Із
(9.40) випливає, що при заданих зміщеннях
сталі
![]() ,
,
![]() i
i
![]() повинні задовольняти умовам
повинні задовольняти умовам
![]() ;
;
![]() . (9.41)
. (9.41)
Якщо
система координат вибрана так, що її
початок знаходиться в області
![]() ,
зайнятій тілом, то довільні сталі
,
зайнятій тілом, то довільні сталі
![]() ,
,
![]() ,
,
![]() можна відповідним чином зафіксувати.
Наприклад, при заданих напруженнях,
коли всі сталі є довільними, систему
координат можна вибрати так, що
можна відповідним чином зафіксувати.
Наприклад, при заданих напруженнях,
коли всі сталі є довільними, систему
координат можна вибрати так, що
![]() ;
;
![]() ;
;
![]() . (9.42)
. (9.42)
Якщо
задано зміщення, тоді довільно можна
вибирати
![]() або
або
![]() .
В такому разі можна вважати, що
.
В такому разі можна вважати, що
![]() або
або
![]() . (9.43)
. (9.43)
Компоненти
тензора напружень і компоненти зміщень,
як відомо, – однозначні функції
розглядуваної точки тіла. Тому й
комплексні потенціали повинні бути
також однозначними функціями. Проте
аналітичні функції
![]() і
і
![]() можуть бути й багатозначними. Значною
мірою це залежить від типу області, яку
займає розглядуване тіло. Якщо область
однозв’язна, то очевидно, ці функції
будуть однозначними.
можуть бути й багатозначними. Значною
мірою це залежить від типу області, яку
займає розглядуване тіло. Якщо область
однозв’язна, то очевидно, ці функції
будуть однозначними.
Розглянемо
випадок, коли тіло займає неоднозв’язну
область
![]() із зовнішнім контуром
із зовнішнім контуром
![]() і внутрішніми контуруми
і внутрішніми контуруми
![]() (
(![]() ).
Перша з формул (9.32) показує, що дійсна
частина функції
).
Перша з формул (9.32) показує, що дійсна
частина функції
![]() є однозначною для будь-якої області.
Отже, при обході вздовж будь-якого
контуру
є однозначною для будь-якої області.
Отже, при обході вздовж будь-якого
контуру
![]() ,
що охоплює контур
,
що охоплює контур
![]() ,
дійсна частина
,
дійсна частина
![]() приросту не одержить, а уявна частина
одержить приріст
приросту не одержить, а уявна частина
одержить приріст
![]() ,
де
,
де
![]() – дійсна стала. При такій зміні функції
– дійсна стала. При такій зміні функції
![]() напружений стан залишається незмінним.
Для зручності сталу
напружений стан залишається незмінним.
Для зручності сталу
![]() будемо записувати так:
будемо записувати так:
![]() .
.
Розглянемо тепер функцію
![]() , (9.44)
, (9.44)
де
![]() – довільно вибрані точки в середині
контурів
– довільно вибрані точки в середині
контурів
![]() .
.
Оскільки
функція
![]() при обході контуру
при обході контуру
![]() одержує приріст
одержує приріст
![]() ,
вираз
,
вираз
![]() одержує точно такий приріст, який може
мати функція
одержує точно такий приріст, який може
мати функція
![]() при обході контуру
при обході контуру
![]() .
Інші доданки суми (9.44) приросту не
одержують. Таким чином, функція
.
Інші доданки суми (9.44) приросту не
одержують. Таким чином, функція
![]() буде вже однозначною. Тому комплексний
потенціал в загальному випадку
багатозв’язної області можна записати
так
буде вже однозначною. Тому комплексний
потенціал в загальному випадку
багатозв’язної області можна записати
так
![]() , (9.45)
, (9.45)
де
![]() – голоморфна (однозначна) функція в
розглядуваній області,
– голоморфна (однозначна) функція в
розглядуваній області,
![]() – дійсні сталі.
– дійсні сталі.
Далі,
інтегруючи (9.45), для функції
![]() одержимо
одержимо
![]()
![]() голоморфна
функція. (9.46)
голоморфна
функція. (9.46)
Тут враховано, що інтеграл від однозначної функції може бути неоднозначною функцією.
Перегрупувавши доданки у формулі (9.46), одержимо
![]() . (9.47)
. (9.47)
Тут
![]() – комплексна стала,
– комплексна стала,
![]() – голоморфна функція в розглядуваній
області
– голоморфна функція в розглядуваній
області
![]() .
.
Розглянемо
формулу (9.33), з якої випливає, що функція
![]() голоморфна в області
голоморфна в області
![]() .
Для функції
.
Для функції
![]() ,
аналогічно до попереднього одержимо
,
аналогічно до попереднього одержимо
![]() , (9.48)
, (9.48)
де
![]() – голоморфна функція в області
– голоморфна функція в області
![]() ,
,
![]() – комплексна стала.
– комплексна стала.
Встановимо
тепер, яким умовам повинні задовольняти
сталі
![]() ,
,
![]() ,
,
![]() для того, щоб компоненти вектора зміщення
були однозначними функціями. Підставляючи
(9.47), (9.48) в формулу (9.30), одержимо
для того, щоб компоненти вектора зміщення
були однозначними функціями. Підставляючи
(9.47), (9.48) в формулу (9.30), одержимо
![]()
або
![]() ,
,
![]() (
(![]() ). (9.49)
). (9.49)
Покажемо,
що величини
![]() і
і
![]() можна виразити через компоненти
можна виразити через компоненти
![]() головного вектора зовнішніх зусиль,
прикладених до контуру
головного вектора зовнішніх зусиль,
прикладених до контуру
![]() з боку зовнішньої нормалі
з боку зовнішньої нормалі
![]() по відношенню до області
по відношенню до області
![]() .
Для цього обчислимо головний вектор
зовнішніх зусиль, прикладених до контуру
.
Для цього обчислимо головний вектор
зовнішніх зусиль, прикладених до контуру
![]() .
Нехай
.
Нехай
![]() ,
,
![]() – компоненти зусиль до контуру
– компоненти зусиль до контуру
![]() .
На підставі формул (9.29), (9.36) можемо
записати
.
На підставі формул (9.29), (9.36) можемо
записати
![]() . (9.50)
. (9.50)
Виходячи з формул (9.47), (9.48) і (9.50), знаходимо
![]() . (9.51)
. (9.51)
На підставі формул (9.49), (9.51) одержимо
![]() ;
;
![]() ;
;
![]() . (9.52)
. (9.52)
Підставляючи (9.52) в (9.47), (9.48), запишемо вирази для комплексних потенціалів
![]() ;
;
![]() , (9.53)
, (9.53)
де
![]() ,
,
![]() – голоморфні функції в розглядуваній
області
– голоморфні функції в розглядуваній
області
![]() .
.
Розглянемо
окремо випадок, коли область
![]() є нескінченною пластиною з отворами. В
такому разі розглядувана область є
граничним випадком області, обмеженої
контурами
є нескінченною пластиною з отворами. В
такому разі розглядувана область є
граничним випадком області, обмеженої
контурами
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
коли контур
,
коли контур
![]() віддалений “на нескінченність”.
віддалений “на нескінченність”.
Встановимо
структуру комплексних потенціалів в
околі нескінченно віддаленої точки
області
![]() .
Для довільної точки зовні контури
.
Для довільної точки зовні контури
![]() ,
який охоплює всі інші контури
,
який охоплює всі інші контури
![]() ,
маємо
,
маємо
![]() ,
тому
,
тому
![]() (9.54)
(9.54)
при
![]() .
.
Тоді формули (9.53) для нескінченної багатозв’язної області можна записати у вигляді
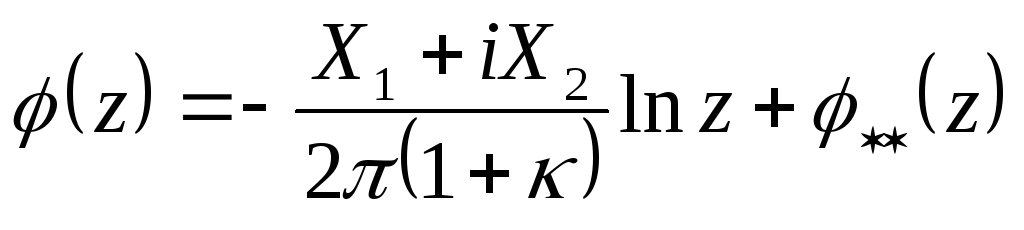 ;
;
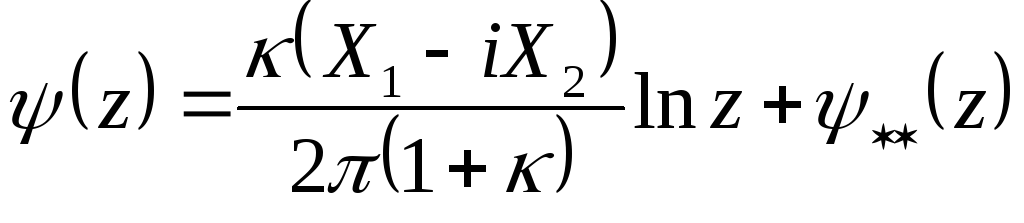 . (9.55)
. (9.55)
Тут
![]() ;
;
![]() – компоненти головного вектора зовнішніх
зусиль;
– компоненти головного вектора зовнішніх
зусиль;
![]() ,
,
![]() – голоморфні функції в області
– голоморфні функції в області
![]() за винятком нескінченно віддаленої
точки, де ці функції можуть мати полюси
скінченого порядку. Ці функції в околі
нескінченно віддаленої точки подамо
так
за винятком нескінченно віддаленої
точки, де ці функції можуть мати полюси
скінченого порядку. Ці функції в околі
нескінченно віддаленої точки подамо
так
![]() ;
;
![]() , (9.56)
, (9.56)
де
![]() ,
,
![]() – комплексні сталі, які визначаються
із умов напруженого стану при
– комплексні сталі, які визначаються
із умов напруженого стану при
![]() ;
;
![]() ,
,
![]() – голоморфні функції у всій площині
– голоморфні функції у всій площині
![]() .
.
Допустимо,
що компоненти тензора напружень обмежені
в усій розглядуваній області
![]() ,
включаючи нескінченно віддалену точку.
Позначимо через
,
включаючи нескінченно віддалену точку.
Позначимо через
![]() ,
,
![]() ,
,
![]() компоненти тензора напружень при
компоненти тензора напружень при
![]() .
.
Підставляючи
(9.56) у формули (9.32), (9.33) при
![]() ,
знаходимо
,
знаходимо
![]() ;
;
![]()
або
![]() ;
;
![]() . (9.57)
. (9.57)
Решта
коефіцієнтів
![]() ,
,
![]() дорівнюють нулю.
дорівнюють нулю.
Таким чином, для необмеженої пластинки з одним отвором, коли “на нескінченності” задано однорідне поле напружень, комплексні потенціали мають таку структуру
![]() ;
;
![]() . (9.58)
. (9.58)
Тут
![]() ,
,
![]() – голоморфні в розглядуваній області
функції,
– голоморфні в розглядуваній області
функції,
![]() ,
,
![]() – компоненти головного вектора зовнішніх
сил, прикладених до контуру отвору;
– компоненти головного вектора зовнішніх
сил, прикладених до контуру отвору;
![]() ,
,
![]() – сталі, що визначаються за формулами
(9.57).
– сталі, що визначаються за формулами
(9.57).
