3. Задачі, в яких напруження залежать від і

Серед таких задач є задачі для кругового кільця або його частини, в яких напруження пропорційні або , тобто є функціями вигляду або . Такому розподілу напружень відповідає бігармонічна функція

, (8.56)

де , – функції тільки ; , – сталі.

Розглянемо частковий випадок задачі (; ) і підставимо (8.56) у (8.28). Для визначення одержимо таке рівняння

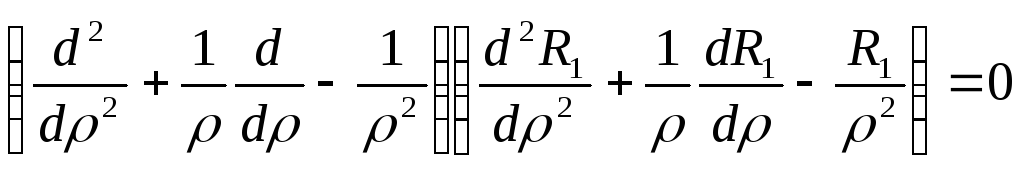
або

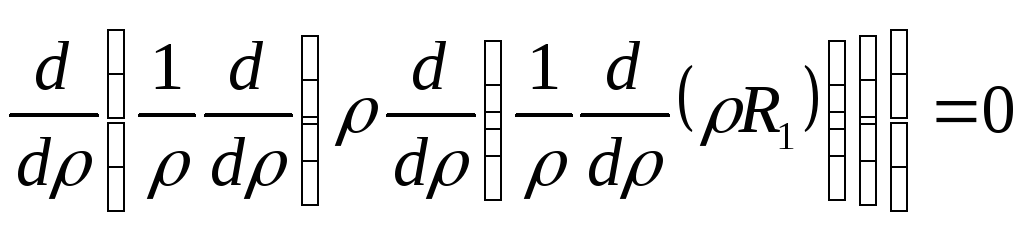. (8.57)

Після чотирикратного інтегрування (8.57) по , знаходимо

. (8.58)

Тоді функцію напружень (8.56) запишемо у вигляді

. (8.59)

За формулами (8.27) визначаємо компоненти тензора напружень

;

; (8.60)

.

Оскільки – лінійний вираз, тому постійна у формули (8.60) не входить.

Компоненти тензора деформації у випадку плоского напруженого стану на підставі (8.22), (8.26) визначаються співвідношеннями

;

;

. (8.61)

Для визначення компонент вектора зміщення необхідно проінтегрувати рівняння (8.61).

Якщо розглянути інший частковий випадок функції , коли , , то одержимо залежності, аналогічні до (8.58)-(8.61). Об’єднуючи ці два часткові випадки, функцію напружень подамо у вигляді

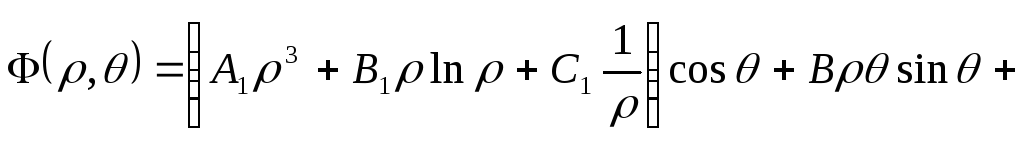
. (8.62)

8.4.1. Згин кривого стержня прямокутного перерізу силою, прикладеного до незакріпленого кінця (задача Х.С. Головіна). Розглянемо кривий стержень з круговою віссю радіусом один з торців якого жорстко закріплений, а до іншого прикладена сила , що діє перпендикулярно до осі стержня (рис. 8.9).

При такому навантаженні стержня в довільному його поперечному перерізі, який визначається кутом , згинаючий момент пропорційний . Природно допустити, що в цьому випадку напруження , а отже і функція також будуть пропорційними .

Приймаючи функцію напружень у вигляді

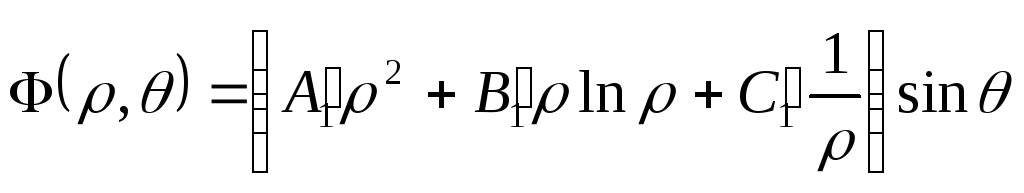, (8.63)

за формулами (8.27) знаходимо

; ;

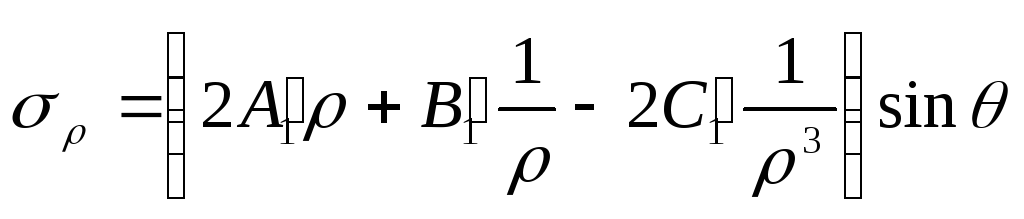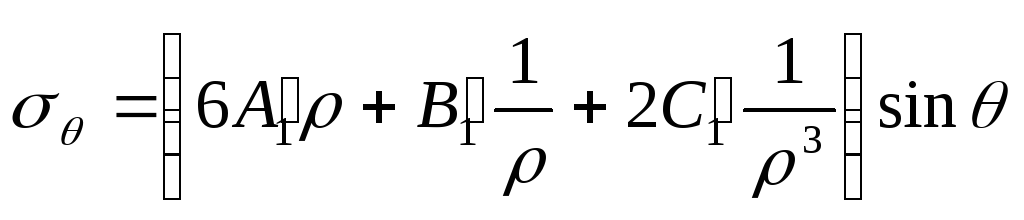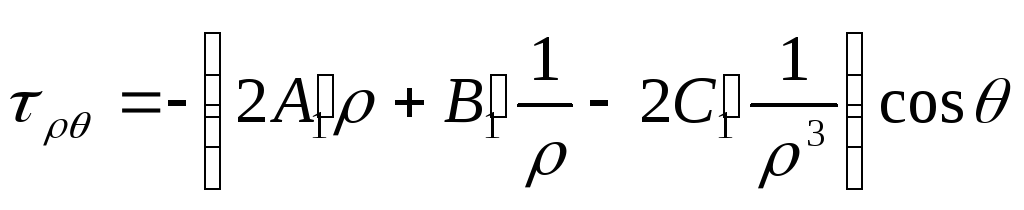. (8.64)

Граничні умови задачі мають вигляд

; ; . (8.65)

Підставляючи (8.64) в умови (8.65), запишемо систему рівнянь для визначення сталих , ,

; ;

, (8.66)

з якої знаходимо

; ; , (8.67)

де .

Підставляючи (8.67) у (8.64), одержимо формули для напружень

; ;

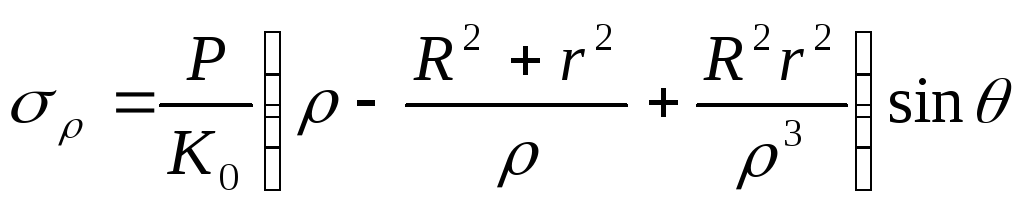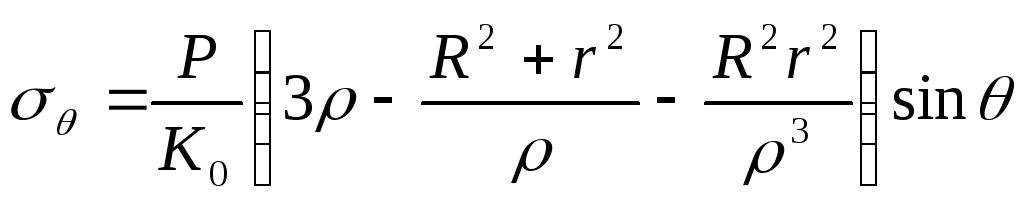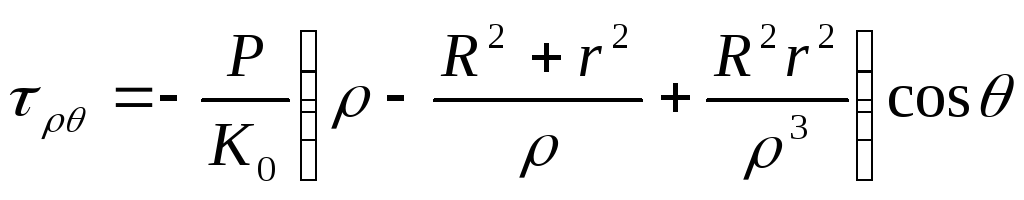. (8.68)

Р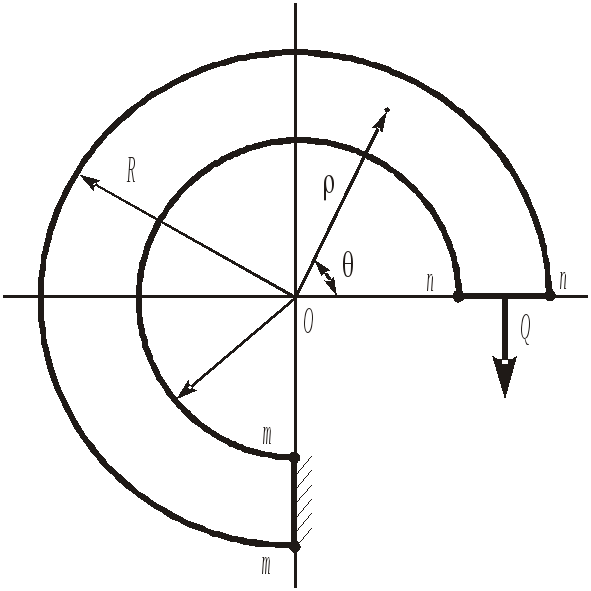озглянемо тепер навантаження стержня силою , яка діє перпендикулярно до вільного торця (рис. 8.10 а). У цьому випадку згинаючий момент пропорційний . Приймаючи

, (8.69)

за формулами (8.27) знаходимо

Рис. 8.10 а

; ;

. (8.70)

З граничних умов задачі

; ; (8.71)

визначаємо

; ; . (8.72)

Підставляючи (8.72) в (8.70), одержимо

; ;

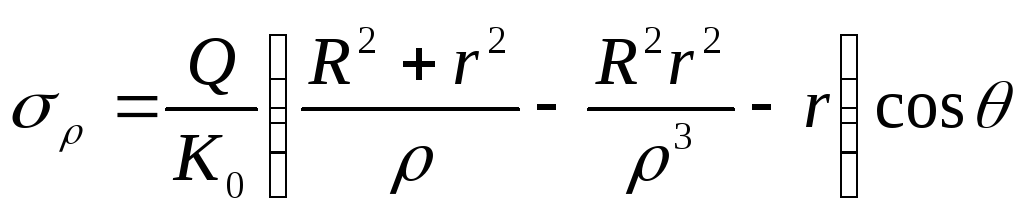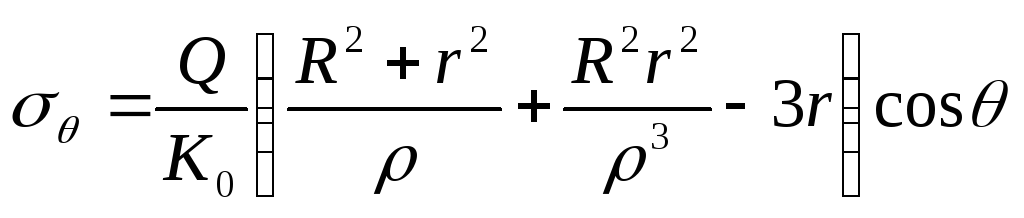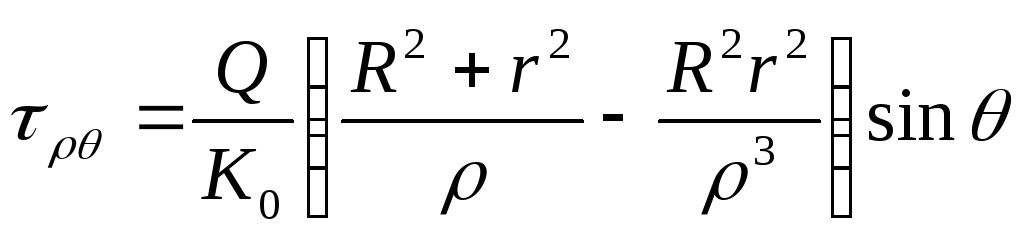, (8.73)

де стала визначається за формулами (8.67).

З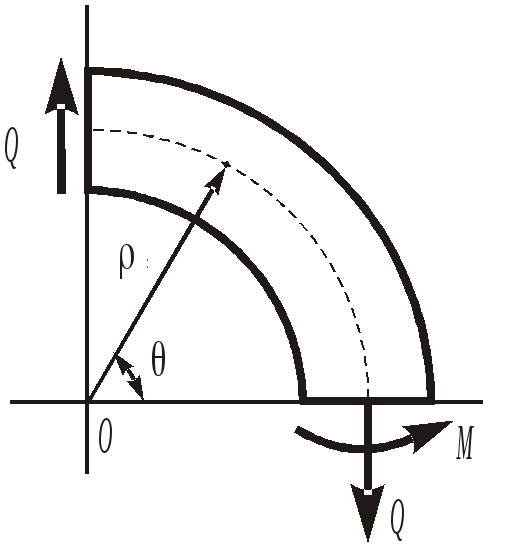 (8.67) випливає, що функція (8.69) визначає відмінний від (8.71) напружений стан, при якому в перерізі мають місце тільки дотичні напруження , які зводяться до поперечної сили 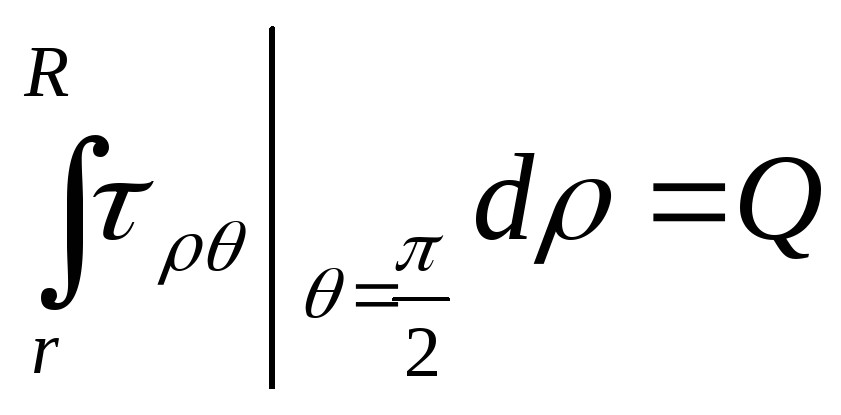, а на вільному торці розподілені сили зводяться до сили , яка прикладена в центрі торця, і пари сил з моментом (рис. 8.10 б).

П

Рис. 8.10 б

рикладаючи до вільного торця стержня момент протилежного напрямку, і враховуючи (8.55), на підставі принципу суперпозиції одержимо розв’язок поставленої задачі

;

;

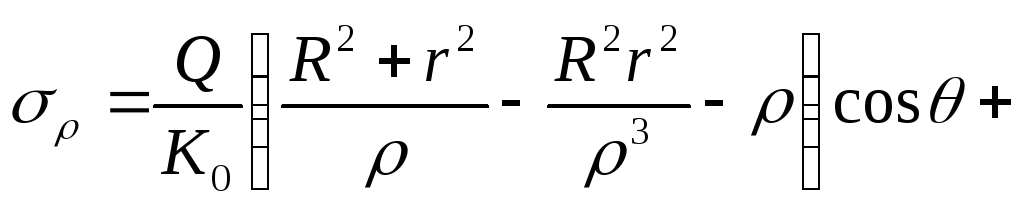
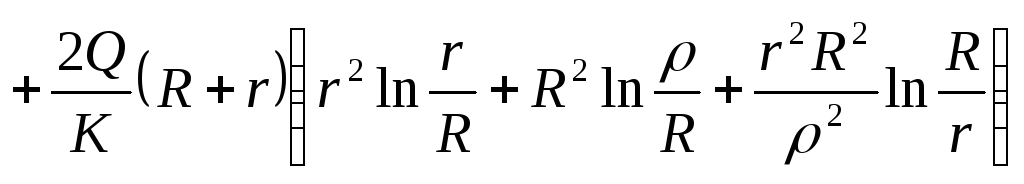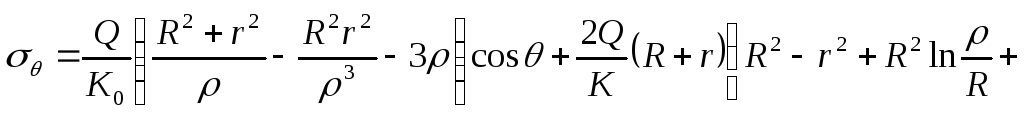
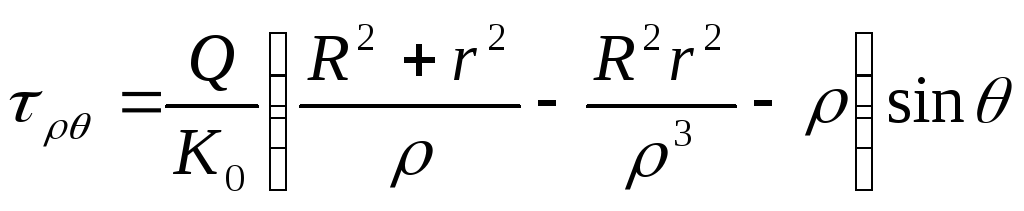. (8.74)

Маючи розв’язки (8.68) і (8.74), на підставі принципу суперпозиції можна одержати розв’язок задачі про згин розглядуваного стержня силою, довільно напрямленою в його площині і прикладеною до центра вільного торця.

8.4.2. Двосторонній розтяг нескінченої пластинки з круговим отвором. Р

Рис. 8.11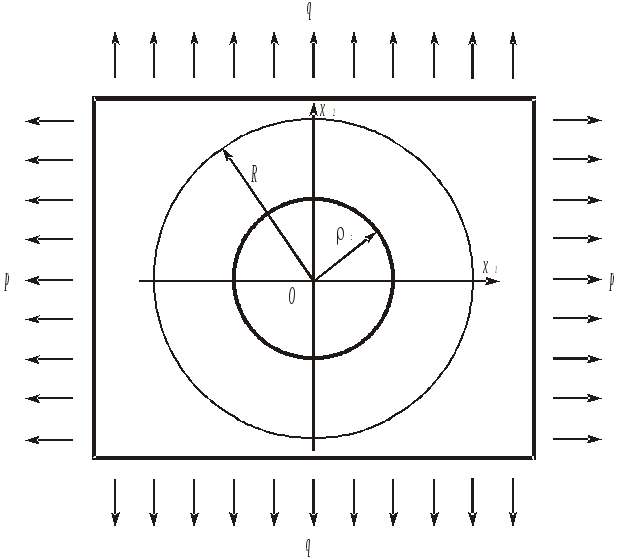

озглянемо нескінченну ізотропну площину з круговим отвором радіусом , яка перебуває в умовах двостороннього розтягу (стиску) взаємно перпендикулярними і рівномірно розподіленими напруженнями і , прикладеними “на нескінченності”. Зовнішнє навантаження на контурі отвору відсутнє. Систему прямокутних координат виберемо так, як показано на рис. 8.11. Розв’язок задачі полягає у визначенні компонент тензора напружень в кожній точці площини, зокрема, на контурі отвору.

Поряд з прямокутною виберемо полярну систему координат з полюсом в центрі отвору.

Розглянемо коло великого радіуса з центром в точці . Визначимо на цьому колі значення компонент тензора напружень у полярній системі координат. За формулами (8.8) знаходимо

;

. (8.75)

Співвідношення (8.75) показують, що у даному випадку функцію напружень можна вибрати у вигляді

, (8.76)

де – розв’язок (8.34) рівняння (8.32), – функція змінної .

Підставляючи (8.76) у (8.28), приходимо до рівняння для визначення

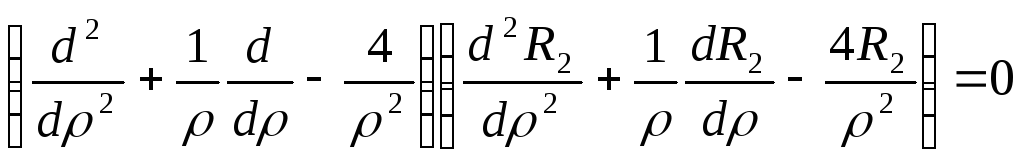, (8.77)

інтегруючи яке, знаходимо

. (8.78)

Враховуючи (8.34), (8.78), функцію напружень (8.76) запишемо так

. (8.79)

Підставляючи (8.79) у (8.27), одержимо вирази для компонент тензора напружень

;

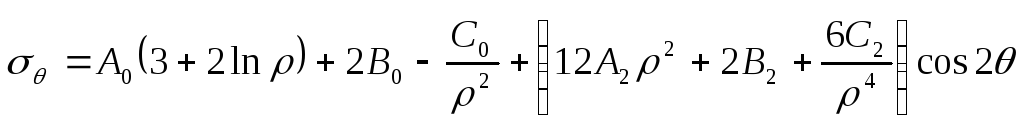; (8.80)

.

Граничні умови задачі мають вигляд

при ;

; при . (8.81)

Якщо підставити (8.80) в умови (8.81), то одержимо систему рівнянь для визначення сталих , , , , , , ,

;

;

;

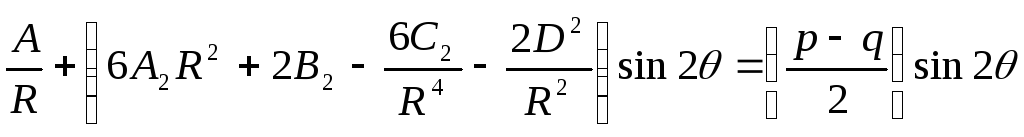. (8.82)

Ліві частини умов (8.82) при повинні приймати скінчені значення. Це можливо лише тоді, коли . У цьому випадку система (8.82) перетвориться до вигляду

; ; ;

; ; . (8.83)

Розв’язуючи (8.83), знаходимо

; ; ;

; ; . (8.84)

Враховуючи (8.84), формули (8.80) запишемо у такому вигляді

;

;

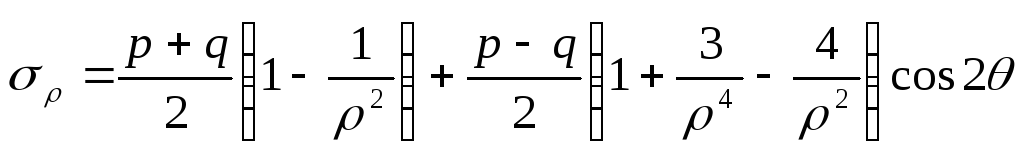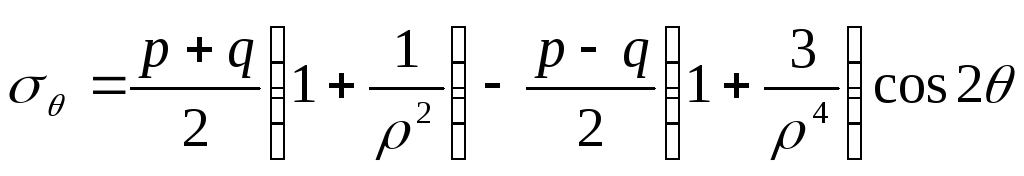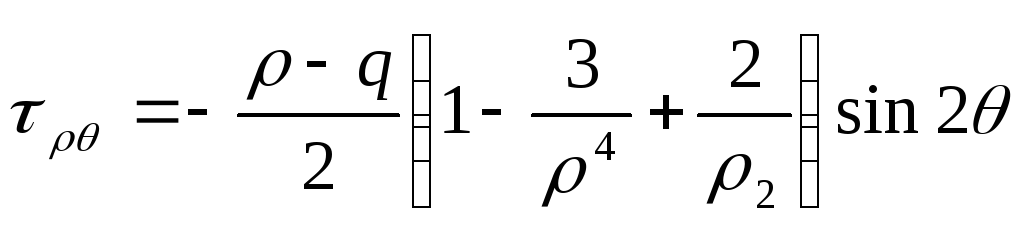. (8.85)

Якщо в (8.85) покласти , то одержимо вирази для напружень на контурі отвору

; . (8.86)

Аналізуючи формули (8.85), приходимо до висновку, що напружений стан площини із збільшенням співпадає з напруженим станом суцільної пластинки, який визначається за формулами (8.75). Це означає, що вплив отвору в нескінченній пластинці має локальний характер і швидко згасає з ростом .

РОЗДІЛ 9