Нехай функція напружень має вигляд полінома третього степеня

, (7.39)

який також є розв’язком (7.32) при довільних коефіцієнтах. У цьому випадку за формулами (7.30) визначаємо

; ; . (7.40)

Розглянемо поліном (7.39) при деяких часткових значеннях коефіцієнтів. Допустимо, що всі коефіцієнти, крім , дорівнюють нулю. Тоді

; . (7.41)

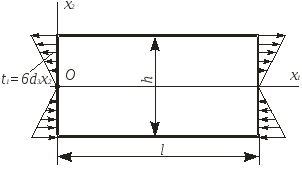
У цьому випадку функція відповідає чистому згину пластини (рис. 7.5).

На рис. 7.6 показано навантаження пластини, яке відповідає функції . Тоді маємо

; ; . (7.42)

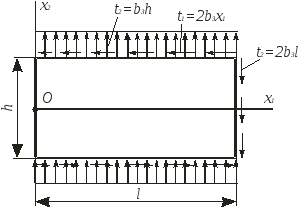
Рис. 7.5 Рис. 7.6

Виберемо функцію напружень у вигляді полінома четвертого степеня

. (7.43)

Підставивши (7.43) в (7.32), переконуємося, що це рівняння виконується якщо

, (7.44)

т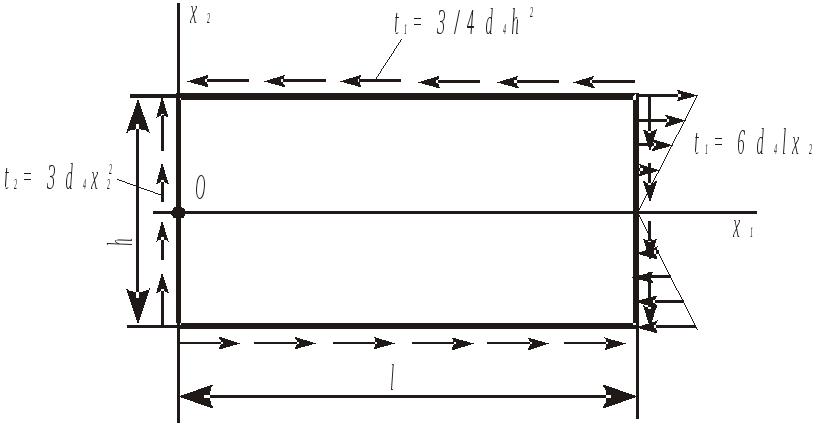обто в (7.43) довільно можна вибирати тільки чотири коефіцієнти , , і . Надаючи їм різні значення, одержимо відповідні навантаження на сторонах

п

Рис 7.7

рямокутної пластини. Покладаючи, наприклад, , , тобто за формулами (7.30) знаходимо

;. (7.45)

У

Рис. 7.7

відповідності з граничними умовами (7.35), (7.36) напруження (7.45) реалізуються при такому її навантаженні (рис. 7.7). На поздовжніх сторонах діють рівномірно розподілені дотичні напруження ; на сторонах і розподілені за параболічним законом дотичні зусилля і крім цього, на стороні діють нормальні зусилля , які змінюються за лінійним законом.

При іншому виборі незалежних коефіцієнтів розглянутих поліномів одержимо інші випадки навантаження пластини. Лінійно комбінуючи ці елементарні розв’язки, одержимо нові розв’язки, які мають практичне значення.

РОЗДІЛ 8

ОСНОВИ ТЕОРІЇ ПРУЖНОСТІ

(ПЛОСКА ТЕОРІЯ ПРУЖНОСТІ В ПОЛЯРНИХ КООРДИНАТАХ)

Якщо пружне деформівне тіло займає плоску область, яка обмежена прямими і дугами кола, то в цьому випадку при розв’язуванні задач зручно користуватися полярною системою координат.

8.1. Основні рівняння плоскої теорії пружності

в полярних координатах

Розглянемо поряд з прямокутною декартовою системою координат полярну систему координат полюс якої співпадає з точкою , а полярна вісь – з координатною віссю .

Зв’язок між декартовими і полярними координатами точки визначається залежностями

; ; (8.1)

або

; . (8.2)

Позначимо через , , компоненти тензора напружень в полярній системі координат, а через , – компоненти вектора зміщення у вибраній точці тіла. Їх додатні напрямки показано на рис. 8.1, 8.2. Із рис. 8.2 видно, що компоненти вектора зміщення в декартовій і полярній системах координат зв’язані залежностями

; (8.3)

або

; , (8.4)

де .

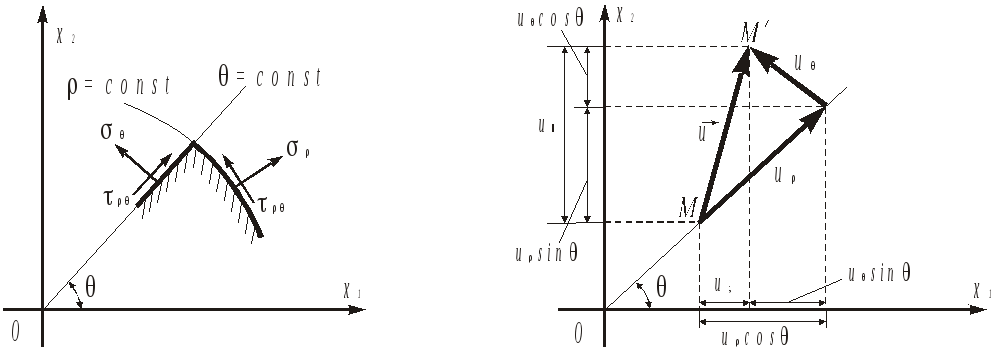
Рис. 8.1 Рис. 8.2

Д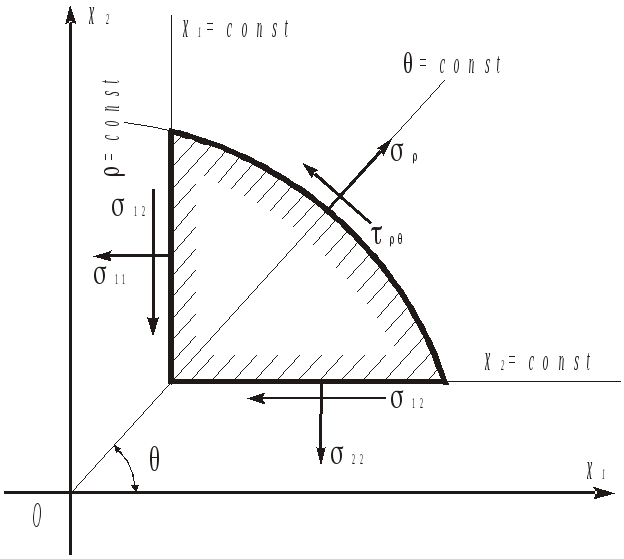ля встановлення зв’язку між компонентами тензора напружень розглянемо елемент, виділений координатними лініями , ,

(рис. 8.3).

З

Рис. 8.3

апишемо умови рівноваги збіжної системи сил, що діють на цей елемент у проекціях на напрямки і

;

. (8.5)

Тут – довжина криволінійного перерізу, , – довжини перерізів, паралельних осям , відповідно. Враховуючи, що , , із (8.5) знаходимо

;

. (8.6)

Формулу для визначення одержимо із першої рівності (8.6) заміною на

. (8.7)

На підставі (8.6), (8.7) формули переходу від компонент , , до компонент , , запишуться у вигляді

;

;

. (8.8)

Якщо (8.8) розв’язати відносно , , , то одержимо формули оберненого переходу

;

;

Рис. 8.4

. (8.9)

Додаючи два перші співвідношення (8.8) або (8.9), знаходимо

. (8.10)

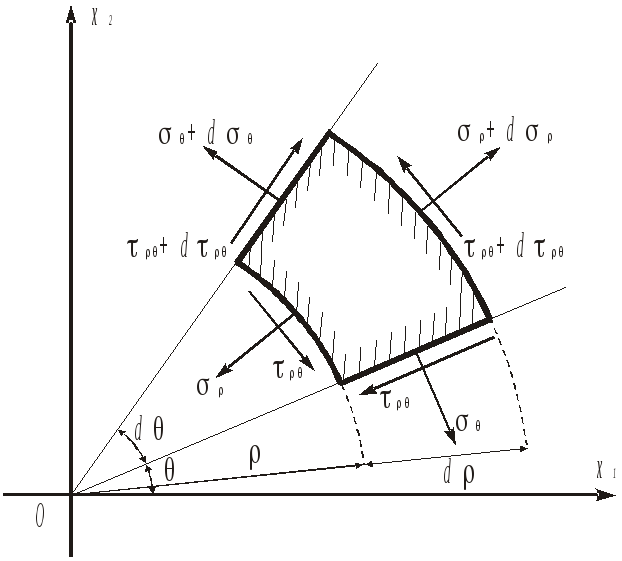
Для встановлення диференціальних рівнянь рівноваги в полярних координатах розглянемо елемент, який виділений двома парами координатних ліній (рис. 8.4).

Під дією збіжної системи сил, зображених на рис. 8.4, даний елемент повинен перебувати у рівновазі. Записуючи умови рівноваги в проекціях на напрямки і , одержимо при відсутності масових сил

;

. (8.11)

Враховуючи в (8.11), що , , і нехтуючи величинами третього порядку малості, знаходимо після ділення на диференціальні рівняння рівноваги

; . (8.12)

Граничні умови на підставі (7.28) запишуться у вигляді

; при ;

; при , (8.13)

де , – нормальні складові контурного навантаження; – дотична складова.