Кінематика суцільного середовища

1. Основні поняття і задачі механіки суцільного середовища

Механіка суцільного середовища – це розділ механіки, присвячений вивченню руху газоподібних, рідких і твердих деформівних тіл.

У теоретичній механіці вивчаються рухи матеріальної точки, дискретних систем матеріальних точок і абсолютно твердого тіла. У механіці суцільного середовища за допомогою і на основі методів, розвинутих в теоретичній механіці, розглядаються рухи неперервно суцільних матеріальних тіл, відстані між точками, які під час руху змінюються.

Крім звичайних матеріальних тіл (вода, повітря, метали) в механіці суцільного середовища розглядаються також особливі середовища – поля (електромагнітне, поле випромінювання, гравітаційне, тощо).

Можна навести приклади різноманітних рухів рідин, газів і твердих деформівних тіл, з якими ми зустрічаємося при вивченні явищ природи і розв’язуванні конкретних технічних задач. Багатьма рухами деформівних тіл ми можемо керувати в необхідній мірі, спираючись на повсякденний елементарний власний досвід. Однак, в окремих випадках потрібні спеціальні методи теоретичних і експериментальних досліджень. Проведення подібних досліджень привело до створення і розвитку механіки суцільного середовища як науки.

Відзначимо, що існує багато питань і проблем, на які наука ще не може дати необхідної задовільної відповіді за допомогою відомих експериментальних і теоретичних методів. Вирішення нових складних проблем, які мають наукове та прикладне значення, і задач, дослідження яких зумовлено попереднім розвитком науки, є на теперішній час предметом науково-дослідної роботи.

Розглянемо окремі, найбільш важливі проблеми механіки суцільного середовища.

Проблема взаємодії рідини і газу на рухомі в них тіла. Сили, які діють з боку рідини на тіло, визначаються рухом рідини, тому вивчення руху тіл у рідині безпосередньо пов’язано з вивченням руху рідини. Особливим стимулом для вирішення цієї проблеми стали технічні задачі про рух літаків, снарядів, ракет, кораблів, підводних човнів, задачі створення різноманітних рушійних пристроїв – водяних і повітряних гвинтів.

Рух рідини і газу по трубопроводах. Для таких задач основне значення мають закони взаємодії рідини з границями потоку і, зокрема, величина опору рухомих та нерухомих твердих стінок, явища нерівномірності розподілу швидкостей і т.п. Ці задачі мають безпосереднє практичне значення при проектуванні газопроводів, нафтопроводів, водопроводів, насосів, турбін і інших гідравлічних машин.

Фільтрація – рух рідини через ґрунт та інші пористі середовища. У ґрунті постійно відбувається рух води, який необхідно врахувати при побудові фундаментів різних споруд (плотин, опор мостів, гідростанцій), при створенні підземних тунелів. Велике значення фільтрація має в нафтовій та газовидобувній справі.

Хвильові рухи. Розповсюдження хвиль в твердих тілах; хвилі на поверхні морів і океанів; хвилі, викликані рухом корабля; припливи і відпливи; сейсмічні процеси; звукові коливання; загальна проблема шуму в різних середовищах. Зрозуміло, що ці явища відіграють важливу роль у повсякденному житті і суттєві при вирішенні багатьох технічних задач.

Захист твердих тіл (космічних апаратів) від згоряння і сильного оплавлення при вході з великими швидкостями в густі шари атмосфери.

Теорія турбулентних рухів рідин і газів, які є в дійсності дуже складними, нерегулярними випадкового характеру рухами. Дослідження з турбулентності до теперішнього часу не можна вважати достатніми для розуміння багатьох особливостей і закономірностей у природі таких складних рухів. Зокрема, наука про прогноз погоди – метеорологія у значній мірі являє собою вивчення турбулентних рухів повітряних мас в атмосфері Землі і є важливим розділом механіки суцільного середовища, тісно пов’язаним з багатьма іншими розділами фізики.

Значна частина курсу механіки суцільного середовища присвячена вивченню рухів і рівноваги твердих деформівних тіл. Теорія пружності є теоретичною основною для побудови різного роду споруд і всеможливих машин. Її основна задача про міцність і руйнування конструкцій із різних матеріалів на сьогодні ще не має повного розв’язку.

Згадаємо ще про механічні проблеми, які пов’язані з рухами різного роду сумішей, рухом пісків, снігів, ґрунтів, сплавів, рідких розчинів, суспензій і емульсій. Всі ці задачі актуальні як в теоретичному, так і в прикладному аспекті і потребують повного розв’язання.

Методи механіки суцільного середовища. Пропонований курс є теоретичним курсом механіки суцільного середовища. У ньому будуть розглянуті математичні методи вивчення руху рідин і деформівних твердих тіл.

Вводиться ряд понять, які характеризують і однозначно визначають рух суцільного середовища. Ці поняття повинні визначатися за допомогою чисел або інших математичних понять (поля швидкостей, тисків, температур і т.п.)

У механіці суцільного середовища розробляються методи зведення механічних задач до математичних, тобто до задач відшукання деяких чисел або числових функцій за допомогою різних математичних операцій.

Крім того, важливою метою механіки суцільного середовища є встановлення загальних властивостей і законів руху деформівних тіл.

Відзначимо, що саме розв’язування конкретних задач механіки суцільного середовища шляхом математичних операцій, як правило, відноситься до механіки суцільних середовищ. Це пояснюється тим, що навіть у найпростіших випадках математично сформульовані задачі механіки суцільного середовища виявляються дуже складними і нерозв’язними ефективно сучасними засобами математики. Тому, доводиться видозмінювати постановки задач і визначати наближені їх розв’язки на підставі різних гіпотез механіки і спрощень. Однією із основних гіпотез механіки суцільного середовища є гіпотеза суцільності.

Під суцільним середовищем будемо розуміти деяку частину тривимірного простору, яка заповнена матеріальною речовиною. Будемо також вважати, що матеріальна речовина повністю заповнює всі точки об’єму, який вона займає. Щодо природи цієї речовини, то вона може бути різною, наприклад, тверде деформівне тіло, рідина, газоподібна речовина. До суцільних середовищ можна віднести і фізичні поля (гравітаційне, магнітне, радіаційне). Суцільне середовище може і не бути матеріальним, наприклад, таким середовищем можна вважати ціни на ринку і розглядати рух такого середовища як зміну цін з часом.

В залежності від матеріального змісту речовини, рух якої вивчається в механіці суцільного середовища, виділяють такі основні розділи:

1. гідродинаміка – вивчає рухи рідин;

2. аеромеханіка або газова динаміка – вивчає рухи газів;

3. теорія пружності – вивчає рухи і рівновагу пружних деформівних твердих тіл.

В залежності від моделі суцільного середовища названі вище три розділи можуть бути поділені на декілька підрозділів, наприклад, теорія пружності поділяється на лінійну теорію пружності, теорію пластичності, теорію в’язкопружності, теорію магнітопружності та інші. Гідродинаміка поділяється на гідродинаміку ідеальної рідини і гідродинаміку реальної рідини. Аеромеханіка поділяється на аеромеханіку дозвукових швидкостей, надзвукових швидкостей і гіперзвукових швидкостей.

Рух будь-якого об’єкта завжди визначається по відношенню до деякої системи відліку – системи координат. З її допомогою встановлюється відповідність між числами і точками простору. В тривимірному просторі точкам ставляться у відповідність впорядковані трійки чисел , які називаються їх координатами відносно вибраної системи координат.

Якщо координатні лінії , , прямі, то система координат називається прямолінійною (декартовою), в інших випадках – криволінійною (рис. 1.1).

Домовимося через позначати координати точки відносно довільної, в тому числі і декартової, системи координат, а через – координати точки відносно ортогональної декартової системи координат, через – час. Рухома матеріальна точка в різні моменти часу ототожнюються з різними точками простору і її положення в просторі характеризується координатами відповідної геометричної точки, які змінюються з часом.

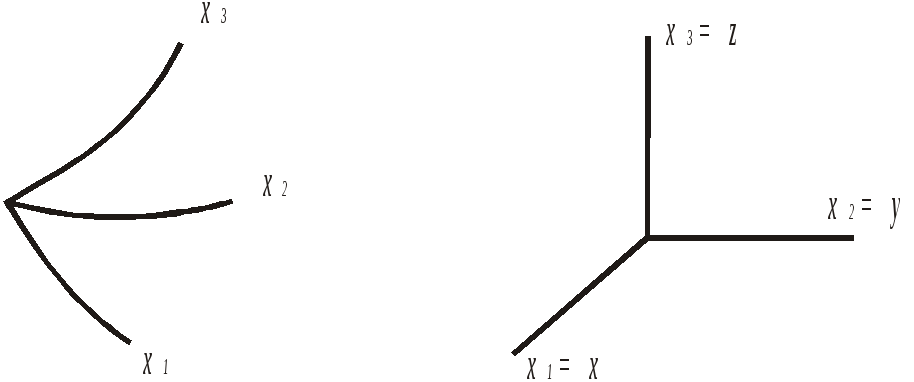
Рис. 1.1. Криволінійна і декартова системи координат