4.2. Тензор напружень

Розглянемо деяку точку деформівного тіла і довільну площадку, яка проходить через цю точку. Положення площадки визначається вектором зовнішньої нормалі .

Початок координатних осей сумістимо з точкою , в околі якої виділимо елементарний тетраедр (рис. 4.2), три грані якого проходять через точку і паралельні координатним площинам. Четверта грань перпендикулярна до вектора . Площі координатних площадок визначаються формулами

, (4.5)

де – компоненти одиничного вектора ; – площа грані, яка перпендикулярна до .

К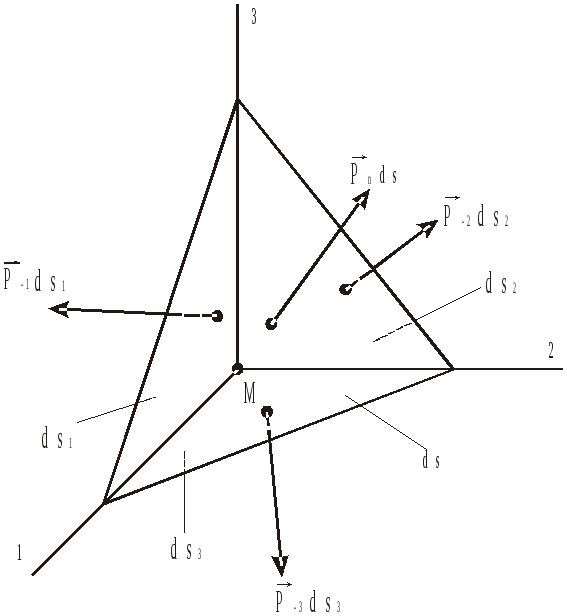рім поверхневих сил , , , , що діють на грані елемента, на нього діє об’ємна сила . Оскільки елемент, на який діють ці сили, перебуває у рівновазі, то їх головний вектор дорівнює нулю

, (4.6)

д

Рис.4.2.

е , – відстань від точки до площадки з нормаллю .

З урахуванням (4.4) і (4.5) умову (4.6) запишемо у вигляді

. (4.7)

Якщо тетраедр стягується в точку без зміни напрямку , то величина і в співвідношенні (4.7) можна відкинути доданок , тобто

. (4.8)

Таким чином, вектор напруження на довільній площадці з нормаллю , яка проходить через точку тіла, повністю визначається трьома векторами напруження на координатних площадках, що також проходять через точку .

Вектори і розкладемо за базисними векторами ():

;

;

; (4.9)

,

де – компоненти вектора напруження на довільній площадці з нормаллю ; – компоненти векторів напруження на координатних площадках.

Підставляючи (4.9) в (4.8) і порівнюючи коефіцієнти при однакових базисних векторах, знаходимо

;

; (4.10)

.

Таким чином напружений стан в заданій точці повністю задається величинами , які визначаються в точці .

На підставі оберненої тензорної ознаки дев’ять компонентів трьох векторів є компонентами тензора другого рангу, який називається тензором напружень. Його матриця має вигляд

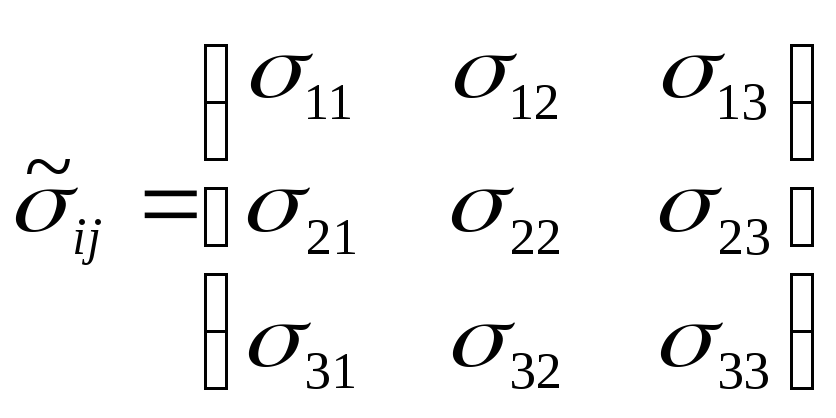, (4.11)

де діагональні елементи , , – нормальні напруження на координатних площадках, які називаються нормальними компонентами тензора , а інші елементи матриці – дотичні напруження на координатних площадках або дотичні компоненти тензора напружень.

П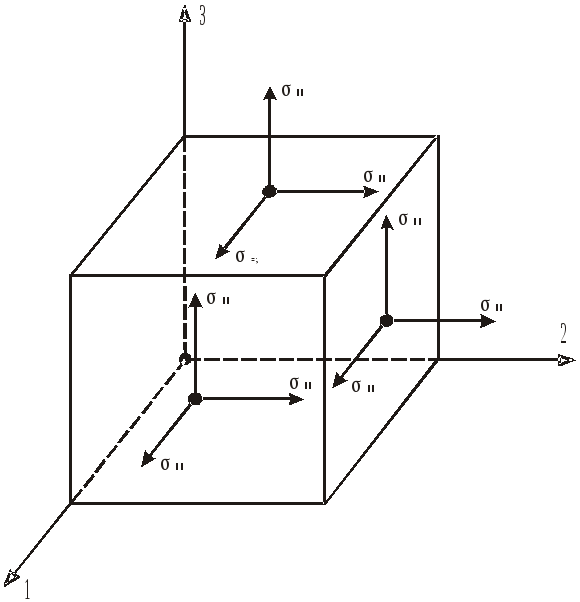ерший індекс у компонент тензора напружень відповідає індексу осі , яка перпендикулярна до координатної площадки з вектором напруження , другий індекс вказує напрямок компоненти вздовж координатної осі (рис. 4.3).

З

Рис. 4.3

ауважимо, що компоненти тензора напружень не залежать від вибору площадки, а залежать тільки від вибору точки .

4.3. Диференціальні рівняння рівноваги пружного тіла. Симетричність тензора напружень

Нехай на деформівне тіло об’ємом , який обмежений поверхнею , діють об’ємні і поверхневі сили, що викликають малі зміщення його точок, а отже, і малі деформації.

Деформівне тіло, як єдине ціле, буде перебувати у рівновазі, якщо головний вектор і головний момент об’ємних і поверхневих сил будуть дорівнювати нулю. При рівновазі тіла будь-яка, умовно виділена його частина, також повинна перебувати у рівновазі під дією сил, які до неї прикладені.

Виділимо умовно в об’ємі деякий інший об’єм , обмежений поверхнею , такий, щоб поверхні і не перетиналися (рис. 4.4).

Р

Рис. 4.4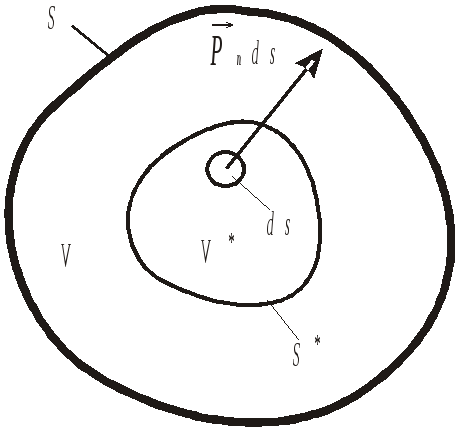

озглянемо на поверхні елемент з нормаллю , на який діє напруження . Для об’єму це напруження внутрішнє, а для – зовнішнє. Під дією поверхневих сил , а також об’ємних сил виділена частина об’ємом перебуває в рівновазі, тому на підставі (4.1), (4.2) умови рівноваги запишуться у вигляді

; (4.12)

або

; . (4.13)

Застосувавши до поверхневих інтегралів (4.13) формулу Гаусса-Остроградського

; ,

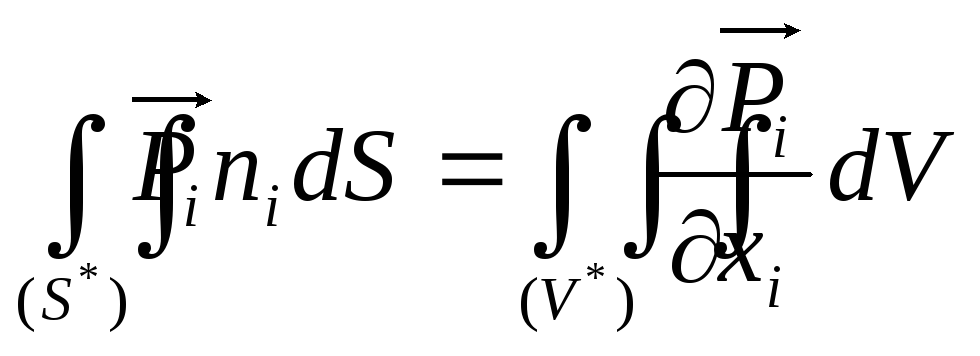одержимо

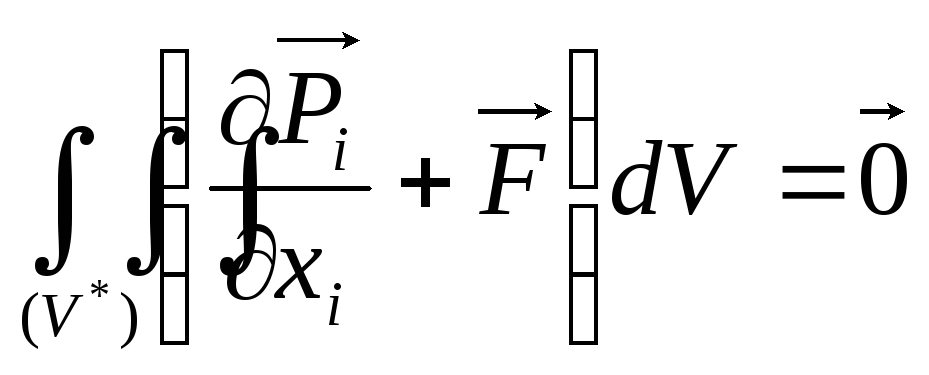; (4.14)

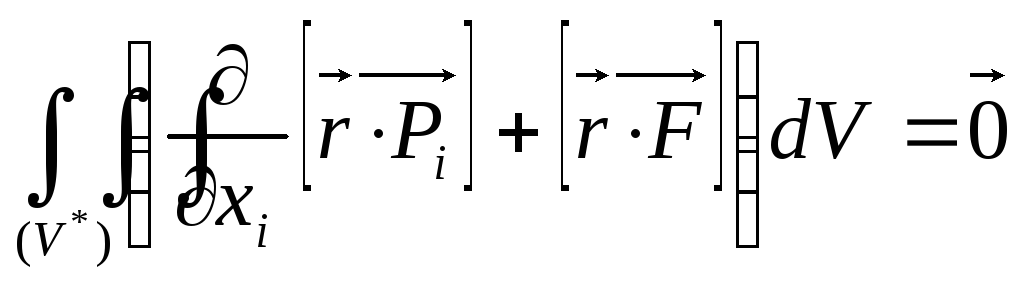. (4.15)

Умови (4.14), (4.15) повинні виконуватися для довільних об’ємів , а це можливо лише тоді, коли підінтегральні функції дорівнюють нулю

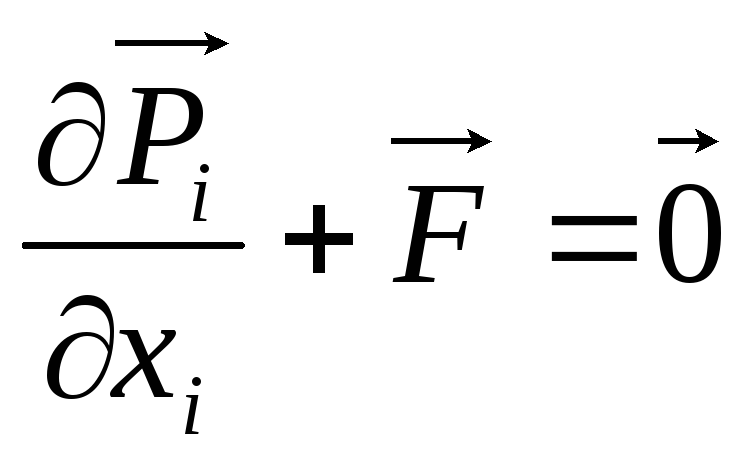; . (4.16)

Перша умова рівноваги (4.16) з врахуванням (4.9) визначає систему трьох диференціальних рівнянь рівноваги тіла

, (4.17)

або в розгорнутому вигляді

;

;

, (4.18)

де .

У тензорному вигляді диференціальні рівняння рівноваги (4.18) записуються так

. (4.19)

Другу умову рівноваги (4.16) перетворимо до вигляду

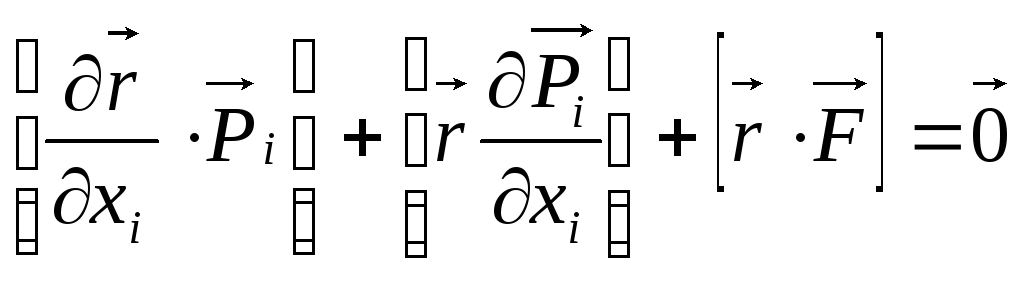
або

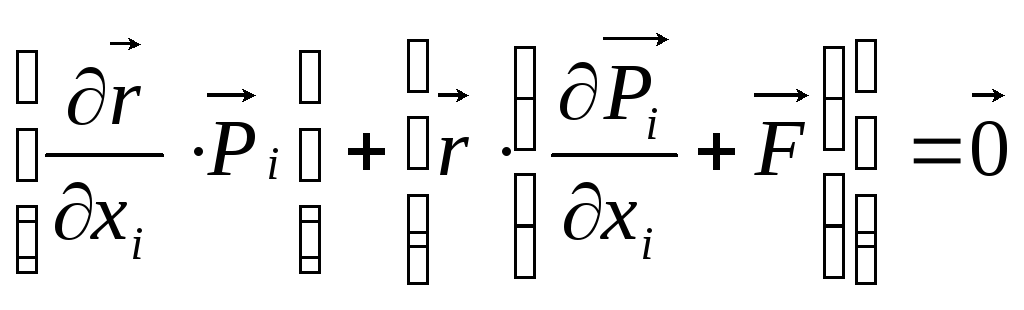. (4.20)

Другий доданок в (4.20) на підставі (4.16) дорівнює нулю, тому

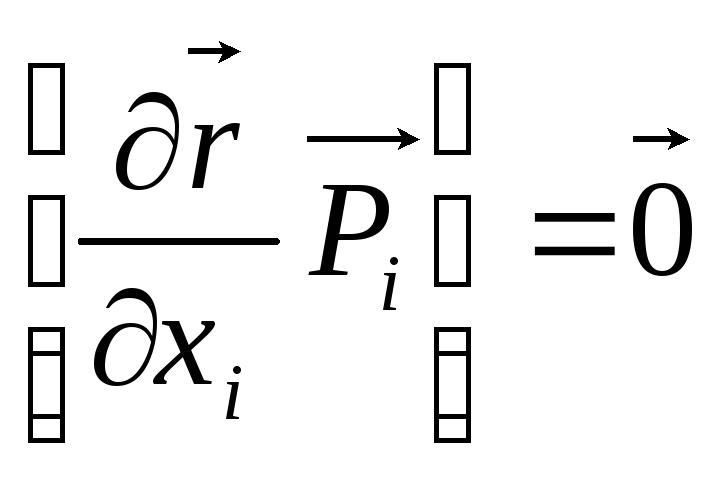. (4.21)

Враховуючи, що 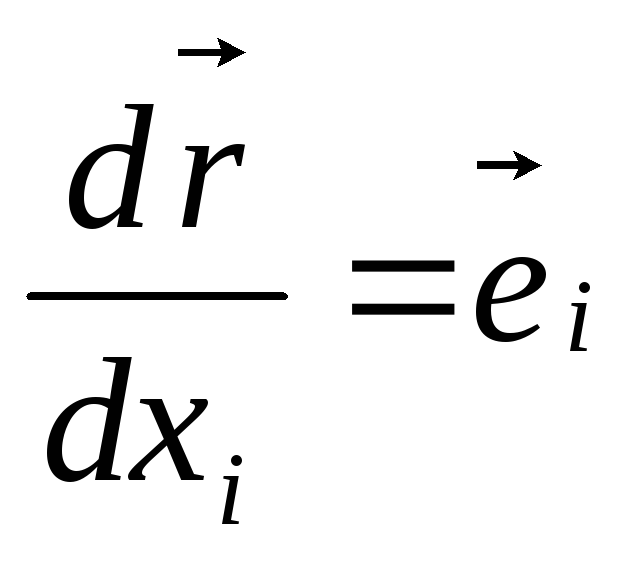, , із (4.21) одержимо

або

. (4.22)

Оскільки базисні вектори лінійно незалежні, то вирази в дужках повинні одночасно дорівнювати нулю, тобто

. (4.23)

Останні співвідношення забезпечують симетричність тензора напружень і виражають закон парності дотичних напружень, згідно з яким тензор напружень має шість незалежних компонент . Величини вважаються неперервними функціями координат довільної точки тіла, включаючи і точки його поверхні. Це означає, що функції , які задовольняють рівнянням рівноваги (4.18), повинні задовольняти рівнянням рівноваги елемента, виділеного в околі довільної точки на поверхні.

Розглянемо тетраедр, умовно виділений в околі деякої точки на поверхні тіла так, що три його грані паралельні координатним площинам, а четверта грань співпадала з поверхнею в заданій її точці. Тоді вектор буде співпадати з вектором заданих поверхневих сил .

З умов рівноваги тетраедра (4.10) одержимо

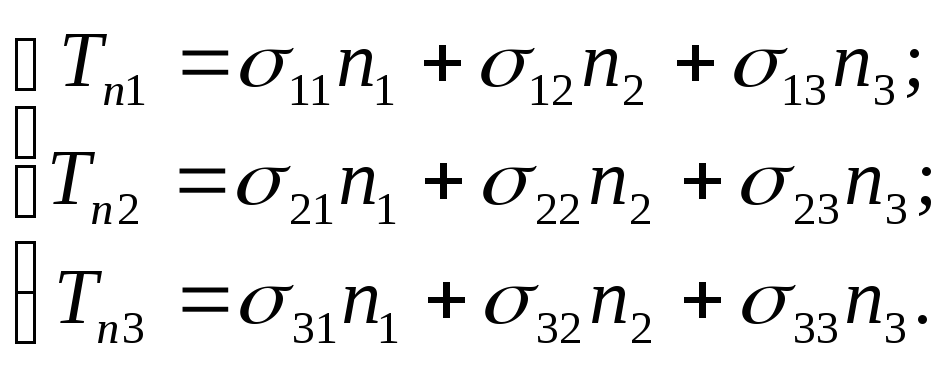(4.24)

Співвідношення (4.24), які зв’язують компоненти тензора напружень на поверхні тіла із компонентами зовнішнього поверхневого навантаження, називаються граничними умовами. У деяких випадках граничні умови визначаються заданими зміщеннями точок поверхні тіла.

При рівновазі деформованого тіла в кожній його точці шість незалежних компонент симетричного тензора напружень повинні задовольняти трьом диференціальним рівнянням рівноваги (4.18), а на поверхні тіла – граничним умовам (4.24).

Очевидно, що система трьох рівнянь (4.24), яка містить шість невідомих, має неоднозначний розв’язок, тобто задача визначення дійсного напруженого стану, викликаного заданими зовнішніми силами, статично невизначена.