
- •Задание № 1-1.
- •7. Вычислить выражения:
- •Вычислить:
- •Задание № 4-5.
- •Задание 5-4.
- •3. Вычислить определители:
- •Задание 6-2.
- •Задание № 74.
- •Задание № 8-5.
- •Задание 9-1.
- •2.Вычислить выражения:
- •4.Решить уравнение:
- •Ответы.
- •Задание 102.
- •Ответы.
- •Задание № 13 2.
- •Ответы.
- •Задание № 145.
- •Ответы.
- •Задание № 15 4.
- •Ответы .
- •Задание № 16-5.
- •Ответы.
Задание № 1-1.
1. Вычислить выражения:

2. Вычислить i38.
3. Решить систему: (1 + i)z1 + (1 i)z2 = 1+i,
(1 i)z1 + (1 + i)z2 = 1+3i .
4. Доказать, что комплексное число z является вещественным тогда
и
только тогда, когда
![]()
5. Найти комплексные числа, сопряженные своему квадрату.
6. Найти тригонометрическую форму чисел:
![]()
7. Вычислить выражения:
8. Вычислить

Ответы
1а.
15+15i;
5. 1) 0, 2) 1, 3)
 7. a) (-2)30,
b) 64.
7. a) (-2)30,
b) 64.
1б.
1; 6.
 8.
a2
ab + b2.
8.
a2
ab + b2.
Задание № 2-2.
-
Вычислить:
2. Составить таблицу умножения для группы корней 6-ой степени из 1.
3. Выписать все корни из 1 и указать первообразные для степеней 3 и 12.
4.
Решить уравнение:
![]()
Ответы.
1а.
![]() 3. № 1, 2, №1, 5, 7, 11.
3. № 1, 2, №1, 5, 7, 11.
1б.

1в.
 .
4.
.
4.
![]()
1г.
![]()
Задание № 3-2 .
-
Решить системы уравнений методом Гаусса:
а)
 б)
б)

в)
 г)
г)

д)
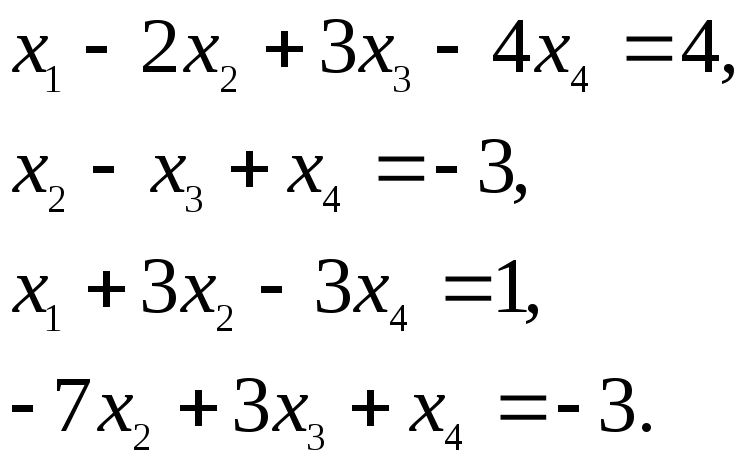 е)
е)

-
Исследовать системы и найти общее решение в зависимости от параметров:
а)
 б)
б)

в)
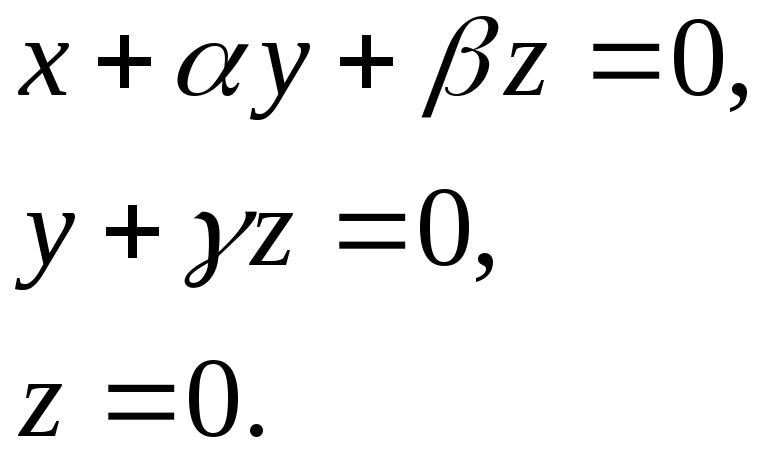 г)
г)

Ответы.
1а. x1 = 2, x2 = 1, x3 = 3, x4 = 1. 1г. Решений нет.
1б. Решений нет. 1д. х1 = 8, x2 = 3 + x4, x3 = 6 + 2x4.
1в. x1 = x2, x3 = x4 = 0. 1e. x1 = 2, x2 = x3 = x4 = 1.
2a. 0: система несовместна.
=
0:
![]()
2б. = 0, = 3: система несовместна,
0,
3:
 4
4
2в. При любых значениях параметров только нулевое решение.
2г.
При a
b
c:

Если есть пара равных: a=b, но a c, d = a или d = с (или другие сочетания), то решение зависит от одного параметра.
При a = b = c = d решение зависит от двух параметров. В других случаях решений нет.
Задание № 4-5.
1. Вычислить определители:

![]()
 .
.
2. Пользуясь
теоремой Крамера, решить системы:![]()

3. Перемножить перестановки в указанном и обратном порядке.

4. Найти перестановку x из равенства Ах = В, где
 .
.
5. Определить число инверсий в последовательностях:
а) 2, 3, 5, 4, 1; б) 6, 3, 1, 2, 5, 4; в) k, k+1, . . . , n, k-1, k-2, . . . , 2, 1.
6. Определить четность перестановок:

7. С каким знаком в определитель 6-го порядка входят произведения:
![]()
8. Какие
значения должны принимать i
и
k,
чтобы произведение
![]()
входило в определитель 9-го порядка со знаком “+“ ?, со знаком “-“ ?
9. Пользуясь определением, вычислить определитель:
 .
.
Ответы
1а. 0. 1б. 0. 1в. 2. 1г. 40. 1д. a3 + b3 + c3 3abc. 1е. 0.
2а. x = cos cos, y = cos sin. 2б. x = 1, y = 2, z = 1. 2в. x1 = 3, x2 = 4, x3 = 5.
3a.
![]() 3б.
3б.
![]() 3в.
3в.
![]() 4.
4.
![]() 5a. 5. 5б.
8. 5в.
(k
1)(n
k) + 1/2(k
1)(k
2).
5a. 5. 5б.
8. 5в.
(k
1)(n
k) + 1/2(k
1)(k
2).
6а. +(четн). 6б. +(четн). 6в. 1/2(n + 1). 7a. +. 7б. +.
8. i = 5, k = 8 , i = 8, k = 5 +. 9. abcd.
