II Which paragraph states the following?

1. A metacentric height only works for small disturbances.

2. If the upsetting moment becomes zero, the ship regains its upright position.

3. It is important to distribute the weight items of the ship with precision to avoid inclinations.

4. A submerged object rises if its weight is less than that of the displaced liquid.

5. Displacement is the weight that must be equaled by the weight of displaced water if the ship is to float.

6. The buoyant force is equivalent in magnitude to the weight of the floating object and is opposite in direction.

7. The buoyant force is closely connected with gravity.

III Answer the questions:

• What does the law of buoyancy consist in?

• What does the buoyant force depend on?

• What is the buoyant force caused by?

• Which categories of weight should be taken into account in the construction of a ship?

• What else should be considered while making a ship's draft? What problems can be caused by trim and heel inclinations? What should be done to avoid them?

• In what conditions is the ship supposed to be in static equilibrium?

• What does the resultant curve of statical stability show?

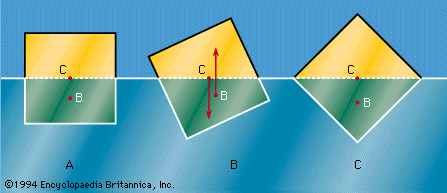
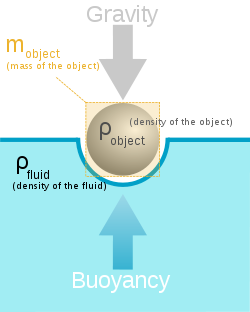
IV Using the picture (Figure I) say what forces are at work in buoyancy.

• Write down a formula showing an object flowing in equilibrium (the sum of forces on the object is zero).

• What does Figure 2 show?

Figure 2

Figure I

1. Speaking. What are the legends connected with the discovery of the Archimedes' Principle? How did he come to his discovery? What else is he famous for? Use your background knowledge or any information source you need.

2. Summarize the article in 5 – 7 sentences.

3. You are giving a lecture on the Archimedes' principle. Tell the students about the discovery and the forces that act on the submerged object.

4. You are giving a small lecture on naval construction to the students in engineering. What factors should be taken into account while making a ship draft?

Text VI Transformation of Energy: An Ideal System

A simple example of a system in which energy is being converted from one form to another is provided in the tossing of a ball with mass m into the air. When the ball is thrown vertically from the ground, it’s 1... and thus its 2... energy decreases steadily until it comes to rest momentarily at its highest point. It then reverses itself, and its speed and kinetic energy increase steadily as it returns to the ground. The kinetic energy E_k of the ball at the instant it left the ground (point 1) was half the product of the mass and the square of the 3..., or ¹/₂mv₁², and decreased steadily to zero at the highest point (point 2). As the ball rose in the air, it gained gravitational 4... energy E_p. Potential in this sense does not mean that the energy is not real but rather that it is stored in some latent form and can be drawn upon to do work. Gravitational potential energy is energy that is stored in a body by virtue of its position in the gravitational field. Gravitational potential energy of a mass m is observed to be given by the product of the mass, the height h attained relative to some reference height, and the acceleration g of a body resulting from the Earth's gravity pulling on it, or mgh. At the instant the ball left the ground at height h₁ its potential energy E_p1 is mgh₁. At its highest point, its potential energy E_p2 is mgh₂. Applying the law of 5 ... of energy and assuming no friction in the air, these add up to form the following equations:

E_k1 + E_p1 = E_k2 + E_p2, or

1/2mv₁² + mgh₁ = 0 + mgh₂

In this idealized example the kinetic energy of the ball at ground level is converted into work in raising the ball to h₂ where its gravitational potential energy has been increased by mg (h₂ - h₁). As the ball falls back to the ground level h₁, this gravitational potential energy is converted back into kinetic energy and its total energy at h₁ again is ¹/₂mv₁² + mgh₁. In this chain of events the kinetic energy of the ball is unchanged at h₁; thus the work done on the ball by the force of gravity acting on it in this cycle of events is zero. This system is said to be a conservative one.