Уравнения прямой на плоскости. Взаимное расположение двух прямых на плоскости. Условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.

Пусть на плоскости задана прямоугольная декартова система координат. Выберем произвольно точку и зададим ненулевой вектор . Найдем уравнение прямой, проходящей через точку и перпендикулярной вектору . Возьмем на искомой прямой произвольно точку отличную от точки и рассмотрим вектор . Так как вектор лежит на искомой прямой, которая должна быть перпендикулярна вектору , то утверждаем, что векторы и взаимно перпендикулярны. Значит по теореме 2 имеем . Вычислив скалярное произведение по теореме 3, получаем , или . Поскольку числа нам известны, то, обозначив число через , получим уравнение

, (1)

Так как точка выбиралась на искомой прямой, а условие является необходимым и достаточным для перпендикулярности векторов и , то утверждаем, что полученное уравнение (1) и является уравнением искомой прямой. Его называют общим уравнением прямой, а вектор называют нормальным вектором для этой прямой. Учитывая, что этот вектор ненулевой, в уравнении (1) числа и не могут одновременно равняться нулю.

Рассмотрим теперь другие уравнения прямой на плоскости.

Возьмем уравнение (1) и для определенности положим, что . Тогда поделив обе части уравнения (1) на , получим , или .

Обозначим и . Тогда уравнение (1) запишется в виде

. (2)

Число (равное тангенсу угла наклона прямой к положительному направлению оси ) называют угловым коэффициентом прямой, а уравнение (2) – уравнением с угловым коэффициентом.

Пусть теперь требуется найти уравнение прямой, если известен ее угловой коэффициент и одна точка . Для решения такой задачи воспользуемся уравнением (2), в котором неизвестен параметр . Так как точка лежит на прямой, то ее координаты должны удовлетворять уравнению (2), т.е имеет место равенство . Вычитая это уравнение из (2), получаем

. (3)

Уравнение (3) называют уравнением прямой с угловым коэффициентом и известной точкой.

Далее найдем уравнение прямой, проходящей через данную точку параллельно заданному ненулевому вектору . Для этого возьмем на искомой прямой произвольно точку отличную от точки и рассмотрим вектор . Так как вектор лежит на искомой прямой, которая должна быть параллельна вектору , то утверждаем, что векторы и коллинеарны. Следовательно по теореме 1 найдется число такое, что . Из равенства этих векторов следует равенство их одноименных координат: . Отсюда и получаем искомые уравнения прямой в виде

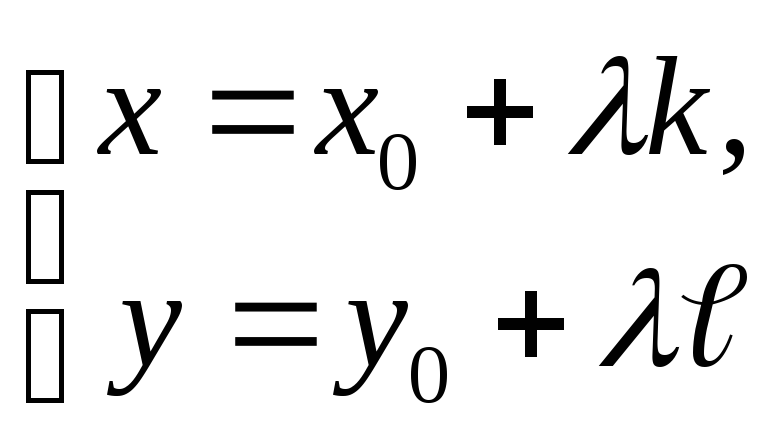(4)

В уравнениях (4) число называют параметром, а сами уравнения – параметрическими.

Если выразить параметр в каждом из уравнений (4) и приравнять, то получим уравнение прямой в виде

. (5)

Уравнение (5) называют каноническим уравнением прямой.

Если некоторый вектор параллелен прямой, то его называют направляющим вектором этой прямой. Таким образом, в каноническом уравнении (5) в знаменателях дробей левой и правой частей стоят координаты направляющего вектора .

Если в общем уравнении прямой (1) выполняются условия , то его называют полным. В противном случае уравнение (1) называют неполным. Допустим, что мы имеем полное уравнение (1). Перенесем число в правую часть и поделим обе части уравнения на . Получим , или . Обозначив , приходим к уравнению

, (6)

которое называют уравнением прямой в отрезках. Если в уравнении (6) положить , то получим . Значит, точка лежит на прямой и оси , отсекая, тем самым на этой оси отрезок длины . Аналогично точка отсекает отрезок длины на оси . Отсюда и название уравнения. Следует только иметь в виду, что если число (или ) будет отрицательным, то отрезок длины (или ) будет отсекаться на отрицательной полуоси.

И, наконец, найдем уравнение прямой, проходящей через две заданные точки и . Рассмотрим вектор . Он является направляющим вектором искомой прямой. Поэтому для решения задачи воспользуемся каноническим уравнением (5), взяв в качестве известной точки, например, точку . Получим

. (7)

Заметим, что если бы мы в качестве известной точки взяли бы точку , то получили бы уравнение в виде , которое легко приводится к уравнению (7), если к обеим частям прибавить число 1 и упростить.

Пусть на плоскости имеем прямоугольную декартову систему координат, в которой заданы прямая общим уравнением и точка , не лежащая на . Опустим из точки перпендикуляр на и обозначим основание этого перпендикуляра через .

Из того, что точка лежит на , имеем равенство . Расстоянием от точки до прямой назовем длину перпендикуляра . Поставим задачу – найти расстояние от до . Для этого рассмотрим два вектора: нормальный вектор для прямой и . Очевидно, что эти векторы коллинеарны. Следовательно, угол между ними равен либо , либо . Вычислим модуль скалярного произведения векторов и . С одной стороны, , а, с другой стороны, . Значит .

Заметив, что ,

, , получаем равенство . Отсюда расстояние от до будет равно .

Легко видеть, что если точка лежит на прямой , то расстояние от до будет равно нулю, так как .

Рассмотрим теперь вопрос о взаимном расположении двух прямых и на плоскости. Если эти прямые пересекаются, то между ними образуется четыре угла с общей вершиной в точке пересечения. При этом различных углов будет только два. Очевидно, что если один из двух различных углов равен , то другой будет равен . Углом между прямыми и будем называть любой из углов или .

Допустим, что прямые и заданы общими уравнениями и соответственно. Рассмотрим нормальные векторы и этих прямых. Легко заметить, что угол между и будет углом между прямыми и и находится из формулы .

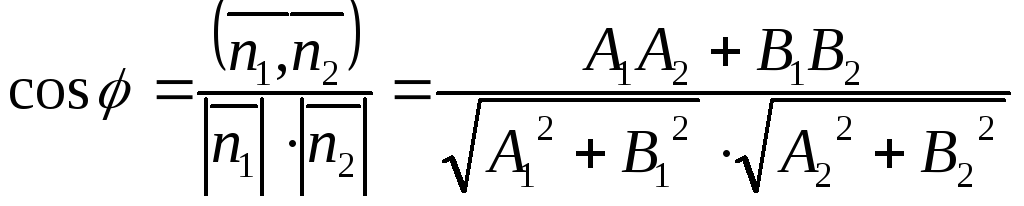На основании теоремы 2 с учетом теоремы 3 для плоскости утверждаем, что необходимым и достаточным условием перпендикулярности двух прямых и является условие .

Если прямые и параллельны, то их нормальные векторы и будут коллинеарны. По теореме 1 найдется число такое, что . Далее имеем 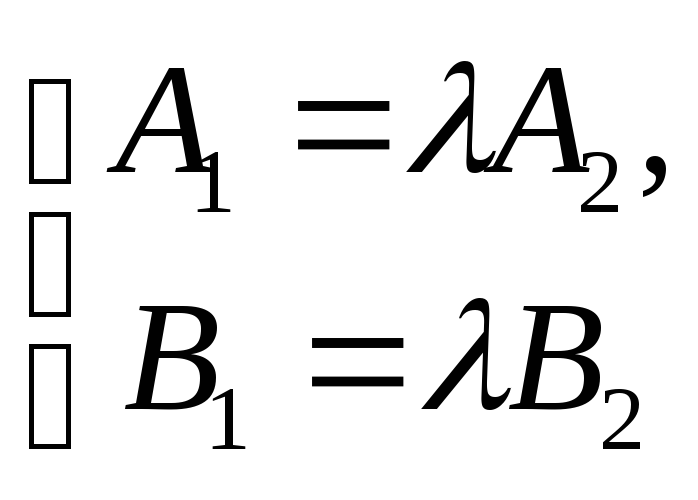. Отсюда . Итак, необходимым и достаточным условием параллельности двух прямых и является пропорциональность координат нормальных векторов: .

Рассмотрим теперь вопрос о взаимном расположении двух прямых на плоскости, если прямые и заданы уравнениями и . Обозначим через и углы между положительным направлением оси ОХ и прямыми и соответственно. Тогда и .

Угол между прямыми и может быть найден как . Тогда .

Поскольку и нам известны, то находим тангенс искомого угла и сам угол. Из полученной формулы определим условия перпендикулярности и параллельности прямых и .

Параллельность прямых и означает, что . Следовательно , или , или . Итак, для параллельности прямых и необходимо и достаточно равенство угловых коэффициентов этих прямых.

Перпендикулярность прямых и означает, что . Тогда не существует, что равносильно равенству нулю знаменателя дроби, т.е . Таким образом для перпендикулярности прямых и необходимо и достаточно, чтобы угловые коэффициенты этих прямых удовлетворяли равенству , или .