Питання для самоконтролю

1. Які дві класифікації сил застосовують у динаміці? У чому їх умовність?

2. В якій механічній системі внутрішні сили знаходяться у рівновазі?

3. Декілька автомобілів рухаються по дорозі. Чи утворюють вони механічну систему?

4. Вагон, що рухається, ударяється об нерухомий вагон. На який з них буде діяти більша сила?

5. Якими величинами характеризується розподіл мас в механічній системі?

6. Як визначається центр мас механічної системи?

7. Як визначаються і як класифікуються моменти інерції механічної системи?

8. Які осі називають головними центральними осями? Які властивості вони мають?

9. Як формулюється теорема Гюйгенса?

10. Для деякого тіла радіус інерції відносно осі , що проходить через центр мас, дорівнює . Чи є осі, які паралельні осі , відносно яких величина радіуса інерції цього тіла буде: більше ? менше ?

3.4. Загальні теореми динаміки

3.4.1. Кількість руху і теореми про зміну кількості руху матеріальної точки і системи

Однією з мір механічного руху матеріальних об’єктів є кількість їх руху, або імпульс.

Кількістю руху (імпульсом) матеріальної точки називається векторна величина, яка дорівнює добутку маси точки на вектор її швидкості, тобто:

.

Кількістю руху (імпульсом) механічної системи називають вектор, рівний геометричній сумі векторів кількостей руху (імпульсів) всіх матеріальних точок системи:

.

(3.58)

На відміну від кількості руху точки, який є зв’язаним вектором, вектор кількості руху механічної системи є вільним вектором.

В системі СІ кількість руху має розмірність Н·с, або .

Для обчислення кількості руху механічної системи дещо перетворимо вираз (3.58):

.

В свою чергу з визначення центра мас системи виходить, що

і .

Тоді:

.

(3.59)

Таким чином, вектор кількості руху механічної системи дорівнює добутку маси системи на вектор швидкості її центра мас.

Доцільно зауважити, що вектор , подібно до головного вектора сил в статиці, є певною узагальненою характеристикою руху всієї механічної системи. В загальному випадку кількість руху можна розглядати як характеристику поступальної частини руху системи разом з її центром мас.

При практичних розрахунках доцільно користуватися алгебраїчними рівняннями, що виходять з (3.59):

, , .

(3.60)

Звідсіля величина кількості руху:

.

(3.61)

Як відомо з курсу фізики, міру дії сили на матеріальну точку за елементарний проміжок часу називають елементарним імпульсом сили , тобто:

.

(3.62)

Імпульс сили за кінцевий проміжок часу визначають за формулою:

.

(3.63)

Модуль імпульса сили підраховують за його проекціями на координатні осі:

і .

(3.63')

Основний закон динаміки можна записати у формі:

.

(3.64)

Проінтегруємо це рівняння в межах часу від до і отримаємо:

.

(3.65)

Рівняння (3.65) називають теоремою імпульсів в кінцевій формі:

зміна кількості руху точки за деякий проміжок часу дорівнює імпульсу рівнодіючої сил, прикладених до точки, за той же проміжок часу.

При розв’язанні задач користуються рівняннями цієї теореми в проекціях на координатні осі.

(3.66)

Тепер розглянемо механічну систему, що складається з n матеріальних точок. Для кожної з цих точок згідно з (3.56) можна записати:

, .

Підсумуємо такі рівняння по всіх точках системи і з урахуванням відомого положення, що сума похідних дорівнює похідній від суми, отримаємо:

Так як для внутрішніх сил , а , то маємо:

(3.67)

Останній вираз є математичним записом теореми про зміну кількості руху механічної системи в диференіальній формі: в кожний момент часу похідна за часом від вектора кількості руху системи дорівнює геометричній сумі всіх зовнішніх сил, що діють на систему.

В декартових координатах математичний вираз теореми такий:

; ; .

(3.68)

Помножимо обидві частини рівняння (3.67) на і проінтегруємо в межах часу до :

,

звідкіля:

.

(3.69)

Ми отримали математичну формулу теореми про зміну вектора кількості руху механічної системи в інтегральному (кінцевому) вигляді. Теорема стверджує, що зміна вектора кількості руху системи за будь-який проміжок часу дорівнює геометричній сумі імпульсів усіх зовнішніх сил, які діють на систему, за той же час.

В проекціях на координатні осі будемо мати:

; ; .

(3.70)

З теореми про зміну кількості руху механічної системи можна отримати важливі висновки, які називають законом збереження кількості руху системи.

1. Якщо геометрична сума всіх зовнішніх сил, що діють на систему, дорівнює нулю, то вектор кількості руху її буде сталим як за величиною, так і за напрямом.

Дійсно, при з рівняння (3.67) виходить, що:

і, відповідно .

2. У випадках, коли сума проекцій зовнішніх сил, прикладених до системи, на деяку нерухому вісь дорівнює нулю, то проекція кількості руху системи на цю вісь залишається незмінною.

Так, наприклад, при і (див. перше рівняння системи 3.68).

Доцільно зауважити, що закон збереження кількості руху зручно використовувати в тих випадках, коли по зміні швидкості однієї частини системи потрібно визначити швидкість її другої частини.

Теоремі про зміну кількості руху механічної системи можна надати ще одну форму, яка зветься теоремою про рух центра мас.

Якщо врахувати, що , то рівняння (3.67) набуває вигляду:

,

або, при сталій масі,

,

(3.71)

де - вектор прискорення центра мас системи.

Рівняння (3.71) – це математичний запис теореми про рух центра мас системи: центр мас механічної системи рухається так само, як матеріальна точка, в якій зосереджена маса всієї системи, під дією головного вектора зовнішніх сил.

В проекціях на осі декартової системи координат теорема записується системою рівнянь:

(3.72)

де - координати центра мас системи.

Внутрішні сили у відповідності з викладеним не впливають на рух центра мас. Тому, наприклад, людина не може пересуватись на абсолютно гладкій поверхні за допомогою лише зусиль своїх м’язів. Рушійна сила тепловоза або трамвая виникає тільки при наявності тертя. Сили тертя в даному випадку повинні бути віднесені до зовнішніх сил.

З теореми виходять такі висновки:

1. Якщо головний вектор зовнішніх сил, що діють на систему, дорівнює нулю, то центр мас системи перебуває в стані спокою або рухається прямолінійно і рівномірно.

Дійсно, при :

і .

2. Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку нерухому вісь дорівнює нулю, то проекція швидкості центра мас на цю вісь є сталою величиною.

Наприклад, якщо , то:

і .

3. У випадку, коли проекція головного вектора зовнішніх сил, що діють на систему, на деяку нерухому вісь дорівнює нулю, а центр мас системи був нерухомий відносно цієї осі в початковий момент часу, то положення центра мас відносно осі буде сталим в будь-який момент часу.

Тому алгебраїчна сума добутків мас окремих тіл системи на проекції абсолютних переміщень центрів мас цих тіл відносно даної осі повинна дорівнювати нулю. Так, якщо викладене стосується осі , то:

(3.73)

При обчисленні абсолютних переміщень треба завжди враховувати їх знаки в обраній системі відліку.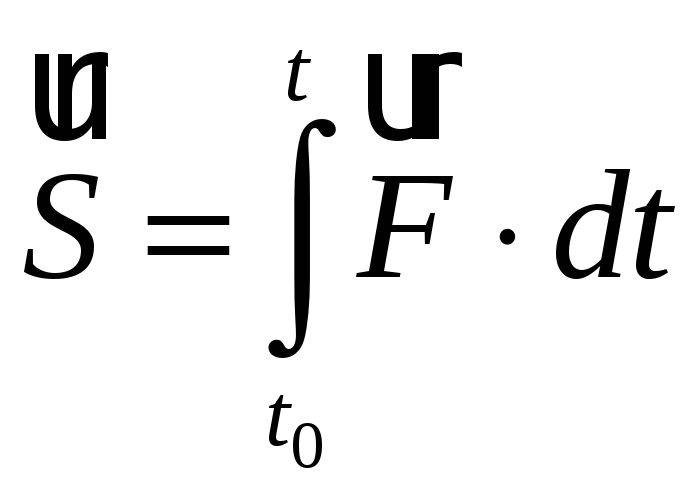