Теорема Гюйгенса

Моменти інерції даного тіла відносно різних осей будуть мати різні значення. Залежність між моментами інерції тіла відносно двох паралельних осей визначається теоремою Гюйгенса:

момент інерції механічної системи (твердого тіла) відносно будь-якої осі дорівнює сумі момента інерції відносно осі, що проходить через центр мас цієї системи (тіла) паралельно даній, і добутку маси системи на квадрат відстані між цими осями.

Припустимо, що відомий момент інерції тіла відносно осі , яка проходить через центр мас тіла. Визначимо момент інерції цього тіла відносно осі , проведеної паралельно до на відстані «d» від неї (рис.3.15). Оберемо довільну точку К тіла масою , яка відстоїть від центральної осі на відстані і на відстані - від осі .

Рис. 3.15

Утворений трикутник з кутом буде паралельним площині (а також ).

З трикутника за теоремою косинусів отримаємо:

Помножимо кожний член цього співвідношення на масу ї точки і просумуємо по всіх точках тіла:

Оскільки:

і , то:

.

Але 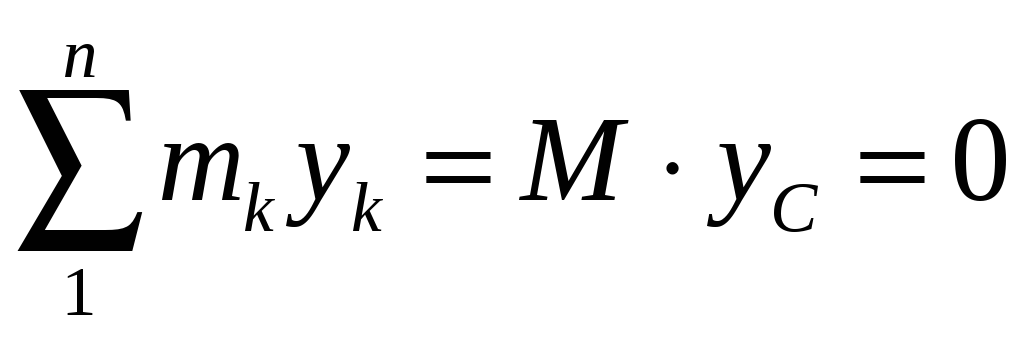, бо в нашому випадку координата центра мас тіла .

Таким чином, кінцево маємо:

,

(3.55)

що і потрібно було довести.

Обчислення осьових моментів інерції деяких однорідних тіл

1. Тонкий однорідний стержень довжиною і масою .

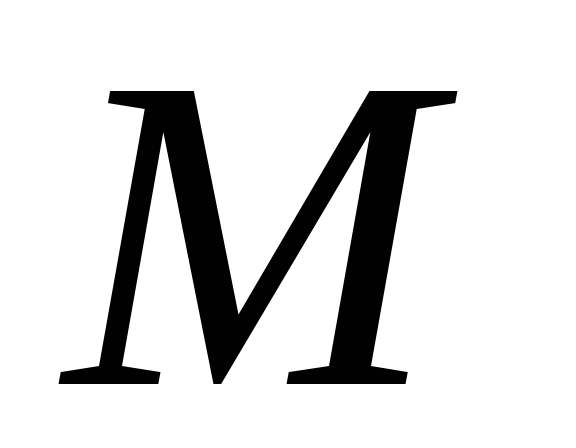Підрахуємо момент інерції стержня відносно осі , що проходить через його кінець перпендикулярно до осі стержня. Координатну вісь направляємо вздовж (рис.а).

Оскільки стержень однорідний, то маса елементарного відрізка довжиною , який знаходиться на відстані від осі , .

Тоді згідно з формулою (3.50'):

.

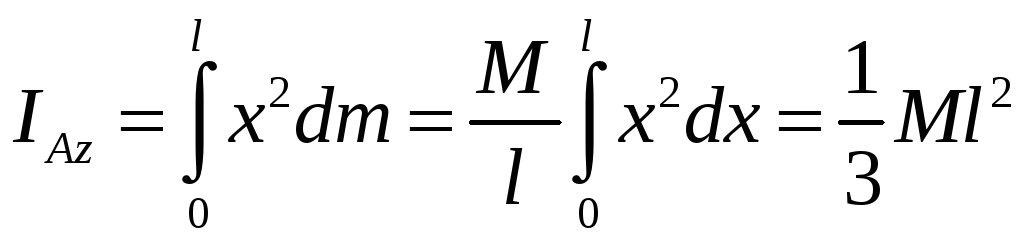
Рис. а

2. Тонке однорідне кільце маси М і радіуса R.

Визначимо момент інерції кільця відносно осі , що проходить через його центр мас С перпендикулярно до площини кільця (рис. б). Так як всі елементарні маси кільця знаходяться на однаковій відстані R від осі Сz, то:

.

Рис. б

3. Кругла однорідна пластина чи циліндр радіуса R і маси M.

Підрахуємо момент інерції круглої пластини відносно осі , перпендикулярної до пластини (рис. в). Площа елементарного кільця радіуса і шириною дорівнює . Маса одиниці площі . Тоді маса елементарного кільця , а момент інерції .

Для всієї пластини :

.

Момент інерції для однорідного круглого циліндра масою М і радіусом R відносно його поздовжньої центральної осі (рис. г) буде визначатися такою ж формулою.

Рис. в

Рис. г

0. 3.3.4. Диференціальні рівняння руху механічної системи

Розглянемо механічну систему, що складається з «n» матеріальних точок. Використаємо принцип звільнення від в’язей і замінимо в’язі їх реакціями. Всі сили, що діють на систему, поділимо на зовнішні і внутрішні. Тоді для довільної точки k системи масою на підставі основного закону динаміки отримаємо:

,

(3.56)

де - рівнодіючі зовнішніх сил, які діють на - ту точку.

Аналогічного виду рівняння отримаємо і для будь-якої точки системи. Тобто всього для заданої системи будемо мати n таких рівнянь ().

Така система рівнянь і є диференціальними рівняннями руху механічної системи у векторній формі.

Якщо спроектувати n рівнянь (3.56) на осі обраної системи координат, то отримаємо систему алгебраїчних диференціальних рівнянь руху системи в проекціях на осі.

Наприклад, при використанні декартової системи координат будемо мати 3n скалярних рівнянь виду:

(3.57)

Як можна бачити, для визначення руху механічної системи за заданими силами і початковими умовами необхідно проінтегрувати систему з 3n диференціальних рівнянь. Цю задачу не завжди можна розв’язати точно навіть для однієї точки. Вона виключно складна у випадку двох матеріальних точок, що рухаються під дією сил взаємодії за законом всесвітнього тяжіння, і зовсім не може бути розв’язана при взаємодії трьох точок.

Інколи з диференціальних рівнянь (3.57) можна отримати так звані перші інтеграли, тобто співвідношення, до яких не входять похідні другого порядку від координат за часом. До таких перших інтегралів відносяться закони збереження механічного руху і загальні теореми динаміки системи матеріальних точок.

Завдяки впровадженню спеціальних сумарних характеристик руху всієї системи в цілому, які мають наочний фізичний зміст, загальні теореми динаміки є ефективним апаратом механіки і широко використовуються в інженерних розрахунках.

При цьому необхідно пам’ятати, що у математичні вирази цих теорем, а також до формул, що є висновками з загальних теорем, входять абсолютні швидкості і абсолютні прискорення.