3.2.3.2. Згасаючі коливання матеріальної точки

Розглянута нами теорія вільних прямолінійних коливань матеріальної тачки зовсім не враховує опору, що виникає в дійсності при її русі в навколишньому середовищі.

Нехай точка М, масою m, перебуває під дією відновлюючої сили і сили опору середовища, пропорційної першому ступеню швидкості точки: . Припустимо, що коливання точки відбуваються вздовж осі (рис.3.8). Тоді і і диференціальне рівняння руху точки буде мати вигляд:

.

Рис.3.8

Поділимо це рівняння на m і застосуємо позначення:

.

(3.30)

З урахуванням уведених позначень диференційне рівняння дістає вигляду:

.

(3.31)

Цьому диференційному рівнянню відповідає характеристичне рівняння

,

яке має корені:

.

(3.32)

Кінцевий вигляд загального розв’язку рівняння (3.31) суттєво залежить від співвідношення величин n і k . Тут можливі три випадки.

1. n<k (випадок малого опору). Корені уявні:

.

Тому загальний інтеграл рівняння (3.31) буде:

,

(3.33)

або

.

(3.33')

Сталі інтегрування , , А і визначаються з початкових умов:

; ; ; .

Вираз - колова частота згасаючих коливань.

Період згасаючих коливань:

(3.34)

не залежить від початкових умов і зберігає сталу величину.

Величина називається декрементом коливань. Графічне зображення згасаючих коливань дано на рис.3.9.

Рис.3.9

2. n>k (випадок великого опору середовища).

Корені характеристичного рівняння (3.32) дійсні і різні. Загальний інтеграл рівняння (3.31) набуває вигляду:

,

(3.35)

Сталі інтегрування і визначаються з початкових умов (). Маємо:

,

де: .

Рух, що визначається рівнянням (3.35) не є коливальним, а зображує собою аперіодичний затухаючий рух (рис.3.10).

Рис.3.10

3. n=k (граничний випадок). Корені характеристичного рівняння (3.32) . Розв’язок диференціального рівняння (3.31) буде таким:

.

(3.36)

Сталі інтегрування:

.

І в цьому випадку рух не буде коливальним; це аперіодичний згасаючий рух.

3. Вимушені коливання без урахування опору середовища

Коливальний рух матеріальної точки називається вимушеним, коли на неї, крім відновлюючої сили , діє певна збурююча сила , що є функцією часу.

В техніці найчастіше доводиться зустрічатись з випадками, коли збурююча сила є періодичною виду ( Н – амплітуда збурюючої сили, р – колова частота її).

Якщо коливання відбуваються вздовж осі х (рис.3.11), то диференціальне рівняння руху точки має вигляд:

.

(3.37)

Рис. 3.11

Застосовуємо позначення:

, .

Тоді одержимо:

.

(3.38)

Загальне розв’язання лінійного неоднорідного диференційного рівняння складається з інтеграла однорідного рівняння, що відповідає (3.38), і частинного розв’язку (3.38). Тобто:

.

Загальний інтеграл однорідного диференційного рівняння:

.

Частинний розв’язок шукаємо у вигляді:

.

Для визначення коефіцієнта В підставимо вирази і в рівняння (3.38). Знаходимо:

.

Тоді:

(3.39)

і загальне розв’язання рівняння (3.31) буде таким:

.

(3.40)

Отже, при одночасній дії відновлюючої і збурюючої сил матеріальна точка здійснює рух, складений з двох гармонійних коливань: власного або вільного коливання і вимушеного коливання.

З формули (3.38) видно, що амплітуда вимушених коливань:

.

(3.41)

Легко бачити, що при амплітуда вимушених коливань зростає, а при . Це явище називають резонансом.

Якщо вимушені коливання об’єкта спричиняються відцентровою силою інерції, яка виникає внаслідок обертання незрівноваженої маси, то кутова швидкість обертання цього об’єкту є коловою частотою збурюючої сили, тобто .

Кутова швидкість , що відповідає резонансу, називається критичною. При відсутності опору . Таким чином, для визначення критичного числа обертів двигуна необхідно знайти тільки колову частоту вільних коливань пружної опори установки.
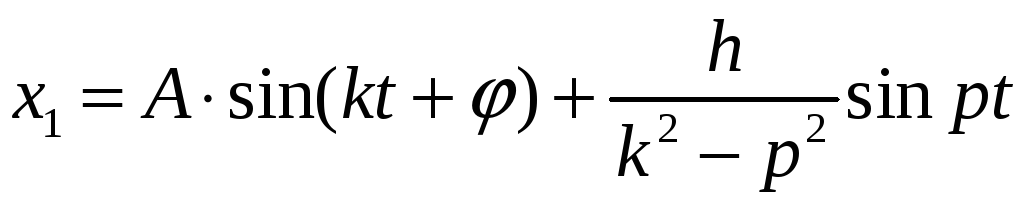