3.2.3. Прямолінійні коливання матеріальної точки

З коливальним рухом матеріальних тіл і систем доводиться дуже часто зустрічатися в техніці. Коливальний рух здійснюють окремі елементи машин, механізми і споруди. Іноді вібрації досягають значної величини і стають неприпустимими з погляду міцності та нормальної роботи машини чи споруди. Причому переважна більшість аварійних ситуацій виникає через неправильне урахування та похибки при розрахунках коливальних систем.

З другого боку, коливання з успіхом використовуються для розробки різноманітних машин і механізмів вібраційної дії (машини ущільнення бетона сортування, транспортування, тощо).

Сучасна теорія коливань – основа значної кількості задач техніки, фізики та інших наук – це велика і складна галузь механіки.

В нашому курсі ми обмежимося розглядом найпростішого коливального процесу – прямолінійних коливань матеріальної точки – як приклада застосування диференційних рівнянь (3.4) динаміки.

3.2.3.1. Вільні коливання матеріальної точки

Серед різних сил, які можуть діяти на матеріальну точку, особливе місце займають відновлюючі сили, тобто сили, які намагаються повернути точку в положення рівноваги. Такі сили залежать від відхилення точки від положення рівноваги і завжди напрямлені в бік, протилежний відхиленню.

Природа цих сил вельми різноманітна, але всі вони надають рухові матеріальної точки коливальний характер.

Найбільш прості для дослідження ті випадки, коли відновлююча сила пропорційна величині відхилення точки від положення рівноваги. Тоді (рис.3.2):

,

(3.11)

де - сталий коефіцієнт, що має розмірність Н/м; - вектор відхилення точки від положення рівноваги (центр О на рисунку).

Рис.3.2

Якщо відновлююча сила обумовлена пружними властивостями матеріального об’єкта (пружина, стержень) при його деформуванні, то коефіцієнт С називають коефіцієнтом пружності або коефіцієнтом жорсткості.

Коливальний рух матеріальної точки, який відбувається тільки під дією відновлюючої сили, пропорційної величині відхилення її від положення рівноваги, називається вільним.

Розглянемо точку М, масою m, що рухається вздовж осі x під дією відновлюючої сили (рис.3.3).

Рис. 3.3

Уданому випадку система (3.4) зводиться до одного рівняння, яке з урахуванням напряму відновлюючої сили, буде мати вигляд:

,

(3.12)

Поділимо його на m і позначимо

.

(3.13)

Тоді отримаємо рівняння:

.

(3.14)

Наведене рівняння є лінійним диференціальним рівнянням другого порядку зі сталими коефіцієнтами, характеристичне рівняння якого буде таким:

.

Оскільки корені його , уявні, то загальний інтеграл (загальний розв’язок) рівняння (3.14) відповідає рівнянню:

.

(3.15)

Сталі інтегрування і знаходимо з початкових умов руху. Хай при . З рівняння (3.1) при знаходимо: . Щоб знайти сталу , продиференціюємо за часом (3.14):

.

(3.16)

Звідкіля при визначимо: .

Таким чином, закон вільних коливань матеріальної точки при заданих початкових умовах дається співвідношенням:

.

(3.17)

Якщо замість сталих і впровадити нові сталі і , такі, що , , то закон вільного коливального руху точки можна записати у вигляді:

.

(3.18)

Стала , що дорівнює найбільшому відхиленню точки від положення рівноваги, називається амплітудою коливань.

.

(3.19)

Вираз - фаза коливань, а стала - початкова фаза.

.

(3.20)

Величину з (3.13) називають частотою вільних коливань (колова частота):

, .

(3.21)

Період вільних коливань:

,

(3.22)

Частота коливань (кількість коливань за одиницю часу):

.

(3.23)

З формул (3.21) і (3.22) видно, що колова частота і період вільних коливань не залежать від початкових умов. Характер вільних коливань точки показано на рис. 3.4.

Рис.3.4

До рівняння (3.14) приводить і випадок вертикальних коливань вантажу , що підвішений на пружині жорсткістю (рис.3.5).

- довжина недеформованої пружини; - статичне видовження пружини під дією сили ; - поточне відхилення вантажу від положення центра коливань (положення рівноваги вантажу на пружині); - повне поточне видовження пружини ; - поточна довжина деформованої пружини; - положення статичної рівноваги пружини.

На вантаж діють дві сили: сила ваги і сила пружності пружини .

Рис.3.5

Очевидно, що в положенні статичної

рівноваги відносно осі , тому:

і .

(3.24)

Диференціальне рівняння руху вантажу буде мати вигляд:

,

тобто воно співпадає з рівнянням (3.14).

Статична деформація пружини, як виходить з (3.24),

.

(3.25)

Колова частота коливань вантажу на пружині може бути визначена за формулою:

.

(3.26)

Період вільних коливань:

.

(3.27)

Ми розглянули випадок вільних коливань вантажу, що був прикріплений до однієї пружини. Розглянемо ще два випадки.

1. Вантаж, підвішений до послідовно з’єднаних пружин з різними жорсткостями (рис.3.6).

Рис. 3.6

Очевидно, що загальна деформація пружин у стані рівноваги:

.

Маючи на увазі, що , знаходимо:

.

(3.28)

2. Вантаж, підвішений до паралельно з’єднаних пружин (рис.3.7)

Загальна статична деформація пружини:

При статичній рівновазі вантажу:

Еквівалентна жорсткість двох паралельно з’єднаних пружин:

(3.29)

Рис. 3.7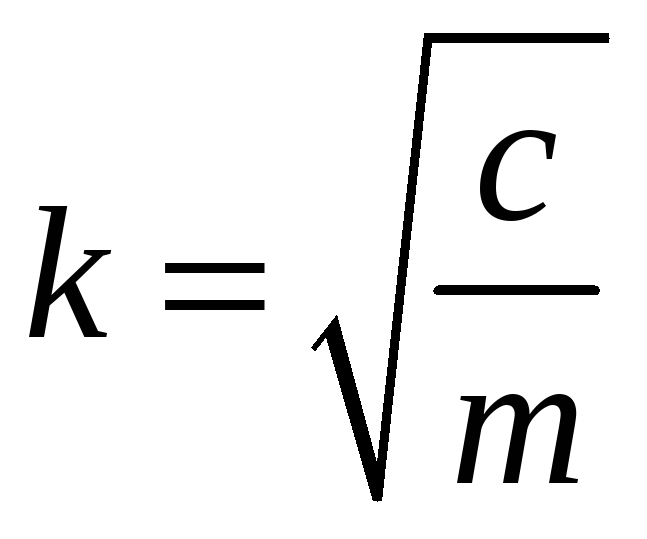
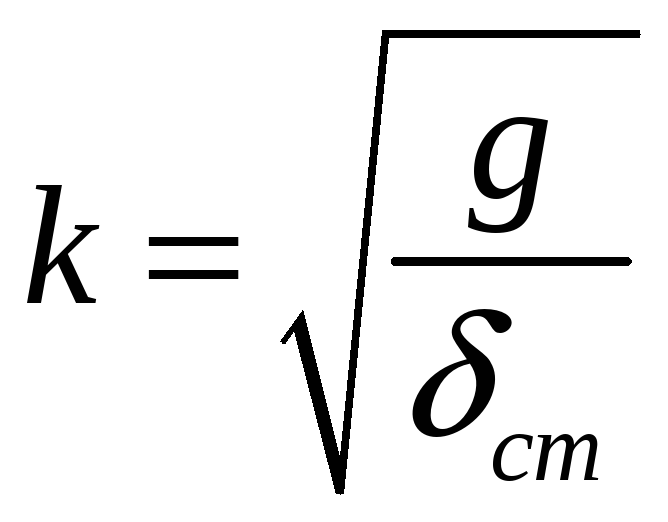