4.4.5. Диференціальні рівняння руху механічної системи в узагальнених координатах (рівняння Лагранжа другого роду)

Найбільш простим і універсальним методом дослідження руху механічної системи з одним ступенем вільності є використання теореми про зміну кінетичної енергії. Якщо ж система має декілька ступенів вільності, а в’язі є нестаціонарними, то лише однієї теореми про зміну кінетичної енергії недостатньо для повного розв’язання задачі.

Процес складання диференціальних рівнянь руху таких систем і їх розв’язок значно спрощуються при використанні диференціальних рівнянь в узагальнених координатах, які називають рівняннями Лагранжа другого роду.

Рівняння Лагранжа другого роду, які по своїй суті є рівнянням динаміки Даламбера-Лагранжа, записаним в узагальнених координатах, дають загальний метод складання диференціальних рівнянь руху механічної системи з голономними ідеальними утримуючими в’язями.

Для спрощення отримаємо ці рівняння на прикладі механічної системи з одним ступенем вільності, коли в’язі, накладені на систему, є не тільки голономні ідеальні і утримуючі але і стаціонарні.

Оскільки в’язі ідеальні, то сума елементарних робіт їх реакцій дорівнює нулю, і теорема про зміну кінетичної енергії такої системи має вигляд:

,

де - сума елементарних робіт активних сил, що діють на систему.

Припустимо, що положення системи визначається узагальненою координатою , тоді на підставі формули (4.38)

,

де - узагальнена сила, яка відповідає узагальненій координаті , теорему про зміну кінетичної енергії можна записати так:

.

(4.42)

Виразимо кінетичну енергію системи через узагальнену координату і узагальнену швидкість .

За визначенням

.

При голономних стаціонарних в’язях радіуси-вектори точок системи є функціями тільки узагальненої координати:

,

тому :

і кінетична енергія системи

.

З останнього співвідношення виходить, що кінетичну енергію системи можна розглядати як функцію двох змінних: і , тобто

,

а її диференціал

.

(4.43)

Перетворимо другу складову правої частини таким чином:

. (цей вираз виходить з того, що )

(4.44)

Визначимо добуток, що стоїть під знаком диференціала в першому доданку правої частини рівняння (4.44).

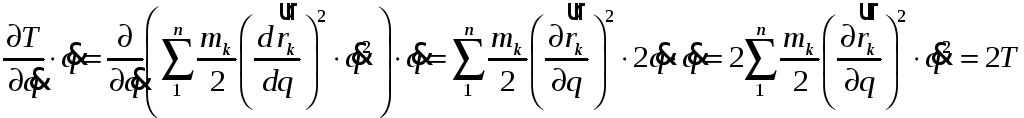
Тоді (4.44) набуває вигляду:

,

а рівняння (4.43) запишеться так:

.

Після зведення подібних отримаємо:

.

(4.45)

З урахуванням отриманого результата теорема про зміну кінетичної енергії (рівняння 4.42) набуває вигляду:

або

.

(4.46)

Оскільки диференціал узагальненої координати при русі системи не може бути тотожним нулю, то, очевидно,

,

звідкіля:

.

(4.47)

Рівняння (4.47) і є рівнянням Лагранжа другого роду для механічної системи з одним ступенем вільності, на яку накладені голономні ідеальні утримуючі і стаціонарні в’язі.

Для механічних систем з голономними утримуючими в’язями, що мають ступенів вільності, рух описується системою аналогічних рівнянь, кількість яких відповідає числу ступенів вільності. При цьому кожній узагальненій координаті відповідає своє рівняння:

, .

(4.48)

Якщо всі сили, що діють на механічну систему, потенціальні, то узагальнені сили

і рівняння Лагранжа другого роду набувають вигляду:

.

(4.49)

Оскільки потенціальна енергія не залежить від узагальнених швидкостей, то

.

Тому рівняння (4.29) можна записати так:

.

(4.50)

Впровадимо у розгляд функцію

,

(4.51)

яку називають функцією Лагранжа або кінетичним потенціалом. Тоді рівняння Лагранжа набуває вигляду:

.

(4.52)

Як найпростіший приклад, розглянемо методику складання рівнянь Лагранжа для отримання закону руху математичного маятника, що складається з вантажу масою , підвішеного на нерозтяжній нитці довжиною .

Система має один ступінь вільності. За узагальнену координату візьмемо кут відхилення нитки маятника від вертикалі. Єдина сила, що діє на систему, - сила ваги вантажу – є потенціальною. Тому для розв’язування задачі маємо одне рівняння Лагранжа у формі (4.52):

.

Виразимо кінетичну і потенціальну енергію маятника через узагальнену координату і узагальнену швидкість . Знаходимо: ,

Тому функція Лагранжа

Визначаємо:

; ; .

Підставляємо отримані результати у вихідне рівняння Лагранжа і отримуємо рівняння руху математичного маятника:

або .