4.3. Загальне рівняння динаміки

Принцип можливих переміщень дає загальний метод розв’язання задач статики. З другого боку, принцип Даламбера дозволяє використовувати методи статики для розв’язання задач динаміки матеріальних об’єктів.

Розглянемо механічну систему, яка складається з матеріальних точок і на яку накладено геометричні, стаціонарні і ідеальні в’язі. Прикладемо до всіх точок системи активні сили , реакції в’язей і сили інерції . Тоді згідно з принципом Даламбера для системи в цілому будемо мати:

.

Якщо до цього співвідношення використати принцип можливих переміщень і урахувати, що , то отримаємо:

.

(4.18)

Тобто, в кожний момент руху механічної системи з геометричними, стаціонарними і ідеальними в’язями сума можливих робіт активних сил і сил інерції на будь-якому елементарному можливому переміщенні системи повинна дорівнювати нулю.

Рівняння (4.18) називають рівнянням Лагранжа-Даламбера або загальним рівнянням динаміки. В алгебраїчній формі воно набуває вигляду:

.

(4.19)

Так як до рівняння (4.19) входить робота сил інерції, величина яких виражається через прискорення точок, то це дає змогу складати диференціальні рівняння руху механічної системи.

4.4. Рівняння Ланранжа другого роду

4.4.1. Силове поле

Силовим полем називають область (частину простору), в якій сила, що діє на матеріальну точку, однозначно визначається за величиною і напрямом в будь-який момент часу, тобто залежить лише від координат точки в обраній системі відліку і, можливо, від часу.

Силове поле, в якому сила, що діє на матеріальну точку, не залежить від часу, називається стаціонарним.

Для стаціонарних силових полів (рис.4.4), або в проекціях на осі декартової системи координат:

.

(4.20)

Поле, в якому сила не залежить від положення точки, називається однорідним.

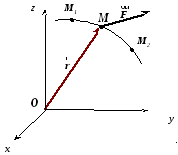
Рис. 4.4.

Стаціонарне поле називається потенціальним якщо існує деяка скалярна функція , диференціал якої дорівнює елементарній роботі сили поля , тобто:

.

(4.21)

Функцію називають потенціальною або силовою функцією чи просто потенціалом сили.

Оскільки повний диференціал функції

,

то з порівняння двох останніх виразів маємо:

.

(4.22)

Зі співвідношень (4.22) виходить, що силовою функцією є така функція координат точки, частинні похідні якої за координатами дорівнюють проекціям сили на відповідні координатні осі.

Робота сили на кінцевій ділянці траєкторії точки М, що визначається дугою

,

(4.23)

де і - значення силової функції в точках і відповідно. З отриманого результата виходить:

при переміщенні точки в потенціальному полі повна робота прикладеної до неї сили дорівнює різниці значень силової функції в кінцевій і початковій точках і не залежить від форми траєкторії, по якій переміщення відбувається.

Сили, що діють на матеріальну точку в потенціальному полі, називаються потенціальними (сили тяжіння, лінійна сила пружності, сила ваги).

Визначимо умови, за якими можна визначити існування потенціальної функції сили . Для цього візьмемо частинні похідні від правих і лівих частин рівнянь (4.22):

і т.д.

За властивостями змішаних частинних похідних:

… і т.д.

Звідсіля виходять умови існування потенціальності силового поля:

.

(4.24)

Приклад: Визначити, чи є потенціальним силове поле, в якому , а - деяка додатна стала.

Згідно з (4.24) маємо:

Очевидно, що в загальному випадку дане силове поле не буде потенціальним, оскільки . Але у випадку, коли і поле виявляється потенціальним.

Потенціальна сила завжди напрямлена по нормалі до поверхні рівня (еквіпотенціальної поверхні) в даній точці. Рівняння поверхні .