
- •Динаміка
- •3.1. Динаміка і її основні задачі
- •3.2. Динаміка матеріальної точки
- •3.2.1. Диференціальні рівняння руху матеріальної точки
- •3.2.2. Дві задачі динаміки матеріальної точки
- •Перша (пряма) задача динаміки точки
- •Друга (обернена) задача динаміки точки
- •3.2.3. Прямолінійні коливання матеріальної точки
- •3.2.3.1. Вільні коливання матеріальної точки
- •3.2.3.2. Згасаючі коливання матеріальної точки
- •Вимушені коливання без урахування опору середовища
- •3.2.3.4. Вимушені коливання при наявності опору
- •Питання для самоконтролю
- •3.3. Загальні відомості про механічну систему
- •3.3.1. Механічна система і сили, що діють на її складові
- •3.3.2. Маса і центр мас системи
- •3.3.3. Моменти інерції
- •Теорема Гюйгенса
- •Обчислення осьових моментів інерції деяких однорідних тіл
- •3.3.4. Диференціальні рівняння руху механічної системи
- •Питання для самоконтролю
- •3.4. Загальні теореми динаміки
- •3.4.1. Кількість руху і теореми про зміну кількості руху матеріальної точки і системи
- •Питання для самоконтролю
- •Теореми про зміну моментів кількості руху матеріальної точки та механічної системи
- •Кінетичний момент твердого тіла відносно осі обертання
- •Теорема моментів
- •Диференціальне рівняння обертання твердого тіла навколо нерухомої осі
- •Обчислення кінетичного момента в деяких випадках руху твердого тіла
- •Питання для самоконтролю
- •3.4.3. Кінетична енергія і робота. Теореми про зміну кінетичної енергії
- •3.4.3.1. Кінетична енергія
- •3.4.3.2. Робота сили
- •3.4.3.3. Теореми про зміну кінетичної енергії
- •3.5 Динаміка плоскопаралельного руху твердого тіла
- •Питання для самоконтролю
- •Кінетостатика і елементи аналітичної механіки
- •4.1. Принцип Даламбера
- •Принцип Даламбера для механічної системи
- •Зведення сил інерції точок твердого тіла до найпростішого виду
- •Поступальний рух твердого тіла
- •Питання для самоконтролю
- •4.2. Принцип можливих переміщень
- •Поняття про можливу роботу
- •4.3. Загальне рівняння динаміки
- •4.4. Рівняння Ланранжа другого роду
- •4.4.1. Силове поле
- •4.4.2. Потенціальна енергія силового поля
- •4.4.3. Закон збереження механічної енергії
- •4.4.4. Узагальнені координати, швидкості і сили
- •4.4.5. Диференціальні рівняння руху механічної системи в узагальнених координатах (рівняння Лагранжа другого роду)
- •Питання для самоконтролю
- •Література
4.1. Принцип Даламбера
Принцип Даламбера дозволяє приводити всі задачі, які відносяться до руху тіл, до більш простої задачі про рівновагу.
Сучасне трактування принципа Даламбера з використанням поняття сили інерції, яке було уведено в механіку на початку ХІХ століття, є фундаментом важливого метода технічної механіки – метода кінетостатики.
Розглянемо матеріальну точку М
масою m, що рухається
з деяким прискоренням
![]() вздовж траєкторії АВ. Припустимо, що
на точку діє система активних сил,
рівнодіючу яких позначимо через
вздовж траєкторії АВ. Припустимо, що
на точку діє система активних сил,
рівнодіючу яких позначимо через
![]() ,
а також реакції в’язей (у випадку якщо
точка є невільною) з рівнодіючою
,
а також реакції в’язей (у випадку якщо
точка є невільною) з рівнодіючою
![]() (рис.4.1).
(рис.4.1).
Т оді,
згідно з рівнянням динаміки для невільної
точки (3.7):
оді,
згідно з рівнянням динаміки для невільної
точки (3.7):
![]() ,
,
або
![]() (4.1)
(4.1)
Позначимо:
![]() .
(4.2)
.
(4.2)
Рис.4.1
Вектор
![]() називають даламберовою силою інерції.
Її можна розглядати як силу, з якою точка
діє на тіла, що надають прискорення
даній точці.
називають даламберовою силою інерції.
Її можна розглядати як силу, з якою точка
діє на тіла, що надають прискорення
даній точці.
Сила інерції матеріальної точки за величиною дорівнює добутку маси точки на модуль її прискорення і має напрям, протилежний напряму прискорення (але не руху).
Таким чином, рівність (4.1) набуває вигляду:
|
|
(4.3) |
Останнє рівняння і виражає принцип Даламбера:
для невільної матеріальної точки в кожний момент часу сума активних сил, що прикладені до точки, реакцій її в’язей і сили інерції дорівнює нулю.
При координатному способі задання руху
в системі відліку
![]() векторне рівняння (4.3) переходить в
систему скалярних рівнянь:
векторне рівняння (4.3) переходить в
систему скалярних рівнянь:
|
|
(4.4) |
Якщо ж рух точки задано натуральним способом, то будемо мати систему таких рівнянь:
|
|
(4.5) |
В рівняннях (4.4) і (4.5)
![]() ;
;
![]() ;
;
![]() ;
;
![]() - тангенціальна складова сили інерції;
- тангенціальна складова сили інерції;
 - нормальна (відцентрова) сила інерції;
- нормальна (відцентрова) сила інерції;
![]() (рис.4.2).
(рис.4.2).

Рис.4.2
Принцип Даламбера для механічної системи
Нехай у довільній точці
![]() масою
масою
![]() системи, що складається з
системи, що складається з
![]() матеріальних точок, прикладені активна
сила
матеріальних точок, прикладені активна
сила
![]() і реакція в’язі
і реакція в’язі
![]() .
Тоді для
.
Тоді для
![]() ї
точки рівняння кінетостатики запишеться
так:
ї
точки рівняння кінетостатики запишеться
так:
|
|
(4.6) |
Підсумуємо рівняння по всіх точках механічної системи і дістанемо:
|
|
(4.7) |
Позначивши головні вектори активних
сил, реакцій в’язей і сил інерції
відповідно через
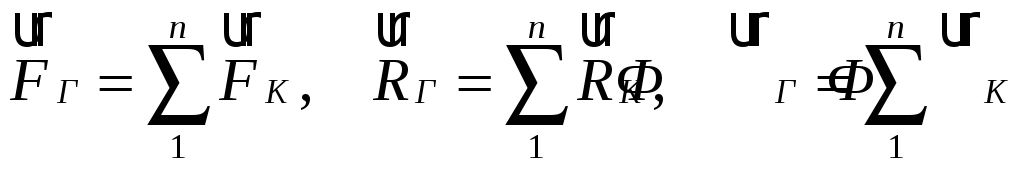 ,
вираз (4.7) запишемо у вигляді:
,
вираз (4.7) запишемо у вигляді:
|
|
(4.8) |
Припустимо, що положення
![]() ї
точки даної системи в декартових
координатах
ї
точки даної системи в декартових
координатах
![]() визначається радіусом-вектором
визначається радіусом-вектором
![]() .
Помножимо його векторно на сили, які
входять до рівняння (4.6), і визначимо їх
моменти відносно центра О:
.
Помножимо його векторно на сили, які
входять до рівняння (4.6), і визначимо їх
моменти відносно центра О:
|
|
|
або:
|
|
|
Підсумуємо останні співвідношення по всіх точках системи:
|
|
(4.9) |
Якщо використати поняття головних моментів цих сил, то останнє рівняння набуває такої форми:
|
|
(4.10) |
Рівняння (4.8) і (4.10) виражають принцип Даламбера для механічної системи: в кожний момент часу векторні суми головних векторів активних сил, реакцій в’язей і сил інерції і головних моментів цих же сил відносно обраного центра дорівнюють нулю.
Отриманим векторним рівнянням (4.7) і (4.9), чи (4.8) і (4.10) відповідають шість алгебраїчних рівнянь в координатній формі:
|
|
(4.11) |
Оскільки головний вектор і головний момент внутрішніх сил дорівнюють нулю, то в рівняннях (4.11) внутрішні сили відсутні.




 .
.