
- •Динаміка
- •3.1. Динаміка і її основні задачі
- •3.2. Динаміка матеріальної точки
- •3.2.1. Диференціальні рівняння руху матеріальної точки
- •3.2.2. Дві задачі динаміки матеріальної точки
- •Перша (пряма) задача динаміки точки
- •Друга (обернена) задача динаміки точки
- •3.2.3. Прямолінійні коливання матеріальної точки
- •3.2.3.1. Вільні коливання матеріальної точки
- •3.2.3.2. Згасаючі коливання матеріальної точки
- •Вимушені коливання без урахування опору середовища
- •3.2.3.4. Вимушені коливання при наявності опору
- •Питання для самоконтролю
- •3.3. Загальні відомості про механічну систему
- •3.3.1. Механічна система і сили, що діють на її складові
- •3.3.2. Маса і центр мас системи
- •3.3.3. Моменти інерції
- •Теорема Гюйгенса
- •Обчислення осьових моментів інерції деяких однорідних тіл
- •3.3.4. Диференціальні рівняння руху механічної системи
- •Питання для самоконтролю
- •3.4. Загальні теореми динаміки
- •3.4.1. Кількість руху і теореми про зміну кількості руху матеріальної точки і системи
- •Питання для самоконтролю
- •Теореми про зміну моментів кількості руху матеріальної точки та механічної системи
- •Кінетичний момент твердого тіла відносно осі обертання
- •Теорема моментів
- •Диференціальне рівняння обертання твердого тіла навколо нерухомої осі
- •Обчислення кінетичного момента в деяких випадках руху твердого тіла
- •Питання для самоконтролю
- •3.4.3. Кінетична енергія і робота. Теореми про зміну кінетичної енергії
- •3.4.3.1. Кінетична енергія
- •3.4.3.2. Робота сили
- •3.4.3.3. Теореми про зміну кінетичної енергії
- •3.5 Динаміка плоскопаралельного руху твердого тіла
- •Питання для самоконтролю
- •Кінетостатика і елементи аналітичної механіки
- •4.1. Принцип Даламбера
- •Принцип Даламбера для механічної системи
- •Зведення сил інерції точок твердого тіла до найпростішого виду
- •Поступальний рух твердого тіла
- •Питання для самоконтролю
- •4.2. Принцип можливих переміщень
- •Поняття про можливу роботу
- •4.3. Загальне рівняння динаміки
- •4.4. Рівняння Ланранжа другого роду
- •4.4.1. Силове поле
- •4.4.2. Потенціальна енергія силового поля
- •4.4.3. Закон збереження механічної енергії
- •4.4.4. Узагальнені координати, швидкості і сили
- •4.4.5. Диференціальні рівняння руху механічної системи в узагальнених координатах (рівняння Лагранжа другого роду)
- •Питання для самоконтролю
- •Література
3.4.3. Кінетична енергія і робота. Теореми про зміну кінетичної енергії
Кінетична енергія також є мірою механічного руху матеріальних об’єктів, але на відміну від кількості руху і кінетичного момента, які використовують для характеристики відповідно поступального і обертального рухів, вона існує при будь-якому русі матеріальної точки чи механічної системи.
В свою чергу, кінетична енергія тісно пов’язана з поняттям роботи сили.
3.4.3.1. Кінетична енергія
Кінетичною енергією матеріальної точки називається скалярна величина, що дорівнює половині добутку її маси на квадрат швидкості точки:
|
|
(3.89) |
З визначення кінетичної енергії виходить,
що вона є скалярною додатною
величиною; одиниця її вимірювання
![]() або
або
![]() .
.
Кінетичною енергією механічної системи називають суму кінетичних енергій всіх точок цієї системи:
|
|
(3.90) |
При поступальному русі твердого тіла
миттєві швидкості всіх його точок
однакові і дорівнюють швидкості
![]() центра мас тіла. Тому формула (3.90) набуває
вигляду:
центра мас тіла. Тому формула (3.90) набуває
вигляду:
|
|
(3.91) |
де
![]() - маса тіла.
- маса тіла.
При обертанні тіла навколо нерухомої
осі (наприклад, осі
![]() )
лінійна швидкість
)
лінійна швидкість
![]() -ї
точки тіла
-ї
точки тіла
![]() ,
де
,
де
![]() - відстань точки до осі обертання. Тоді:
- відстань точки до осі обертання. Тоді:
|
|
(3.92) |
оскільки
 - момент інерції
- момент інерції
![]() тіла навколо осі обертання.
тіла навколо осі обертання.
Плоскопаралельний рух тіла можна розглядати як миттєвообертальний навколо осі, що проходить через МЦШ Р. Отже, на підставі (3.92), отримаємо:
|
|
(3.93) |
де
![]() - момент інерції тіла навколо осі, що
проходить через МЦШ.
- момент інерції тіла навколо осі, що
проходить через МЦШ.
Але користування формулою (3.93) не завжди
зручно, бо положення миттєвого центра
швидкостей при русі тіла змінюється і
величина
![]() також буде змінною.
також буде змінною.
За теоремою Гюйгенса:
![]() ,
,
де:
![]() - момент інерції тіла відносно осі, яка
проходить через центр мас С тіла
паралельно до миттєвої осі обертання.
Крім того, якщо швидкість центра мас
тіла
- момент інерції тіла відносно осі, яка
проходить через центр мас С тіла
паралельно до миттєвої осі обертання.
Крім того, якщо швидкість центра мас
тіла
![]() виразити через добуток кутової швидкості
тіла на відстань центра мас до МЦШ -
виразити через добуток кутової швидкості
тіла на відстань центра мас до МЦШ -
![]() ,
то (3.93) набуває вигляду:
,
то (3.93) набуває вигляду:
|
|
(3.94) |
Тобто, кінетична енергія тіла при плоскопаралельному русі складається з енергії поступального руху зі швидкістю центра мас і енергії обертального руху навколо центра мас.
3.4.3.2. Робота сили
Для характеристики ефекту дії сили на матеріальний об’єкт при його переміщенні користуються поняттям роботи сили.
Розглянемо рух матеріальної точки М
під дією сили
![]() вздовж криволінійної траєкторії (рис.
3.18). За нескінченно малий проміжок часу
вздовж криволінійної траєкторії (рис.
3.18). За нескінченно малий проміжок часу
![]() радіус-вектор точки
радіус-вектор точки
![]() отримає приріст
отримає приріст
![]() ,
який називають елементарним переміщенням
точки
,
який називають елементарним переміщенням
точки
![]() .
.


Рис. 3.18
Скалярний добуток вектора сили
![]() на елементарне переміщення точки
називають елементарною роботою
на елементарне переміщення точки
називають елементарною роботою
![]() сили:
сили:
|
|
(3.95) |
Робота сили на будь-якому скінченому
переміщенні
![]() точки її прикладання (рис.3.18) визначається
як границя інтегральної суми відповідних
елементарних робіт:
точки її прикладання (рис.3.18) визначається
як границя інтегральної суми відповідних
елементарних робіт:
|
|
(3.96) |
В системі СІ одиницею роботи є Джоуль:
![]() .
.
Якщо вектор сили
![]() і вектор елементарного переміщення
і вектор елементарного переміщення
![]() точки розкласти по координатних осях:
точки розкласти по координатних осях:
![]() ,
,
![]() ,
то отримаємо аналітичні вирази роботи
сили:
,
то отримаємо аналітичні вирази роботи
сили:
|
|
(3.97) |
|
і
|
(3.98) |
Останні дві формули визначають роботу сили при координатному способі завдання руху.
Скористаємось співвідношенням для
визначення проекції швидкості точки в
системі координат
![]() :
:
![]() ,
з яких виходить, що
,
з яких виходить, що
![]() .
Тоді:
.
Тоді:
|
|
(3.99) |
|
|
(3.100) |
В натуральній системі координат
![]() елементарне переміщення
елементарне переміщення
![]() ,
де
,
де
![]() -орт
дотичної;
-орт
дотичної;
![]() - диференціал дуги траєкторії точки,
тому елементарна робота сили:
- диференціал дуги траєкторії точки,
тому елементарна робота сили:
|
|
(3.101) |
Відповідно, повна робота сили:
|
|
(3.102) |
В останній формулі
![]() - дугові координати, які відповідають
положенням
- дугові координати, які відповідають
положенням
![]() матеріальної точки на її траєкторії
(рис.3.18).
матеріальної точки на її траєкторії
(рис.3.18).
В інженерній практиці користуються поняттям потужності, якою оцінюють роботу сили за одиницю часу:
![]() .
.
З урахуванням рівняння (3.99), отримаємо:
|
|
(3.103) |
Тобто, потужністю сили називається величина, що дорівнює скалярному добутку вектора сили на вектор швидкості точки її прикладання.
Розглянемо приклади обчислення роботи деяких сил.
-
Р
 обота
сили тяжіння матеріальної точки.
Припустимо, що точка М, на яку діє
сила ваги
обота
сили тяжіння матеріальної точки.
Припустимо, що точка М, на яку діє
сила ваги
 ,
переміщується з положення
,
переміщується з положення
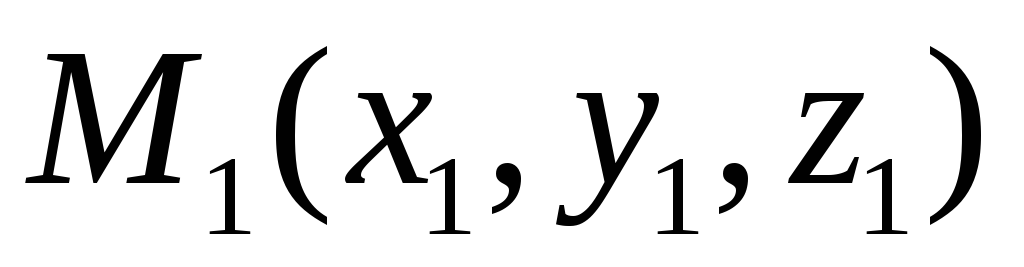 в системі координат
в системі координат
 в положення
в положення
 ,
причому вісь
,
причому вісь
 напрямлена вертикально вверх (рис.3.19).
напрямлена вертикально вверх (рис.3.19).
Рис.3.19
В цьому випадку
![]() і згідно з формулою (3.98)
і згідно з формулою (3.98)
|
|
(3.104) |
Позначимо вертикальне переміщення
точки через
![]() .
Тоді при
.
Тоді при
![]()
![]() буде додатною величиною, а при
буде додатною величиною, а при
![]() - від’ємною. З урахуванням цього можна
записати, що
- від’ємною. З урахуванням цього можна
записати, що
|
|
(3.105) |
2. Робота сили тяжіння механічної
системи. Для системи, що складається
з
![]() матеріальних точок, робота сили ваги
матеріальних точок, робота сили ваги
![]() ї
точки масою
ї
точки масою
![]() :
:
![]() .
.
Для механічної системи в цілому сумарна робота сил тяжіння:
|
|
(3.106) |
де
![]() - маса всієї системи;
- маса всієї системи;
![]() початкова
і кінцева висотні координати центра
мас системи.
початкова
і кінцева висотні координати центра
мас системи.
Якщо позначити
![]() ,
то:
,
то:
|
|
(3.107) |
де
![]() - зміна висотного положення центра мас
системи.
З наведених формул виходить,
що робота сил тяжіння не залежить від
форми траєкторії, вздовж якої рухається
матеріальний об’єкт, а визначається
тільки різницею його висотного положення
на початку і в кінці руху.
- зміна висотного положення центра мас
системи.
З наведених формул виходить,
що робота сил тяжіння не залежить від
форми траєкторії, вздовж якої рухається
матеріальний об’єкт, а визначається
тільки різницею його висотного положення
на початку і в кінці руху.
-
Робота сили пружності. В загальному випадку лінійна сила пружності відповідає закону Гука:
![]() ,
,
де
![]() -
радіус-вектор, яким визначається відстань
точки від положення рівноваги; с-
коефіцієнт жорсткості. Якщо брати за
положення рівноваги початок системи
координат
-
радіус-вектор, яким визначається відстань
точки від положення рівноваги; с-
коефіцієнт жорсткості. Якщо брати за
положення рівноваги початок системи
координат
![]() (рис. 3.20), то
(рис. 3.20), то
![]() ;
;
![]() ;
;
![]() .
.

Рис. 3.20
Роботу сили
![]() на переміщенні від положення
на переміщенні від положення
![]() до положення
до положення
![]() визначимо за формулою (3.98):
визначимо за формулою (3.98):
 .
.
Тут враховано, що
![]() і
і
![]() .
.
Проінтегрувавши, отримаємо:
|
|
(3.108) |
Для пружини з початковою деформацією
![]() і кінцевою
і кінцевою
![]() ,
формула набуває вигляду:
,
формула набуває вигляду:
|
|
(3.109) |
-
Робота сили, прикладеної до твердого тіла що обертається навколо осі. Розглянемо випадок, коли сила
 прикладена до деякої точки К твердого
тіла, яке обертається навколо нерухомої
осі
прикладена до деякої точки К твердого
тіла, яке обертається навколо нерухомої
осі
 (рис.3.21).
(рис.3.21).
z![]()


Рис.3.21
Розкладемо цю силу по осях натурального
тригранника
![]() .
Так як складові
.
Так як складові
![]() і
і
![]() перпендикулярні до переміщення точки
К їх прикладання, то робота цих
складових на елементарному переміщенні
перпендикулярні до переміщення точки
К їх прикладання, то робота цих
складових на елементарному переміщенні
![]() дорівнює нулю. Отже, виходить, що:
дорівнює нулю. Отже, виходить, що:
![]() .
.
Тут
![]() - відстань точки К від осі обертання;
- відстань точки К від осі обертання;
![]() - елементарний кут повороту. Але
- елементарний кут повороту. Але
![]() ,
тому
,
тому
|
|
(3.110) |
Таким чином, елементарна робота сили, прикладеної до будь-якої точки твердого тіла, що обертається навколо нерухомої осі, дорівнює добутку момента сили відносно осі обертання на диференціал кута повороту тіла.
Повна робота сили
![]() при повороті тіла на скінчений кут:
при повороті тіла на скінчений кут:
|
|
(3.111) |
В частинному випадку, якщо
![]() ,
отримаємо:
,
отримаємо:
|
|
(3.112) |
З рівняння (3.110) виходить співвідношення для визначення потужності момента сили:
|
|
(3.113) |
-
Робота сил тертя, прикладених до тіла, яке котиться.
Хай на коток радіуса
![]() і вагою
і вагою
![]() ,
що котиться без ковзання по деякій
площині, діє сила тертя ковзання
,
що котиться без ковзання по деякій
площині, діє сила тертя ковзання
![]() (рис.3.22).
(рис.3.22).

Рис.3.22
Ця сила прикладена в точці
![]() контакту котка і площини. Згідно із
визначенням елементарна робота сили
контакту котка і площини. Згідно із
визначенням елементарна робота сили
![]()
![]() .
Але в кожний момент часу точка В
співпадає з МЦШ котка і тому
.
Але в кожний момент часу точка В
співпадає з МЦШ котка і тому
![]() .
Так як
.
Так як
![]() ,
то
,
то
![]() .
.
Таким чином, при коченні без ковзання робота сили тертя ковзання на будь-якому переміщенні тіла дорівнює нулю.
Опір коченню створює пара сил
![]() ,
момент якої
,
момент якої
![]() ,
де
,
де
![]() -
коефіцієнт тертя кочення. Тоді відповідно
до формули (3.110):
-
коефіцієнт тертя кочення. Тоді відповідно
до формули (3.110):
|
|
(3.114) |
де
![]() - елементарне переміщення центра мас С
котка, що дорівнює
- елементарне переміщення центра мас С
котка, що дорівнює
![]() .
.
Якщо нормальна реакція
![]() ,
то робота момента сил опору коченню
,
то робота момента сил опору коченню
|
|
(3.115) |

 .
. ,
, .
.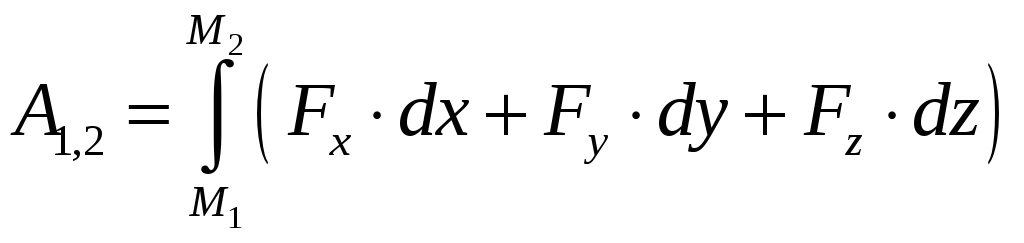 .
. .
. .
. .
. ,
,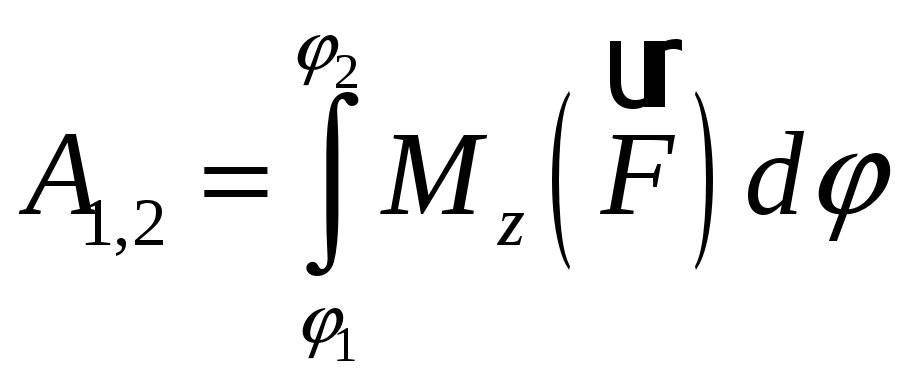 .
.