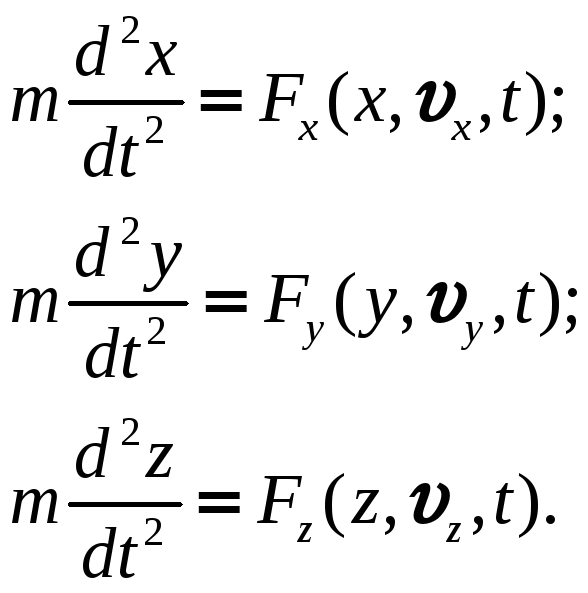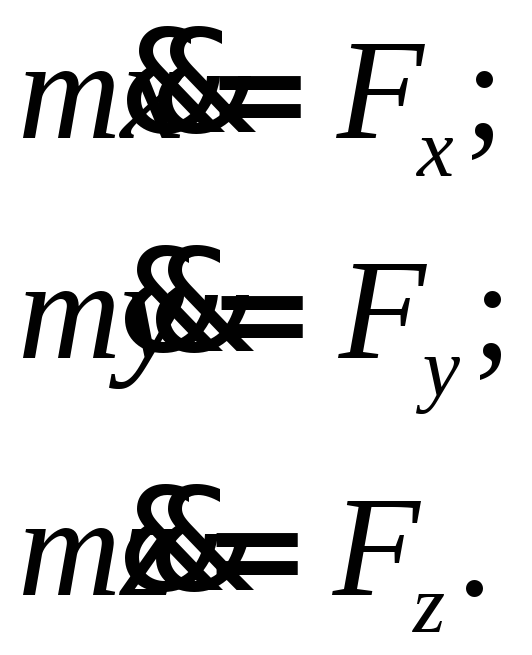- •Динаміка
- •3.1. Динаміка і її основні задачі
- •3.2. Динаміка матеріальної точки
- •3.2.1. Диференціальні рівняння руху матеріальної точки
- •3.2.2. Дві задачі динаміки матеріальної точки
- •Перша (пряма) задача динаміки точки
- •Друга (обернена) задача динаміки точки
- •3.2.3. Прямолінійні коливання матеріальної точки
- •3.2.3.1. Вільні коливання матеріальної точки
- •3.2.3.2. Згасаючі коливання матеріальної точки
- •Вимушені коливання без урахування опору середовища
- •3.2.3.4. Вимушені коливання при наявності опору
- •Питання для самоконтролю
- •3.3. Загальні відомості про механічну систему
- •3.3.1. Механічна система і сили, що діють на її складові
- •3.3.2. Маса і центр мас системи
- •3.3.3. Моменти інерції
- •Теорема Гюйгенса
- •Обчислення осьових моментів інерції деяких однорідних тіл
- •3.3.4. Диференціальні рівняння руху механічної системи
- •Питання для самоконтролю
- •3.4. Загальні теореми динаміки
- •3.4.1. Кількість руху і теореми про зміну кількості руху матеріальної точки і системи
- •Питання для самоконтролю
- •Теореми про зміну моментів кількості руху матеріальної точки та механічної системи
- •Кінетичний момент твердого тіла відносно осі обертання
- •Теорема моментів
- •Диференціальне рівняння обертання твердого тіла навколо нерухомої осі
- •Обчислення кінетичного момента в деяких випадках руху твердого тіла
- •Питання для самоконтролю
- •3.4.3. Кінетична енергія і робота. Теореми про зміну кінетичної енергії
- •3.4.3.1. Кінетична енергія
- •3.4.3.2. Робота сили
- •3.4.3.3. Теореми про зміну кінетичної енергії
- •3.5 Динаміка плоскопаралельного руху твердого тіла
- •Питання для самоконтролю
- •Кінетостатика і елементи аналітичної механіки
- •4.1. Принцип Даламбера
- •Принцип Даламбера для механічної системи
- •Зведення сил інерції точок твердого тіла до найпростішого виду
- •Поступальний рух твердого тіла
- •Питання для самоконтролю
- •4.2. Принцип можливих переміщень
- •Поняття про можливу роботу
- •4.3. Загальне рівняння динаміки
- •4.4. Рівняння Ланранжа другого роду
- •4.4.1. Силове поле
- •4.4.2. Потенціальна енергія силового поля
- •4.4.3. Закон збереження механічної енергії
- •4.4.4. Узагальнені координати, швидкості і сили
- •4.4.5. Диференціальні рівняння руху механічної системи в узагальнених координатах (рівняння Лагранжа другого роду)
- •Питання для самоконтролю
- •Література
-
Динаміка
3.1. Динаміка і її основні задачі
Два попередні розділи курсу механіки – статика і кінематика – по суті мало зв’язані між собою. Кожному з них відповідає своє окреме коло понять, задач і методів їх розв’язання. У статиці розглядаються задачі на рівновагу, а також задачі еквівалентних перетворень систем сил; при таких перетвореннях навіть не постає питання про те, який рух тіла викликають прикладені сили. У кінематиці вивчається рух «сам по собі» без зв’язку з тими силами, під дією яких він відбувається.
Динаміка - це основний розділ теоретичної механіки, де узагальнюються положення і висновки, отримані в статиці і кінематиці; тобто динаміка вивчає механічний рух матеріальних об’єктів, що виникає під дією сил, прикладених до цих об’єктів.
Саме у динаміці ставляться і розв’язуються дві основні задачі механіки: а) за відомим законом руху матеріального об’єкта потрібно визначити сили, які цей рух викликають (перша або пряма задача); б) за відомими силами, що діють на матеріальний об’єкт, потрібно знайти закон його руху (друга або обернена задача).
Звичайно динаміку в залежності від конкретного поняття матеріального об’єкта поділяють на три частини: динаміку матеріальної точки, динаміку системи матеріальних точок і динаміку твердого тіла.
-
3.2. Динаміка матеріальної точки
Фундаментом класичної динаміки є другий закон Ньютона, який називають основним законом динаміки. Нагадаємо, що математична форма запису цього закону для матеріальної точки дається рівнянням:
|
|
|
де:
![]() - маса точки;
- маса точки;
![]() - швидкість точки;
- швидкість точки;
![]() - рівнодіюча всіх сил, прикладених до
точки.
- рівнодіюча всіх сил, прикладених до
точки.
В тих випадках, коли можна прийняти умову про сталість маси, основне диференціальне рівняння динаміки точки набуває вигляду:
|
|
(3.1) |
(![]() - абсолютне прискорення точки).
- абсолютне прискорення точки).
3.2.1. Диференціальні рівняння руху матеріальної точки
Як відомо, положення матеріальної точки
в інерціальній системі відліку
визначається її радіусом-вектором
![]() .
Сила
.
Сила
![]() ,
що діє на точку, може залежати від
положення точки, тобто від радіуса-вектора
,
що діє на точку, може залежати від
положення точки, тобто від радіуса-вектора
![]() (наприклад, сила тяжіння), швидкості
(наприклад, сила тяжіння), швидкості
![]() точки (наприклад, сила опору) і часу
точки (наприклад, сила опору) і часу
![]() .
Отже, в загальному випадку основне
диференціальне рівняння (3.1) можна
записати в такій формі:
.
Отже, в загальному випадку основне
диференціальне рівняння (3.1) можна
записати в такій формі:
|
|
(3.2) |
Це рівняння називається диференціальним рівнянням руху матеріальної точки у векторній формі.
Диференціальне рівняння у векторній формі еквівалентне певній системі скалярних (алгебраїчних) рівнянь. В залежності від вибору координатних осей, на які проектується основне рівняння динаміки (3.1), отримують різні форми скалярних диференціальних рівнянь руху матеріальної точки.
Так, якщо спроектувати рівняння (3.2) на
координатні осі
![]() декартової нерухомої системи координат,
то будемо мати:
декартової нерухомої системи координат,
то будемо мати:
|
|
(3.3) |
У спрощеній формі запису ця система рівнянь набуває вигляду:
|
|
(3.4) |

Рис.3.1
При використовуванні природної системи координат для опису руху матеріальної точки потрібно спроектувати основне диференціальне рівняння динаміки (3.2) на осі природного тригранника (рис.3.1); в результаті отримаємо співвідношення:
|
|
(3.5) |
де
![]() - проекції рівнодіючої сил на дотичну,
головну нормаль і бінормаль.
- проекції рівнодіючої сил на дотичну,
головну нормаль і бінормаль.
Якщо згадати відомі з кінематики вирази
для проекцій
![]() повного прискорення точки на ті ж
напрями, то отримаємо:
повного прискорення точки на ті ж
напрями, то отримаємо:
|
або
|
(3.6) |
Основний закон динаміки і, відповідно, його математичні вирази, наведені вище, сформульовані для вільної матеріальної точки. Якщо на точку накладено певні в’язі, тобто вона є невільною, то на підставі принципу звільнення від в’язей до заданих (активних) сил, що діють на точку, потрібно додати відповідні сили реакції і розглядати матеріальну точку як вільну. Тоді основне рівняння динаміки буде мати вигляд:
|
|
(3.7) |
а алгебраїчні диференціальні рівняння руху точки в проекціях на осі декартової системи координат і на осі природного тригранника наберуть такої форми:
|
|
(3.8) |
і
|
|
(3.9) |

 або
або