
- •2. Кінематика точки і твердого тіла
- •2.1. Способи задання руху точки
- •2.1.1. Векторний спосіб
- •2.1.2. Координатний спосіб
- •2.1.3. Природний спосіб
- •2.2. Швидкість і прискорення точки
- •2.2.1. Векторний спосіб визначення швидкості і прискорення точки
- •2.2.2. Визначення швидкості і прискорення точки в декартовій системі координат
- •2.2.3. Визначення швидкості і прискорення при природному способі задання руху точки
- •Питання для самоконтролю
- •2.3. Кінематика твердого тіла
- •2.3.1. Поступальний рух твердого тіла
- •2.3.2. Обертальний рух твердого тіла навколо нерухомої осі
- •Розподіл швидкостей і прискорень точок тіла при обертальному русі
- •2.3.3. Перетворення найпростіших рухів твердого тіла
- •Питання для самоконтролю
- •2.3.4. Плоскопаралельний рух твердого тіла
- •2.3.4.1. Рівняння і характеристики плоского руху
- •2.3.4.2. Визначення швидкостей точок тіла при плоскопаралельному русі
- •2.3.4.3. Миттєвий центр швидкостей
- •Способи визначення положення мцш
- •2.3.4.4. Прискорення точок при плоскопаралельному русі твердого тіла
- •2.3.4.5. Миттєвий центр прискорень
- •Способи визначення положення мцп
- •Частинні випадки знаходження мцп
- •Питання для самоконтролю
- •2.4. Складання рухів точки і твердого тіла
- •Складний рух точки
- •2.4.1.1. Складання швидкостей
- •2.4.1.2. Додавання прискорень в складному русі
- •Питання для самоконтролю
- •Додавання двох обертальних рухів навколо паралельних осей
Питання для самоконтролю
-
Яка залежність існує між проекціями швидкостей двох точок твердого тіла на пряму, що з’єднує ці точки?
-
Який рух тіла називають поступальним?
-
Чим відрізняється миттєво-поступальний рух від поступального руху тіла?
-
Чи можуть траєкторії точок тіла при його поступальному русі бути колами? Якщо так, то наведіть приклади.
-
Перерахуйте основні властивості поступального руху твердого тіла.
-
Чи можна звести кінематику поступального руху тіла до кінематики точки? Відповідь обґрунтуйте.
-
Кабінка колеса оглядання в процесі свого руху залишається завжди вертикальною. Які точки кабінки мають більше прискорення: точки підлоги чи точки стелі?
-
Який рух твердого тіла називають обертанням навколо нерухомої осі? Що являють собою траєкторії окремих точок при такому русі?
-
Яким рівнянням задається закон обертального руху тіла навколо нерухомої осі?
-
За якими формулами визначаються модулі кутової швидкості і кутового прискорення твердого тіла, що обертається?
-
Як напрямлені вектори кутової швидкості і кутового прискорення при обертанні тіла навколо нерухомої осі?
-
Наведіть формули для визначення величин швидкостей і прискорень окремих точок твердого тіла, яке обертається навколо нерухомої осі.
-
У скільки разів прискорення точки А диска більше прискорення його точки В, якщо відстань точки А від осі обертання диска удвоє більше відстані від осі точки В?
-
При яких умовах напрям прискорення точки при обертанні тіла складає з відрізком, що з’єднує цю точку з центром її траєкторії, кути 00, 450, 900?
-
Визначте геометричні місця точок твердого тіла, що обертається навколо нерухомої осі, для яких прискорення:
а) рівні за модулем;
б) співпадають за напрямом;
в) рівні за модулем і співпадають за напрямом (векторно рівні).
-
Дві шестерні радіусами
 і
і
 знаходяться в зачепленні і обертаються
рівномірно. У якої шестерні прискорення
точки зачеплення більше? У скільки
разів?
знаходяться в зачепленні і обертаються
рівномірно. У якої шестерні прискорення
точки зачеплення більше? У скільки
разів? -
За якою формулою можна перейти при обчисленні кутової швидкості від частоти обертання «
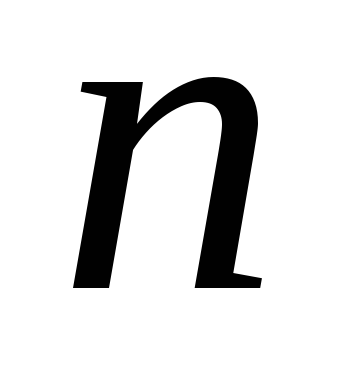 за хвилину» до розмірності «радіан за
секунду»?
за хвилину» до розмірності «радіан за
секунду»?
2.3.4. Плоскопаралельний рух твердого тіла
Плоскопаралельним або плоским рухом твердого тіла називається такий рух, при якому всі точки тіла рухаються паралельно певній нерухомій в даній системі відліку площині.
Плоский рух твердого тіла широко розповсюджений в техніці, оскільки окремі ланки значної кількості механізмів і машин здійснюють тільки плоский рух (кривошипно-шатунні, кулісні, епіціклічні механізми).
2.3.4.1. Рівняння і характеристики плоского руху
З визначення
плоскопаралельного руху виходить, що
він повністю характеризується рухом
плоскої фігури, утвореної перерізом
тіла площиною, паралельною певній
нерухомій площині. В подальшому будемо
вважати, що рух плоскої фігури відбувається
в площині рисунка і, відповідно, рисунок
є натуральним зображенням фігури. В
свою чергу, положення плосокї фігури в
координатній площині, наприклад,
![]() ,
яка обрана за базову, визначається
положенням будь-якого відрізка
,
яка обрана за базову, визначається
положенням будь-якого відрізка
![]() цієї фігури (рис.2.14). З аналітичної
геометрії відомо, що положення відрізка
в площині його руху можна однозначно
визначити координатами довільної точки
відрізка (наприклад, координатами
цієї фігури (рис.2.14). З аналітичної
геометрії відомо, що положення відрізка
в площині його руху можна однозначно
визначити координатами довільної точки
відрізка (наприклад, координатами
![]() ,
,
![]() точки А)
і кутом
точки А)
і кутом
![]() між відрізком і однією з координатних
осей (наприклад, віссю
між відрізком і однією з координатних
осей (наприклад, віссю
![]() ).
Точку, обрану для визначення положення
плоскої фігури, називають полюсом.
).
Точку, обрану для визначення положення
плоскої фігури, називають полюсом.

Рис. 2.14
Таким чином, закон
руху плоскої фігури в її площині, а отже,
і плоско-паралельного руху тіла в цілому,
відносно обраної системи координат
![]() описується трьома рівняннями:
описується трьома рівняннями:
|
|
(2.36) |
Аналіз залежностей (2.36) дає можливість зробити висновок, що плоско-паралельний рух тіла є сукупністю двох простих рухів: поступального, при якому всі точки тіла рухаються так само, як і полюс (точка А), і обертального – навколо осі, що проходить через полюс перпендикулярно до площини руху тіла.
Основними
кінематичними характеристиками
плоскопаралельного руху є швидкість і
прискорення полюса (в нашому випадку
![]() ,
,
![]() ),
а також кутова швидкість
),
а також кутова швидкість
![]() і кутове прискорення
і кутове прискорення
![]() тіла.
тіла.
Взагалі за полюс
можна вибрати будь-яку точку тіла.
Причому, при зміні точки, що вибирається
за полюс, характеристики поступальної
частини руху змінюється, а характеристики
обертальної частини руху
![]() і
і
![]() залишаються незмінними.
залишаються незмінними.
