
- •Статика твердого тіла
- •Аксіоми статики вільного твердого тіла
- •Дві найпростіші теореми статики
- •Вільні і невільні тіла. В’язі і їх реакції
- •Класифікація сил. Метод перерізів
- •Системи збіжних сил і умови їх рівноваги
- •Зведення до рівнодіючої і геометричні умови рівноваги збіжних сил
- •Аналітичні умови рівноваги систем збіжних сил
- •Теорема Варіньона (терема про момент рівнодіючої збіжної системи сил)
- •Питання для самоконтролю
- •Довільна просторова система сил і умови її рівноваги
- •Теорема про паралельний перенос сили
- •Основна теорема статики (теорема Пуансо)
- •1.8.3. Залежність головного вектора і головного момента від вибору центра зведення
- •1.8.4. Умови рівноваги довільної просторової системи сил
- •1.9. Окремі випадки рівноваги систем сил
- •1.9.1. Умови рівноваги просторової системи паралельних сил
- •1.9.2. Умови рівноваги плоскої системи сил
- •1.9.3. Умови рівноваги плоскої системи паралельних сил
- •Питання для самоконтролю
- •1.10. Тертя
- •1.10.1. Зчеплення і тертя ковзання
- •1.10.2. Рівновага гнучкої нитки на негладкій циліндричній поверхні
- •1.10.3. Тертя кочення
- •1.11. Центр паралельних сил. Центр ваги тіла
- •1.11.1. Рівнодіюча систем двох паралельних сил, які не утворюють пару
- •1.11.2. Центр паралельних сил
- •1.11.3 Центр ваги твердого тіла
- •Питання для самоконтролю
1.8.3. Залежність головного вектора і головного момента від вибору центра зведення
Припустимо, що задану довільну систему
сил
![]() ,
яка була зведена до центра О і мала
головний вектор
,
яка була зведена до центра О і мала
головний вектор
![]() і головний момент
і головний момент
![]() ,
потрібно звести до іншого центра,
наприклад, О1 (рис.1.16).
,
потрібно звести до іншого центра,
наприклад, О1 (рис.1.16).
Згідно з теоремою про
паралельний перенос сили
головний вектор заданої
системи сил залишиться
незмінним, тобто
![]() .
Але при цьому з’явиться приєднана пара
(
.
Але при цьому з’явиться приєднана пара
(![]() )
з моментом, рівним моменту головного
вектора
)
з моментом, рівним моменту головного
вектора
![]() відносно нового центра зведення:
відносно нового центра зведення:
-
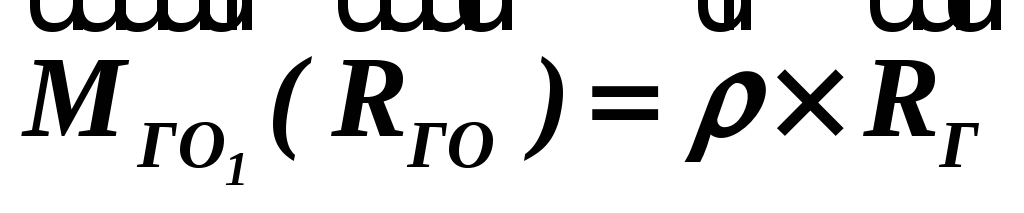
(1.13)
Тоді головний момент заданої системи сил відносно нового центра буде таким:
-
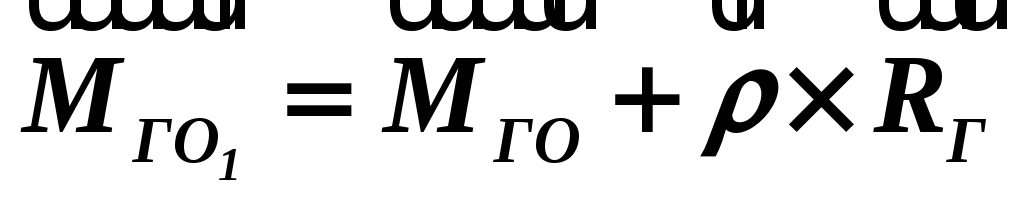
(1.14)
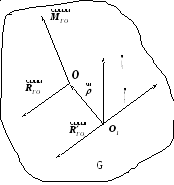
Рис.1.16
Висновок: при зміні центра зведення головний вектор системи сил не змінюється, а головний момент цієї системи змінюється на величину, що дорівнює моменту головного вектора, прикладеного в старому центрі, відносно нового центра зведення.
1.8.4. Умови рівноваги довільної просторової системи сил
З теореми про зведення довільної системи сил до сили і пари сил можна отримати умови рівноваги просторової системи сил, які діють на тверде тіло. Очевидно, що у випадку, коли система сил знаходиться в рівновазі, то в рівновазі знаходиться і еквівалентна їй система, яка складається з сили і пари сил. Тому для рівноваги довільної системи сил, прикладених до твердого тіла, необхідно й досить, щоб головний вектор і головний момент цієї системи відносно будь-якого центра зведення були рівними нулю. Тобто:
-
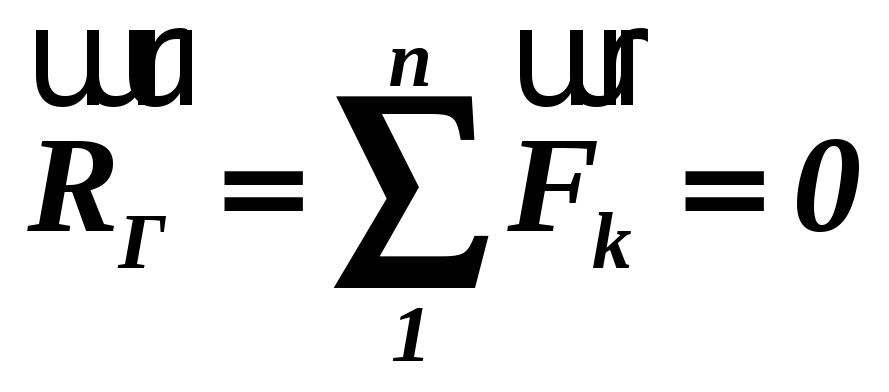 ,
,
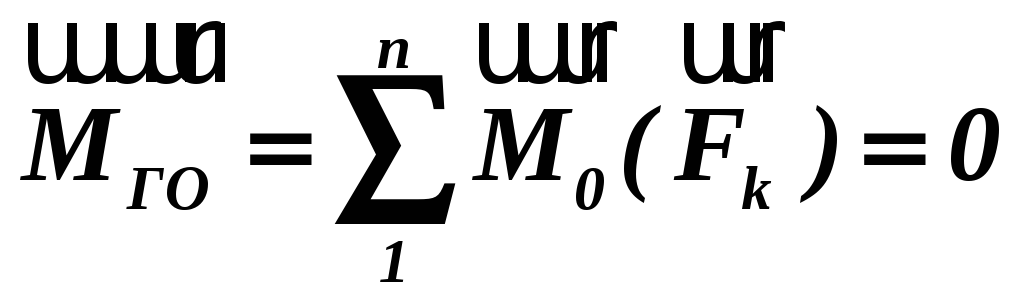
(1.15)
З векторних умов рівноваги просторової системи сил виходять алгебраїчні умови рівноваги такої системи сил:
-
1
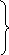 .
.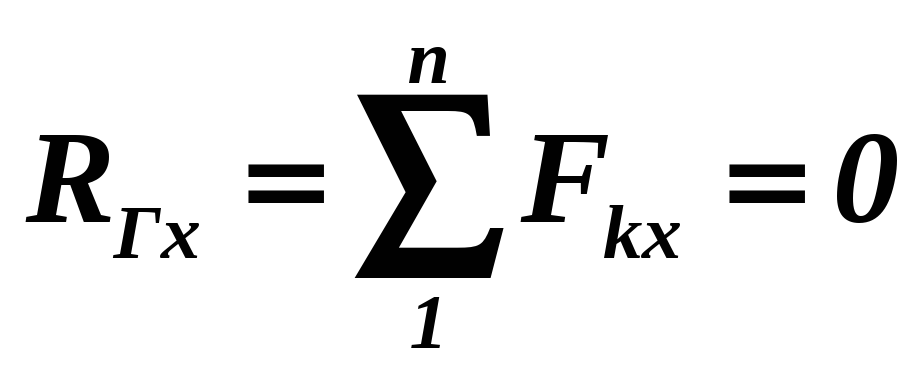 ,
4.
,
4.
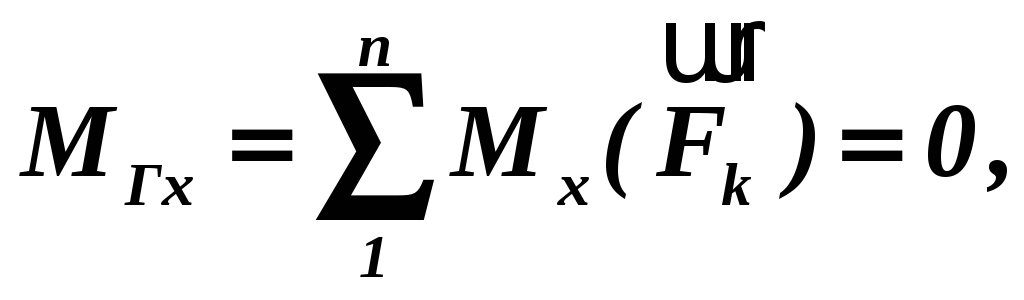
2.
 5.
5.
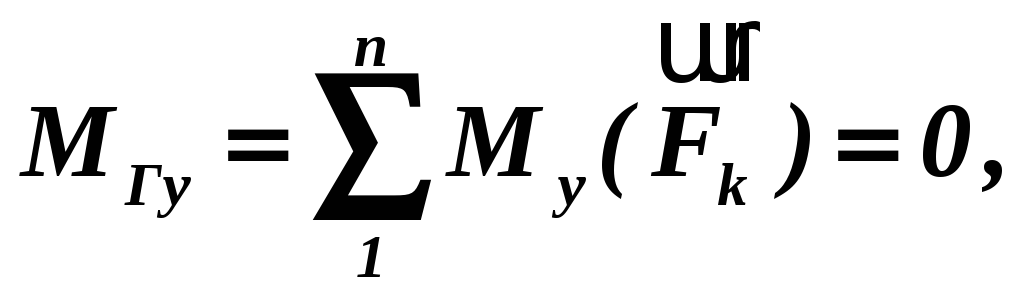
3.
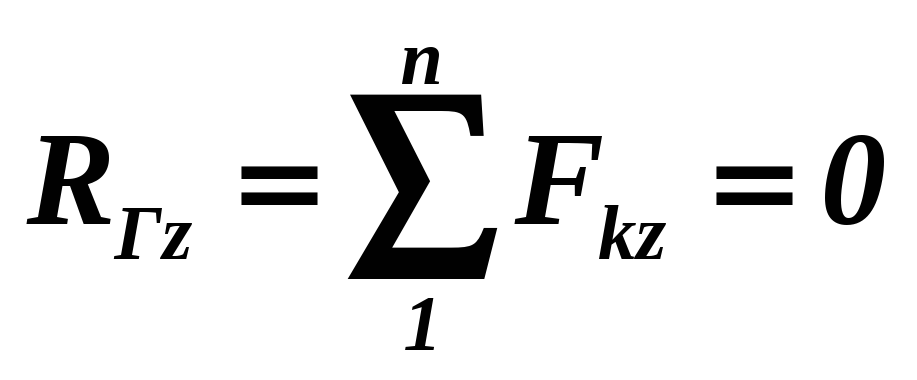 6.
6.
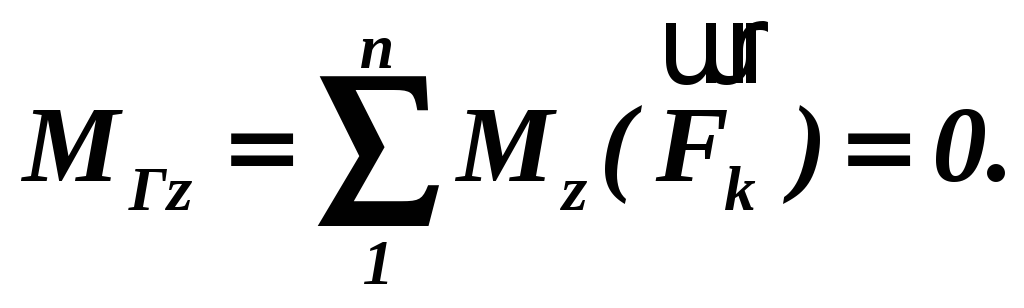
(1.16)
Таким чином, для рівноваги довільної просторової системи сил необхідно і досить, щоб алгебраїчні суми проекцій всіх сил на координатні осі, а також алгебраїчні суми моментів цих сил відносно координатних осей були рівними нулю.
1.9. Окремі випадки рівноваги систем сил
1.9.1. Умови рівноваги просторової системи паралельних сил
Р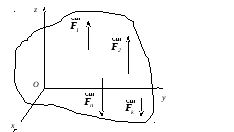 озглянемо
систему сил
озглянемо
систему сил
![]() ,
паралельних осі Oz
(рис.1.17). Очевидно, що в такому випадку
перше і друге рівняння загальних умов
рівноваги довільної просторової системи
сил (рівняння 1.16) перетворюється на
тотожності:
,
паралельних осі Oz
(рис.1.17). Очевидно, що в такому випадку
перше і друге рівняння загальних умов
рівноваги довільної просторової системи
сил (рівняння 1.16) перетворюється на
тотожності:
Рис. 1.17
![]() ,
,
![]() .
.
Крім того, тотожно буде дорівнювати
нулю і останнє (шосте) рівняння умов
рівноваги:
![]() .
Таким чином, умови рівноваги просторової
системи паралельних сил відповідають
рівнянням:
.
Таким чином, умови рівноваги просторової
системи паралельних сил відповідають
рівнянням:
-
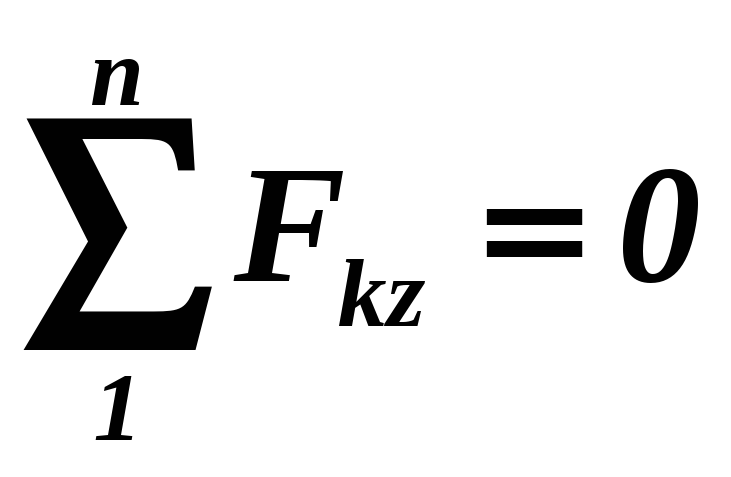 ;
;
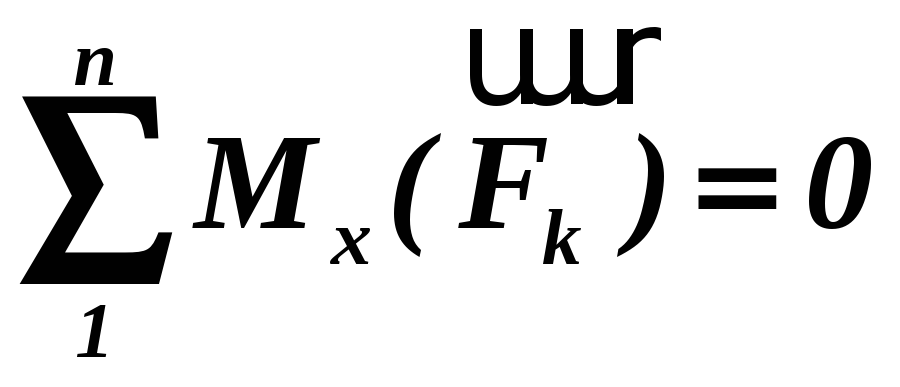 ;
;
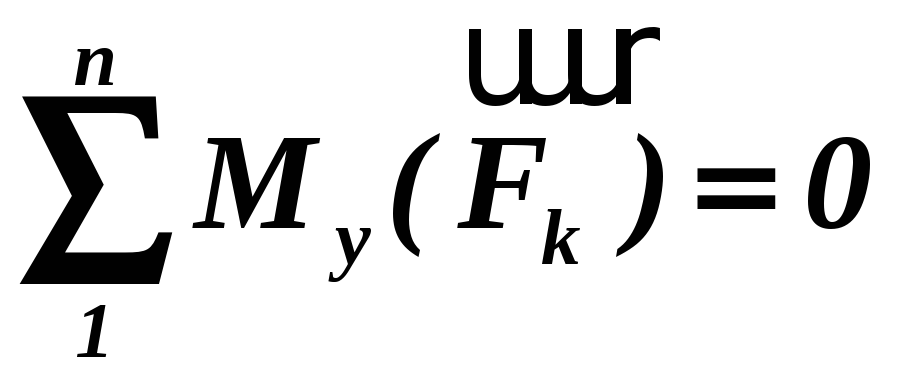
(1.17)
Тобто, для рівноваги просторової системи паралельних сил, прикладених до твердого тіла, необхідно й досить, щоб алгебраїчна сума проекцій всіх сил на вісь, паралельну лініям дії даних сил, дорівнювала нулю і алгебраїчні моменти цих сил відносно двох інших координатних осей також були рівними нулю.
