
- •1. Загальні вимоги по охороні праці
- •1.2 Вимоги безпеки під час роботи
- •1.3 Вимоги безпеки в аварійних ситуаціях
- •1.4 Вимоги безпеки по завершенню роботи
- •2. Похибки вимірювання фізичних величин
- •2.1 Види вимірювань. Похибки.
- •2.2 Обробка результатів прямих та непрямих вимірювань
- •Лабораторна робота №1 Вивчення кінематики і динаміки поступального руху на машині Атвуда
- •Теоретичні відомості і опис установки
- •Хід роботи
- •Хід роботи
- •Хід роботи
- •Хід роботи
- •Контрольні запитання
- •Лабораторна робота № 5 Визначення електроємності конденсатора балістичним гальванометром
- •Теоретичні відомості і опис установки
- •Хід роботи
- •Хід роботи
- •Хід роботи
- •Контрольні запитання
- •Лабораторна робота № 8 Визначення коефіцієнта поверхневого натягу методом відриву кільця
- •Теоретичні відомості і опис установки
- •Хід роботи
- •Контрольні запитання
Теоретичні відомості і опис установки
Машина Атвуда призначена для вивчення поступального руху тіл. Принцип дії приладу оснований на використанні законів вільного падіння.
П рилад
зображений на рис. 1. Легкий блок вільно
обертається навколо осі, що закріплена
у верхній частині вертикальної стійки.
Через блок перекинута нитка, на кінцях
якої висять тягарці А
і Б
з рівними масами M.
На ці тягарці зверху можна покласти ще
один або декілька тягарців різних мас
(m).
Система тягарців при цьому виходить з
рівноваги і починає рухатись прискорено.
рилад
зображений на рис. 1. Легкий блок вільно
обертається навколо осі, що закріплена
у верхній частині вертикальної стійки.
Через блок перекинута нитка, на кінцях
якої висять тягарці А
і Б
з рівними масами M.
На ці тягарці зверху можна покласти ще
один або декілька тягарців різних мас
(m).
Система тягарців при цьому виходить з
рівноваги і починає рухатись прискорено.
На шкалі секундоміра висвічується час рівномірного руху тягарця між фотодатчиками К1, К2.
Розглянемо спочатку рух тягарця Б. Будемо користуватися нерухомою системою координат, центр якої суміщений з віссю блока.
Вісь Ox направимо вниз. Нехай маса додаткового тягарця, що знаходиться на тягарі Б, рівна m.
На тягарець Б діють дві сили: сила ияжіння (M + m)g і сила натягу правої частини нитки T2. За другим законом Ньютона
![]() , (1)
, (1)
де а – прискорення тягарця Б.
Прискорення тягарця А рівне по абсолютній величині прискоренню тягарця Б і направлене в протилежну сторону (вважаємо, що нитка не розтягується).
Нехай натяг лівого кінця нитки буде T1, тоді
![]() . (2)
. (2)
Якщо знехтувати силою тертя, то
![]() . (3)
. (3)
З рівняння (1-3) маємо
![]() . (4)
. (4)
З (4) видно, що рух в даному випадку рівноприскорений. Тягарці, рухаючись рівноприскорено, пройдуть шлях
![]() , (5)
, (5)
де t1 – час рівноприскореного руху.
В момент проходження тягарцем Б кільця додатковий тягарець знімається і тягарці А і Б, рухаючись рівномірно пройдуть шлях
![]() , (6)
, (6)
де v, t2 – швидкість і час рівномірного руху (час, що вимірюється секундоміром).
Підставляючи a і t1 з (4) і (6) в рівняння (5), отримаємо
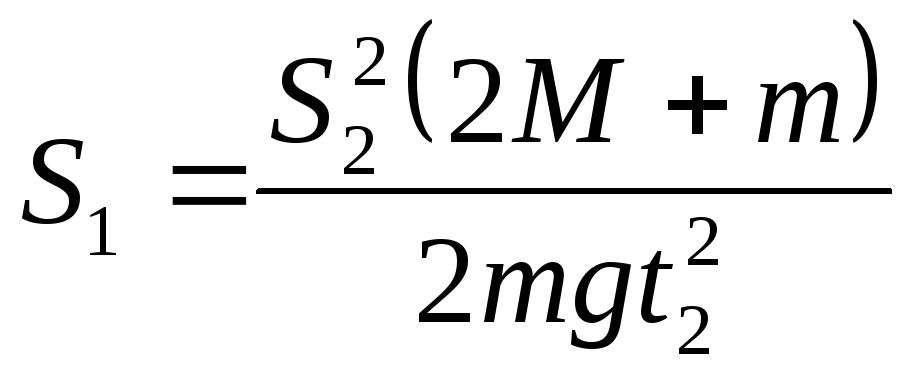
звідки
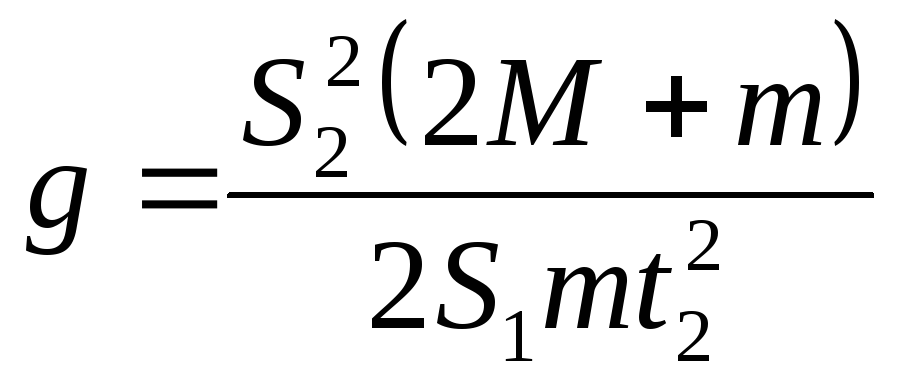 . (7)
. (7)
Хід роботи
-
За допомогою міліметрової шкали на стійці приладу визначити шлях S1 рівноприскореного руху і S2 – шлях рівномірного руху тягарця Б.
-
Записати маси тягарців M і m.
-
Додатковий тягарець покласти на тягарець Б і підняти в верхнє положення.
-
Натиснути кнопку “Сброс” секундоміра, потім натиснути кнопку “Пуск”.
-
Зняти відлік часу t2 рівномірного руху.
-
Дослід повторити не менше трьох разів.
-
Визначити середні значення t2.
-
Оцінити похибку величин.
-
За формулою (7) обчислити прискорення вільного падіння.
-
Оцінити відносну похибку цієї величини за формулою (8).
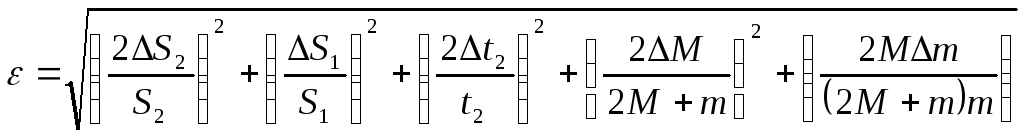
-
Визначити відносну похибку
 за формулою
за формулою
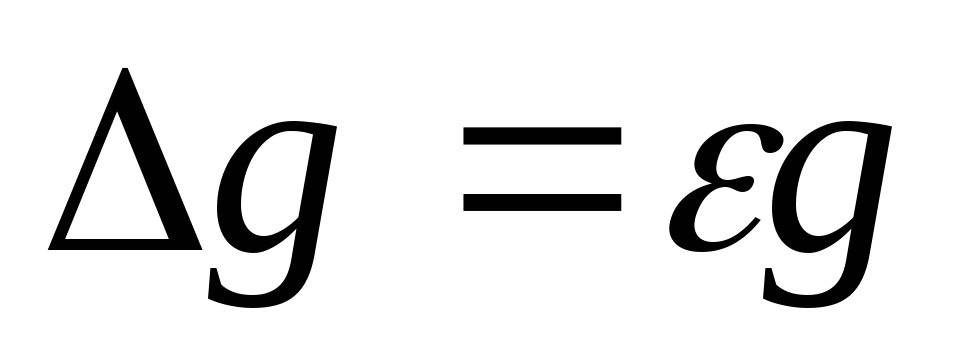 .
Записати кінцевий результат.
.
Записати кінцевий результат.
Таблиця 1
M = , m = , M0 = , m0 = , S0 = , t0 = .
|
№ п.п. |
S1 |
S2 |
t2 |
|
CI |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
Ср. |
|
|
|
Контрольні питання
-
Дати означення векторів миттєвої швидкості і миттєвого прискорення руху тіла.
-
Яка фізична величина називається середньою швидкістю?
-
Який рух називається рівномірним, рівнозмінним?
-
Сформулювати закони Ньютона.
-
Що таке інерціальна і неінерціальна системи відліку?
Лабораторна робота №2
Визначення моменту інерції маятника Максвела
Мета роботи: визначити момент інерції маятника Максвела.
Теоретичні відомості і опис установки
З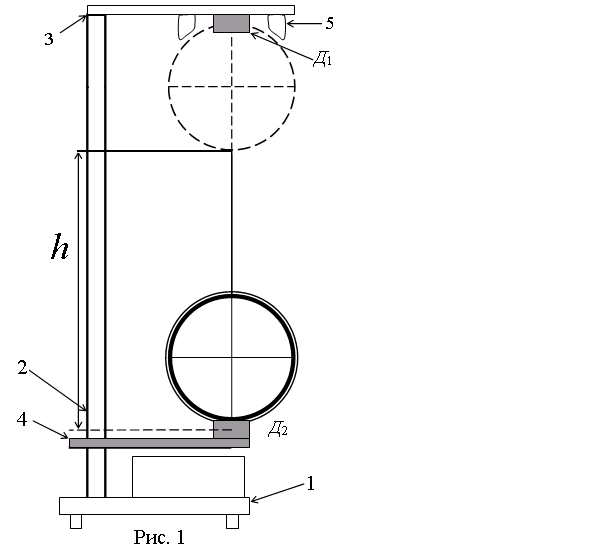 агальний
вигляд маятника Максвела показаний на
рис. 1. На основі 1
закріплена вертикальна стійка 2
до якої прикріплений верхній кронштейн
3
і рухомий нижній кронштейн 4.
На верхньому знаходиться електромагніт
5
і фотоелектричний датчик Д1.
На нижньому кронштейні прикріплений
фотоелектричний датчик Д2.
агальний
вигляд маятника Максвела показаний на
рис. 1. На основі 1
закріплена вертикальна стійка 2
до якої прикріплений верхній кронштейн
3
і рухомий нижній кронштейн 4.
На верхньому знаходиться електромагніт
5
і фотоелектричний датчик Д1.
На нижньому кронштейні прикріплений
фотоелектричний датчик Д2.
Власне маятник – це підвішений біфілярним способом диск, на який одягаються змінні кільця. Таким чином, змінюється момент інерції системи.
Маятник у верхньому положенні утримується електромагнітом. Довжина маятника визначається за допомогою міліметрової шкали, закріпленої на стійці приладу.
Фотоелектричні датчики з’єднані з мілісекундоміром.
Нехай h – віддаль, яку проходить маятник між фотоелектричними датчиками Д1 і Д2. Потенціальна енергія маятника у верхньому положенні
![]() , (1)
, (1)
де m – маса маятника, g – прискорення вільного падіння.
В процесі руху маятника його потенціальна енергія перетворюється у кінетичну. Нехтуючи втратами енергії на роботу проти сил тертя, для кінцевого нижнього положення маятника можна записати закон збереження енергії:
![]() , (2)
, (2)
де v
– швидкість поступального руху маятника
в кінцевому положенні,
– його кутова швидкість в цьому положенні,
I
– момент інерції маятника. У виразі (2)
![]() – кінетична енергія поступального
руху,
– кінетична енергія поступального
руху,
![]() – кінетична енергія обертового руху
системи.
– кінетична енергія обертового руху
системи.
Для рівноприскореного
руху маятника
![]() ,
,
![]() ,
де a
– прискорення, t
– час руху. З останніх співвідношень
маємо
,
де a
– прискорення, t
– час руху. З останніх співвідношень
маємо
![]() . (3)
. (3)
Швидкість поступального руху маятника дорівнює лінійній швидкості точок поверхні осі. Тоді
![]() , (4)
, (4)
де r – радіус осі. З (3) і (4) отримаємо
![]() . (5)
. (5)
Підставляючи (3); (4), (5) в (2) знайдемо момент інерції обертової системи
![]() . (6)
. (6)
Якщо замінити радіус осі через його діаметр d, то
![]() . (7)
. (7)
