§ 2.8. Робота розширення (стискання) газу

Розрахуємо роботу, що виконується газом при зміні його об’єму. Нехай газ поміщений в циліндричну посудину під тісно підігнаним поршнем, що може легко рухатися (рис. 2.6). З боку газу на поршень діє сила тиску F=pS, де р – тиск, S – площа основи поршня. Якщо газ, розширюючись, перемістить поршень на відстань , то він виконає елементарну роботу або . Але – елементарний приріст об’єму газу, тому остаточно

Рис.2.6

. (2.25)

Роботу скінченного приросту об’єму газу від до знаходимо як суму елементарних робіт

. (2.26)

У випадку стискання газу напрямки сили та переміщення поршня протилежні і , . Приріст об’єму тепер теж від’ємний. Таким чином, вирази (2.25) та (2.26) годяться і у випадку стискання газу.

З

Рис.2.7

образимо графічно залежність тиску газу від об’єму у процесі зміни останнього (діаграма p-V, рис.2.7). Виходячи з геометричного змісту інтегралу маємо, що робота газу, розрахована за формулою (2.26), чисельно рівна площі фігури, заштрихованої на рис. 2.7.

Застосуємо тепер вираз (2.26) до ізопроцесів. У випадку ізохорного процесу А=0, бо dV=0. При ізобарному процесі dp=0 і тиск можна винести з-під знаку інтегралу. Тоді маємо

.

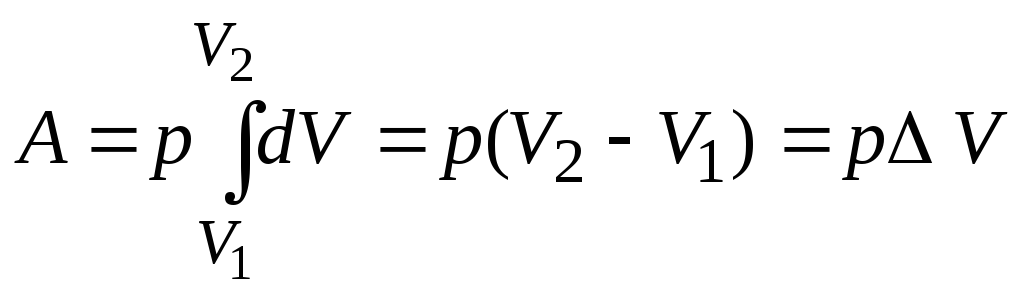Якщо використати рівняння Менделєєва-Клапейрона , то маємо . Тоді робота ізобаричного розширення 1-го моля ідеального газу матиме вигляд . Звідси .

На основі останньої формули маємо фізичний зміст універсальної газової сталої: універсальна газова стала рівна роботі ізобаричного розширення одного моля ідеального газу при нагріванні його на один кельвін.

У випадку ізотермічного процесу dT=0. Тиск у формулу (2.26) підставимо з рівняння Менделєєва-Клапейрона і, винісши сталі величини, виконаємо інтегрування:

.

Остаточно

. (2.27)

Вираз (2.27) можна записати через відношення тисків, якщо скористатися законом Бойля-Маріота :

.

§ 2.9. Перше начало термодинаміки та його застосування до ізопроцесів

В термодинаміці розглядають тільки такі системи, для яких механічна енергія системи як цілого не змінюється. За рахунок виконаної над системою роботи та переданої їй кількості теплоти змінюється лише внутрішня енергія термодинамічної системи :

. (2.28)

Тут – приріст внутрішньої енергії ( та – початкове та кінцеве значення внутрішньої енергії). Співвідношення (2.28) відображає закон збереження і перетворення енергії стосовно теплових процесів.

На відміну від механіки, де частіше приходилося обчислювати роботу зовнішніх сил, в термодинаміці, в основному, мають справу з роботою системи проти зовнішніх сил (А). Саме у зв’язку з цим ці величини тут перепозначені. Перейдемо тепер у рівнянні (2.28) від до ( на основі третього закону Ньютона) і розв’яжемо одержане рівняння відносно Q:

(2.29)

або в диференціальній формі

. (2.30)

– елементарна кількість теплоти, так само як – елементарна робота; – елементарний приріст внутрішньої енергії.

Співвідношення (2.29) (чи (2.30)) є математичним виразом першого начала (закону, принципу) термодинаміки. Формулювання цього принципу: кількість теплоти, наданої системі ззовні, витрачається на роботу системи проти зовнішніх сил і на збільшення внутрішньої енергії системи.

Не треба думати, що завжди за рахунок одержаного тепла внутрішня енергія системи збільшується. Може бути, що ; при цьому на основі (2.29) , тобто система виконує роботу як за рахунок одержаного тепла, так і за рахунок запасу внутрішньої енергії. Як і робота А, так і кількість теплоти Q є величина алгебраїчна: Q<0 означає, що система віддає тепло зовнішньому середовищу (холодильнику), а Q>0 означає, що система одержує тепло від нагрівника. Як і у випадку роботи, для кількості теплоти не можна писати , бо останнє означало б, що значок варіації еквівалентний значку диференціала d, тобто що Q є функцією стану системи. Правильним є запис (сума елементарних кількостей теплоти рівна повній кількості теплоти). Тепер є очевидним, що інтегральна форма запису 1-го принципу термодинаміки (2.29) одержується з диференціальної (2.30), якщо останню проінтегрувати для деякого процесу, початок якого формально позначити “1”, а кінець – “2”:

.

Якісне формулювання 1-го принципу термодинаміки: неможливо побудувати періодично діючий двигун, який виконував би роботу більшу, ніж кількість переданої йому ззовні енергії (вічний двигун І-го роду неможливий).

Тепловий двигун, про який іде мова в якісному формулюванні принципу, це пристрій, що перетворює внутрішню енергію в механічну (“теплоту в роботу”). Основні частини такої установки – робоче тіло (газ, пара), нагрівник і холодильник. Періодично діючий двигун такий, що внаслідок процесу робоче тіло повертається за період до вихідного (початкового) стану; тоді і на основі (2.29).

Застосуємо тепер 1-й принцип термодинаміки до ізопроцесів в ідеальному газі. Оскільки для ізохорного процесу , то з рівняння (2.29) маємо, що . Значить, при ізохорному процесі кількість теплоти, одержана газом ззовні, йде на збільшення внутрішньої енергії газу. При цьому температура газу підвищується (в наступному параграфі буде показано, що внутрішня енергія ідеального газу прямопропорційна абсолютній температурі).

У випадку ізобаричного розширення ідеального газу (див. попередній параграф); оскільки теж додатнє, бо , то на основі (2.29) . Температура газу зростає. 1-й принцип термодинаміки для ізобаричного процесу формулюється як у загальному випадку.

Для ізотермічного процесу робота газу розраховується за формулою (2.27). Оскільки , то і вираз 1-го принципу (2.29) зводиться до наступного: . Це означає, що при ізотермічному процесі кількість теплоти, одержана газом ззовні, йде на роботу газу проти зовнішніх сил.