
- •Глава II Векторная алгебра
- •П. 1 Понятие вектора. Линейные операции
- •Определение 2. Вектор (Гиббс) – математический объект, характеризуемый скалярной величиной, направлением и геометрическим характером сложения.
- •Пример. В одномерном случае преобразование пространства – это биекция, у которой ,.
- •П. 2 Базис на плоскости
- •Доказательство:
- •П. 4 Линейная независимость векторов
- •П. 7 Скалярное произведение векторов
- •Свойства скалярного произведения:
- •Дистрибутивность: .
- •Решение:
- •П. 8 Скалярное произведение в дпск
- •Наличие обратной операции
- •П. 9 Орт вектора. Направляющие косинусы вектора
- •П. 10 Векторное произведение векторов
- •Свойства векторного произведения:
- •Антикоммутативность: .
- •Дистрибутивность:
- •Векторное произведение в дпск
- •Решение:
- •П. 11 Произведения тройки векторов п. 11.1 Смешанное произведение векторов
- •Свойства смешанного произведения
- •Доказательство:
- •П. 12 Основные задачи векторной алгебры
- •П. 12.1 Плоскость в пространстве
- •Основные задачи
- •Угол между двумя плоскостями.
- •Расстояние от точки до плоскости.
- •П. 12.2 Прямая на плоскости
- •Другие уравнения прямой:
- •Угол между двумя прямыми
- •Условие перпендикулярности:
- •Условие параллельности:
- •Расстояние от точки до прямой
- •П. 12.3 Прямая в пространстве
- •Угол между прямыми
- •П.13 Линии второго порядка п.13.1 Эллипс
- •Свойства эллипса
- •Доказательство:
- •П. 13.2 Гипербола
- •Свойства гиперболы
- •П. 13.3 о гиперболических функциях
- •П. 13.4 Парабола
- •Свойства параболы
- •П.14 Поверхности второго порядка п. 14.1 Поверхности вращения
- •П. 14.2 Поверхности второго порядка
- •3. Двуполостной гиперболоид:
- •Цилиндрические поверхности
- •9. Гиперболический параболоид
П. 12 Основные задачи векторной алгебры
Определение 1. Геометрическим местом точек (ГМТ) на плоскости или в пространстве называется множество точек, обладающих заданным свойством, причём никакие другие точки этим свойством не обладают.
Определение 2.
Уравнение
![]() называется уравнением
соответствующего ГМТ относительно
заданной
системы координат,
если при подстановке координат точек
в уравнение ГМТ получается верное
равенство.
называется уравнением
соответствующего ГМТ относительно
заданной
системы координат,
если при подстановке координат точек
в уравнение ГМТ получается верное
равенство.
П. 12.1 Плоскость в пространстве
Характеристика:
Л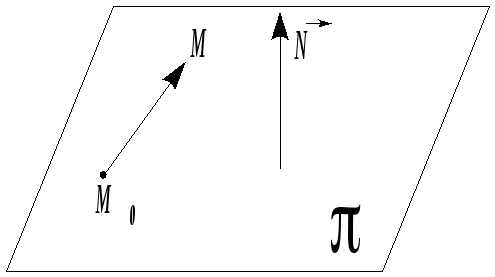 юбая
плоскость задаётся своей нормалью
юбая
плоскость задаётся своей нормалью
![]() (вектором, ортогональным данной плоскости)
и точкой
(вектором, ортогональным данной плоскости)
и точкой
![]() ,
лежащей на этой плоскости.
,
лежащей на этой плоскости.
Базовая задача:
Возьмём произвольную
точку
![]() .
Вектор
.
Вектор
![]() лежит на плоскости
лежит на плоскости
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() .
Раскрывая скобки, получим
.
Раскрывая скобки, получим
![]() .
Обозначим
.
Обозначим
![]() .
Тогда уравнение
.
Тогда уравнение
![]() называют общим
уравнением плоскости.
называют общим
уравнением плоскости.
Существуют и другие уравнения плоскости:
-
Уравнение плоскости в векторной форме:
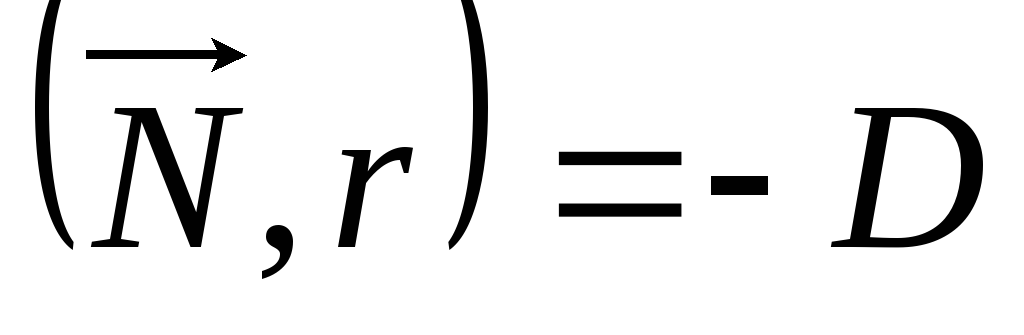 ,
где
,
где
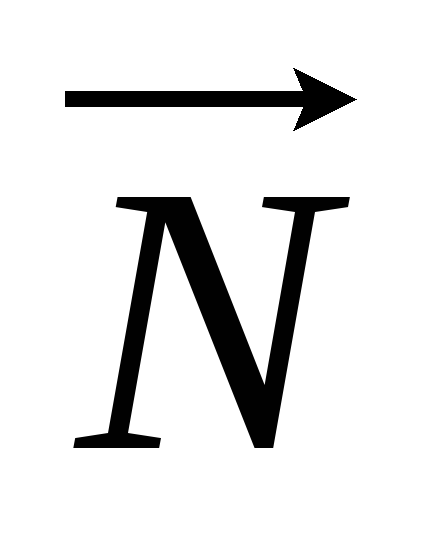 –
нормальный вектор данной плоскости,
–
нормальный вектор данной плоскости,
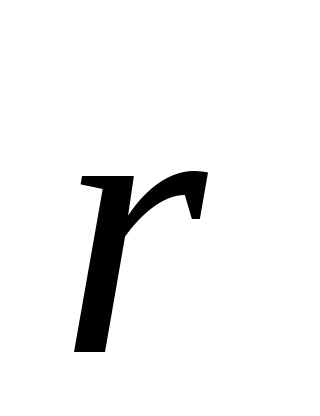 –
радиус-вектор точки
–
радиус-вектор точки
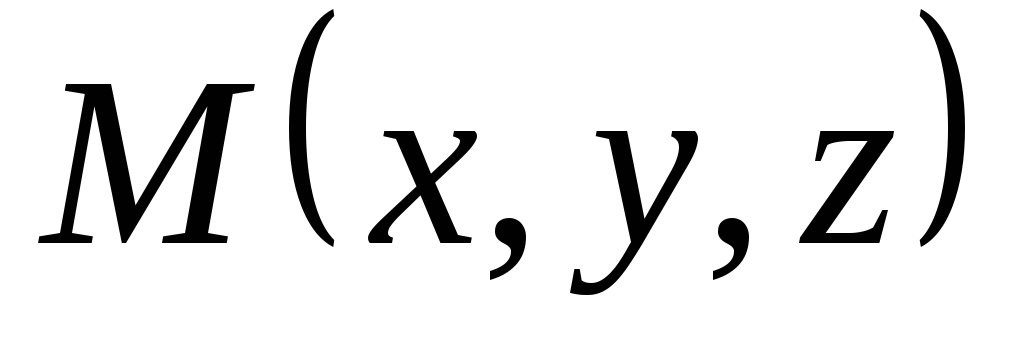 .
.
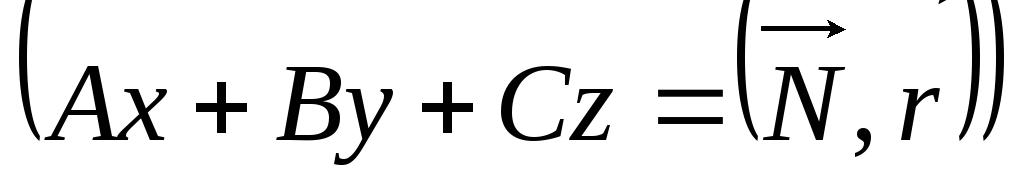
-
Нормальное уравнение плоскости. Так как
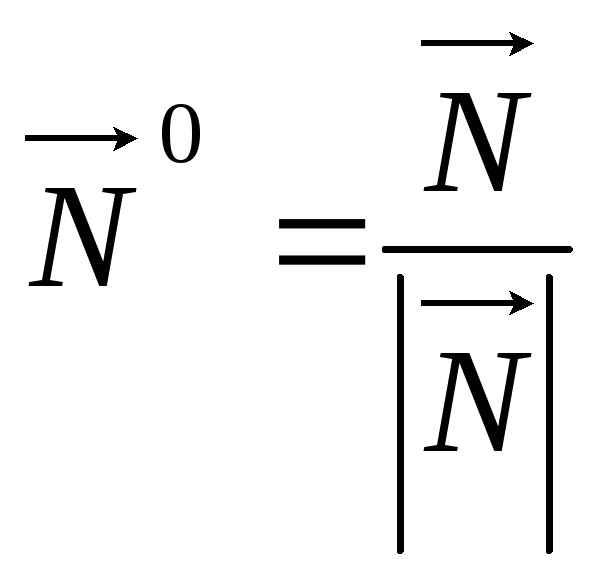 ,
то
,
то
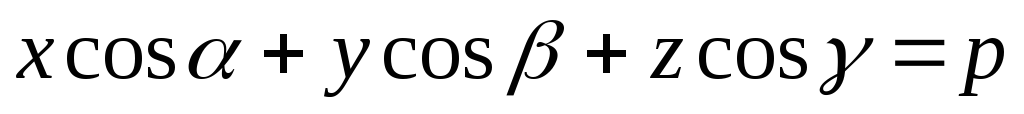 ,
где:
,
где:
 –
направляющие косинусы нормального
вектора
–
направляющие косинусы нормального
вектора
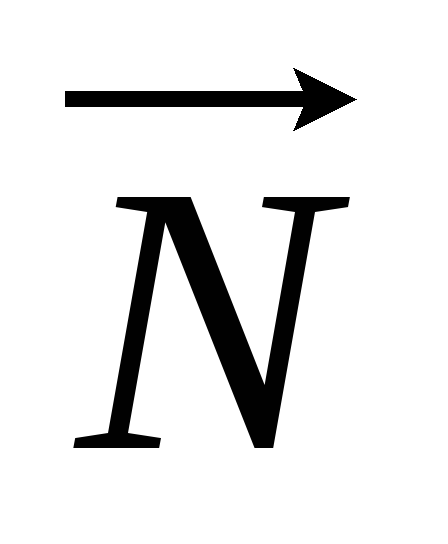 ,
направленного из начала координат в
сторону плоскости;
,
направленного из начала координат в
сторону плоскости;
![]() – расстояние от
начала координат до плоскости.
– расстояние от
начала координат до плоскости.
Нормальное уравнение
плоскости получается путём умножения
общего уравнения на нормирующий множитель
![]() ,
где
,
где
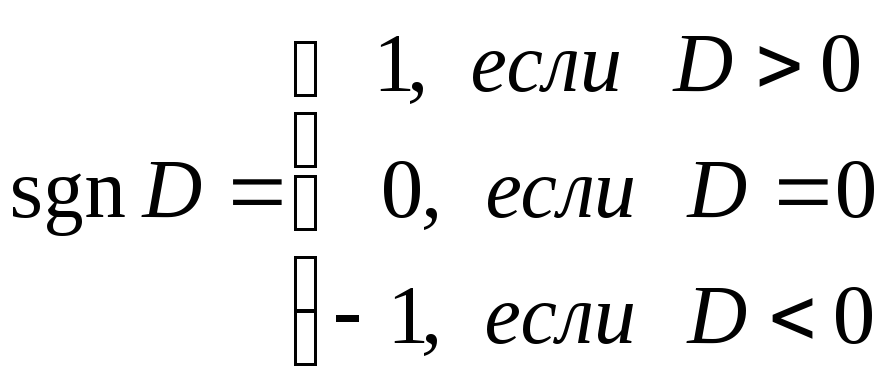 ,
(signum -
знак).
,
(signum -
знак).
-
Уравнение плоскости в отрезках:
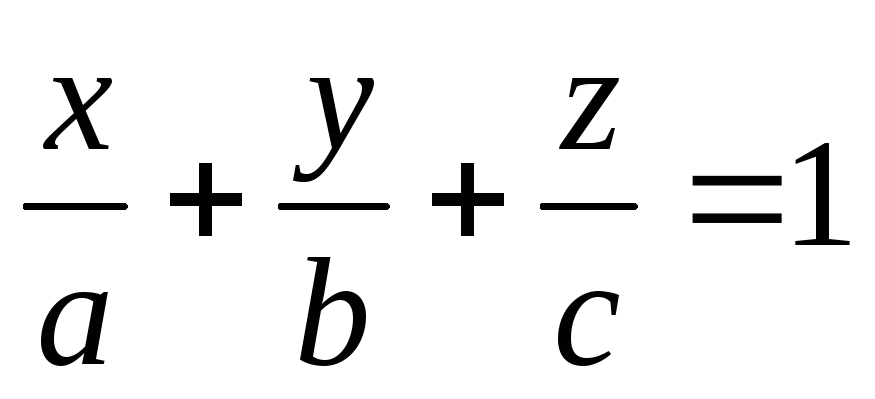 ,
где
,
где
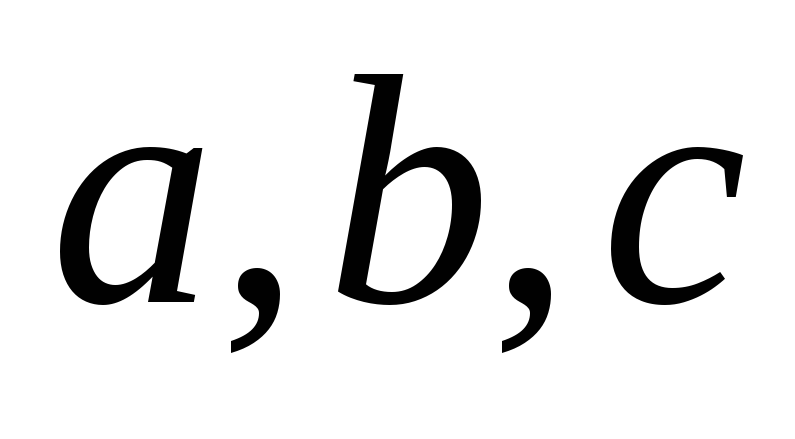 –
величины отрезков, которые отсекает
плоскость на осях
–
величины отрезков, которые отсекает
плоскость на осях
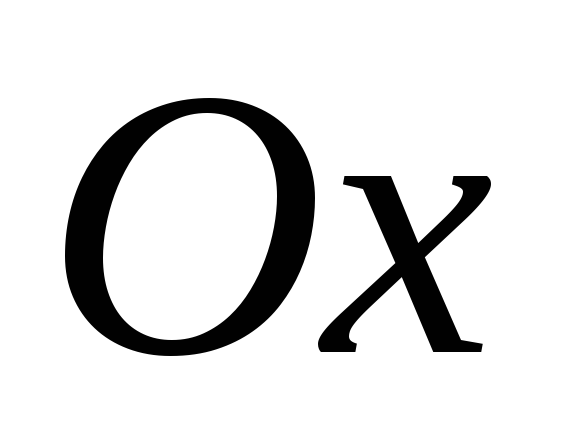 ,
,
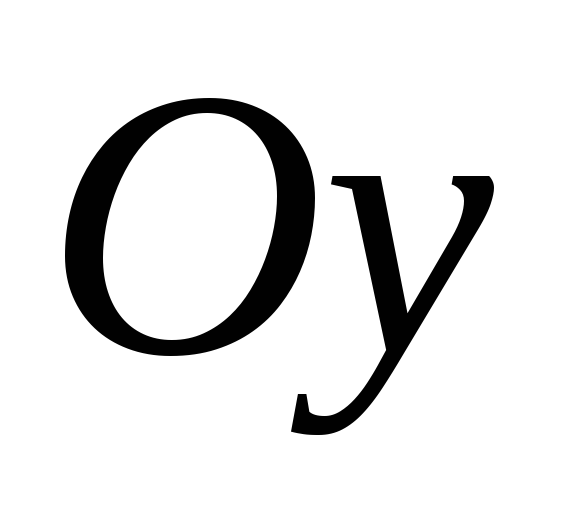 ,
,
 соответственно.
соответственно.
Основные задачи
-
Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой.
Пусть точки
![]() ,
,
![]() ,
,
![]() разл
разл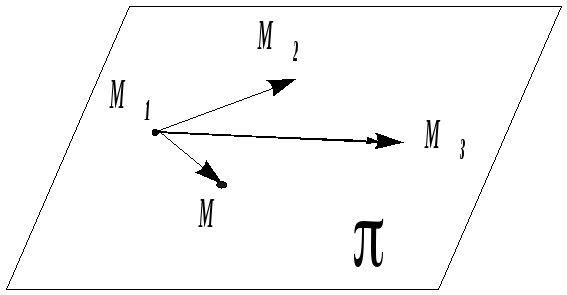 ичные
и не лежат на одной прямой. Выберем
произвольную точку
ичные
и не лежат на одной прямой. Выберем
произвольную точку
![]() так, чтобы три вектора
так, чтобы три вектора
![]() были компланарны. Используем критерий
компланарности трёх векторов. Тогда
уравнение
были компланарны. Используем критерий
компланарности трёх векторов. Тогда
уравнение
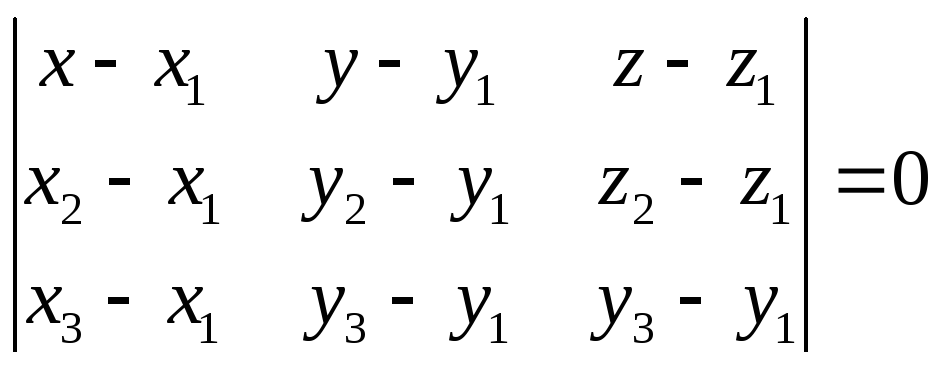 является уравнением искомой плоскости
является уравнением искомой плоскости
![]() .
.
-
Угол между двумя плоскостями.
Определение 1.
Пусть две плоскости
![]() и
и
![]() заданы общими уравнениями
заданы общими уравнениями
![]() и
и
![]() .
Под углом
между двумя плоскостями
.
Под углом
между двумя плоскостями
![]() и
и
![]() будем понимать угол между нормалями к
этим плоскостям. Тогда:
будем понимать угол между нормалями к
этим плоскостям. Тогда:
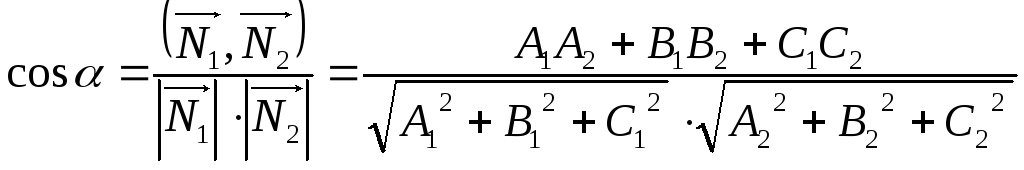 .
.
Условие
перпендикулярности плоскостей
![]() и
и
![]() :
:
![]() .
.
Условие параллельности
плоскостей
![]() и
и
![]() :
:
![]() коллинеарные, т.е.
коллинеарные, т.е.
![]() .
.
-
Расстояние от точки до плоскости.
Если плоскость
![]() задана нормальным уравнением
задана нормальным уравнением
![]() ,
то отклонением
точки
,
то отклонением
точки
![]() от плоскости
от плоскости
![]() называют
называют
![]() .
Знак
.
Знак
![]() указывает на взаимное расположение
точки
указывает на взаимное расположение
точки
![]() на плоскости
на плоскости
![]() и начала координат, а именно:
и начала координат, а именно:
а) если точка
![]() и начало координат лежат по разные
стороны от плоскости
и начало координат лежат по разные
стороны от плоскости
![]() ,
то
,
то
![]() ,
,
б) если
![]() и начало координат находятся по одну
сторону от плоскости
и начало координат находятся по одну
сторону от плоскости
![]() ,
то
,
то
![]() .
.
-
Расстояние
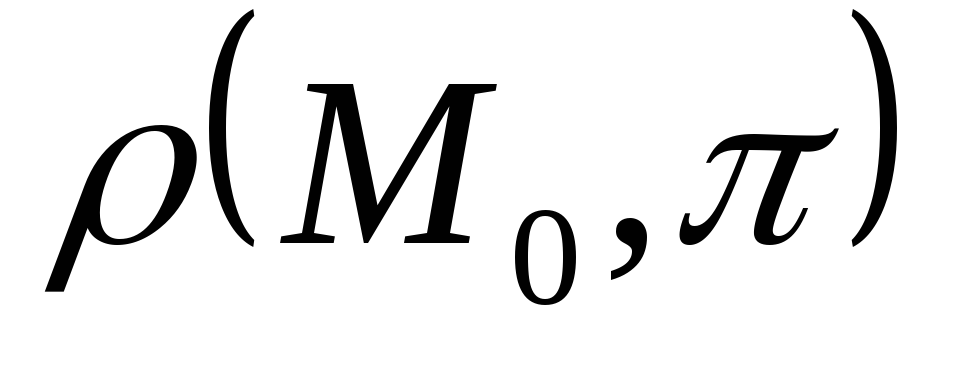 от точки
от точки
 до плоскости
до плоскости
 определяется равенством
определяется равенством
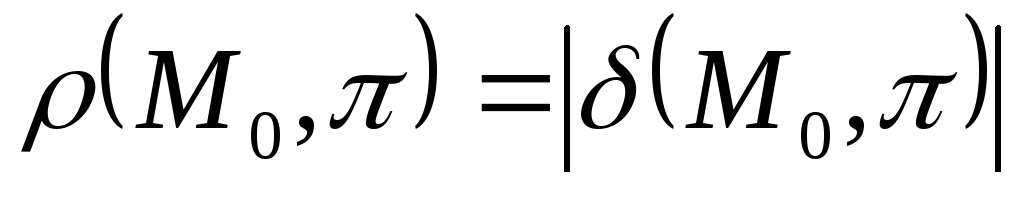 .
.
Итак,
![]() .
.
П. 12.2 Прямая на плоскости
Характеристики:
-
нормальный вектор и точка;
-
направляющий вектор и точка.
Базовые задачи:
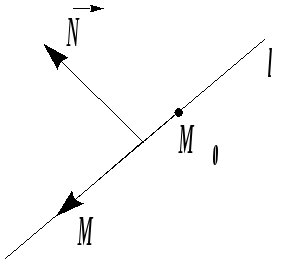
1. Если
на плоскости задана некоторая система
координат, то прямую
![]() можно провести через точку
можно провести через точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]()
 ,
называемого
,
называемого
нормалью
к данной прямой. Тогда, выбрав произвольную
точку
![]() так, чтобы векторы
так, чтобы векторы
![]() и
и
![]() были перпендикулярны, получим уравнение
прямой
были перпендикулярны, получим уравнение
прямой
![]() :
:
![]() ,
,
![]() .
.
Обозначим через
![]() .
Тогда уравнение
.
Тогда уравнение
![]() называется общим
уравнением прямой
называется общим
уравнением прямой
![]() .
.
2.
Проведём прямую
![]() через точку
через точку
![]() параллельно вектору
параллельно вектору
![]() ,
который называют направляющим
вектором
прямой
,
который называют направляющим
вектором
прямой
![]() .
Выберем произвольную точку
.
Выберем произвольную точку
![]()
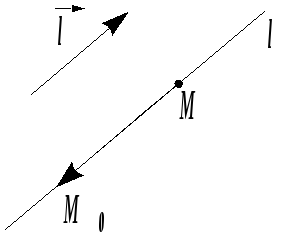 так, чтобы векторы
так, чтобы векторы
![]() и
и
![]() были коллинеарными. Тогда
были коллинеарными. Тогда
![]() – каноническое уравнение прямой.
– каноническое уравнение прямой.
Из последнего
уравнения также можно получить общее
уравнение прямой
![]() ,
заметив, что векторы
,
заметив, что векторы
![]() и
и
![]() перпендикулярны, причём
перпендикулярны, причём
![]() ,
,
![]() .
.
