Глава II Векторная алгебра

Мы не можем ждать милостей от природы,

после того, что мы с ней сделали.

И. Мичурин - Геростратенко.

В IX веке в Багдадском «Доме Мудрости» Мухаммед Аль Хорезми написал «Китаб аль-джебр валь-мукабала» (книга о восстановлении и противопоставлении). Латинизированная транскрипция слова аль-джебр (о восстановлении) и имени автора дала термин «алгебра» и «алгоритм».

П. 1 Понятие вектора. Линейные операции

Замечание. «Вектор» от лат. vehere значит перемещать. Таким образом, вектор и этимологически и созерцательно, это прямолинейный направленный отрезок, результат перемещения точки А в точку В вне зависимости от количества промежуточных точек ,,…

. Это правило сложения векторов называется правилом многоугольника.

Определение 1. Скаляр (от латинского scala – шкала, колонна) – математический объект, характеризуемый величиной и независимостью от выбора начала отсчета.

Пример. 1997 год – это год от Рождества Христова. У иудеев и мусульман точки отсчета другие. Древние китайцы и египтяне вели отсчет с начала династий и т.д. Таким образом, год не является скалярной величиной. Возраст человека не зависит от того, где ему не повезло родиться, т.е. это скаляр.

Определение 2. Вектор (Гиббс) – математический объект, характеризуемый скалярной величиной, направлением и геометрическим характером сложения.

Пример. Ток в цепи постоянного тока обладает величиной, ему приписываетс от греч.я направление. Но это не вектор, так как токи складываются не по правилу многоугольника, а по закону Кирхгофа.

Различают связанные вектора (например, напряженность электромагнитного или гравитационного поля в точке), скользящие вектора, которые не меняются при перемещении вдоль линии своего действия и свободные (геометрические) вектора.

Введем понятие свободного вектора.

Определение 3. Пусть точке геометрического пространства по какому-либо правилу сопоставляется точка того же пространства (точка называется образом точки , а точка – прообразом точки ). Преобразование пространства – это правило такого соответствия между точками и (и его результат), при котором:

1) множество образов и прообразов занимает всё пространство;

2)между точками и установлена биекция, т.е. .

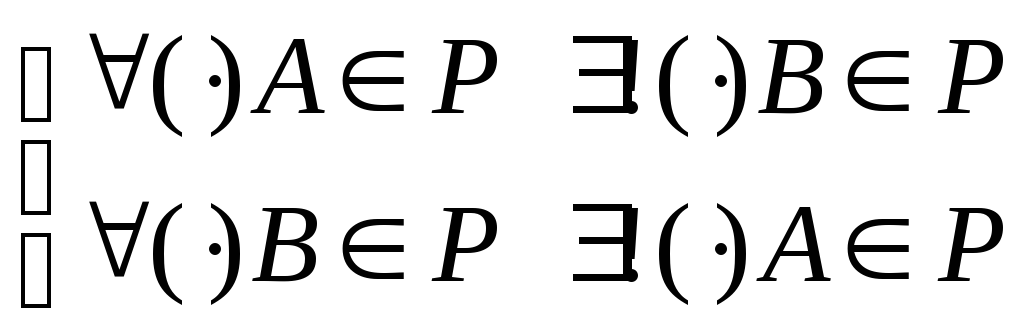Пример. В одномерном случае преобразование пространства – это биекция, у которой ,.

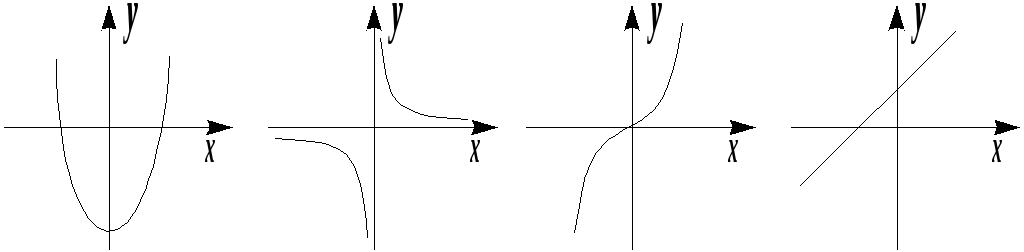
а)	б)	в)	г)
рис. 2.3

На рис. 2.3:

а) и б) – не преобразования пространства; в) и г) – преобразования пространства.

Определение 4. Рассмотрим параллельные лучи и , начинающиеся в точках  и . Они всегда лежат в одной плоскости , которая делится прямой , 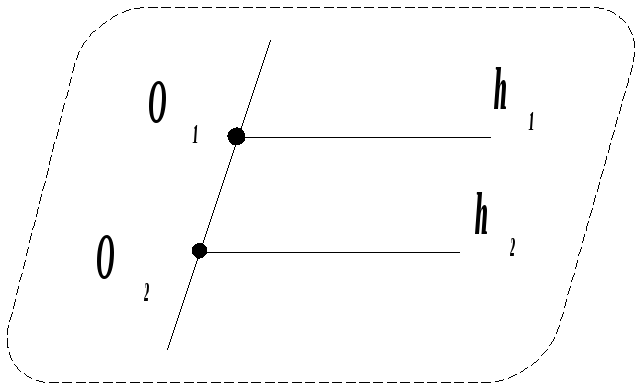проходящей через и , на две полуплоскости. Лучи и называются сонаправленными, если они лежат в одной полуплоскости, и контранаправленными в противном случае (рис. 2.3). В случае, когда и лежат на одной прямой, то они называются сонаправленными, если их пересечение есть луч и контранаправленными - если их пересечение не есть луч (рис. 2.4).

и - сонаправлены.	и - контранаправлены.
рис. 2.5

Определение 5. Вектором называется преобразование пространства , переводящее произвольную точку пространства в точку таким образом, что произвольная точка переходит в точку , точку , причем лучи и сонаправлены, а расстояние между точками и : равно расстоянию между точками и :

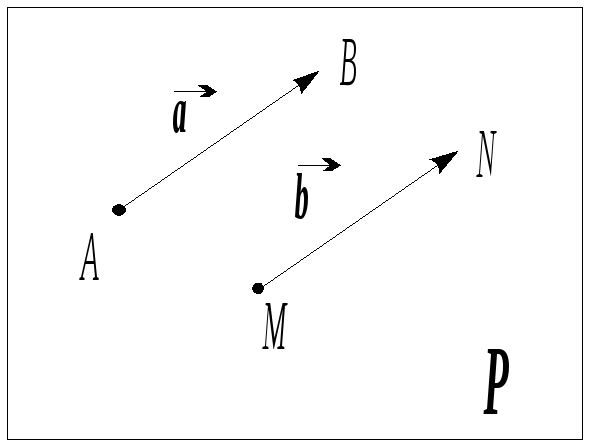, т.е. .

Таким образом, направленный отрезок, о котором шла речь выше, можно рассматривать как модель вектора. Этот отрезок указывает, на какую величину и в каком направлении произошел сдвиг всего пространства.

Как всегда в математике, под вектором понимают не только правило, по которому осуществляется преобразование пространства (рис.2.5), но и его результат. В этом случае удобно говорить о векторе и равному ему векторе , а именно:

Определение 6. Говорят, что вектор равен вектору , если:

1) они лежат на сонаправленных лучах (носителях);

2) .

Определение 7. Сумма векторов определяется, по правилу многоугольника (см. начало пункта), и из него, в частности, следует известное из школы правило параллелограмма для сложения векторов. В частности, суммой векторов и называется вектор, проведенный из начала вектора к концу вектора , если конец вектора и начало вектора совмещены.

Правило многоугольника (в частности, в случае треугольника) и параллелограмма можно проиллюстрировать таким образом:

Определение 8. Под произведением вектора на число , (действительное число, не равное 0) понимается вектор , такой что:

1);

2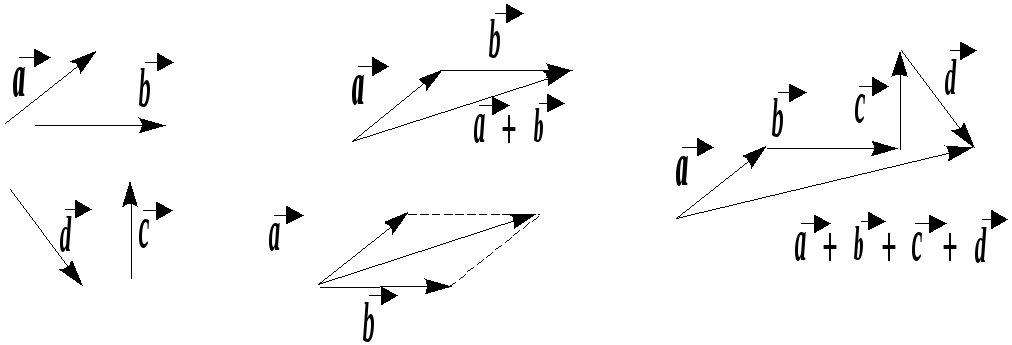) при вектора и лежат на сонаправленных, а при - на контранаправленных лучах.

Определение 9. При вектор называется противоположным вектору .

Определение 10. , называется нуль вектором. Он не имеет направления, что позволяет считать его параллельным любому вектору и, кроме того, нулевой вектор совпадает со своим противоположным. Нуль вектор можно также определить, как произведение вектора на число нуль: .

Определение 11. Под разностью векторов и понимают вектор .

Пример.  Дано: вектор .

Найти: и .

Решение:

Определение 12 Совокупность всех векторов геометрического пространства образует множество, на котором определены операции равенства, сложения, умножения вектора на число, причем:

1) в результате их применения получается вектор из этого же мно­жества;

2) эти операции подчиняются следующим правилам: ,, – векторов и – действительных чисел:

 – коммутативность сложения;

 – ассоциативность сложения;

 – ассоциативность умножения;

 – существование нуль вектора;

 – существование тождественного вектора;

 – связь вектора с противоположным;

 – дистрибутивность относительно сложения векторов;

 – дистрибутивность относительно сложения чисел.

Такое множество называется векторным пространством над множеством действительных чисел.

Позднее мы обобщим понятие вектора и внесем в понятие векторного пространства новое содержание.

Пример.  Дано: – точка пересечения медиан треугольника , О – произвольная точка пространства.

Доказать: .

Доказательство:

Рассмотрим векторы: , , . Найдём . Покажем, что .

Построим параллелограмм . По правилу параллелограмма: . Диагонали параллелограмма, пересекаясь, делятся пополам, следовательно, .

Точка является серединой стороны треугольника, а – его медиана. Медианы треугольника, пересекаясь, делятся в отношении 2:1, считая от вершины, поэтому . Таким образом, , но , следовательно . ■

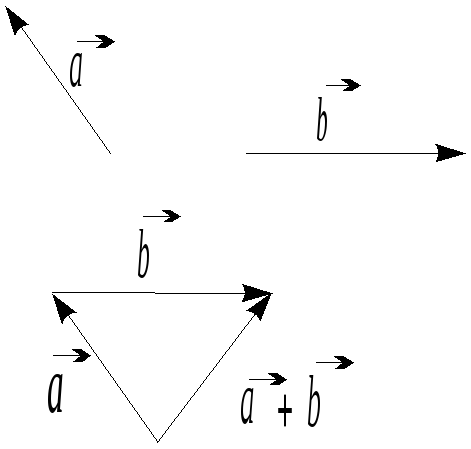
Пример.  Дано: произвольные вектора и .

Доказать:

1. . Равенство имеет место тогда и только тогда, когда ;

2. . Равенство имеет место тогда и только тогда, когда и || ||.

Доказательство:

Если один из векторов или нулевой, то эти неравенства очевидны. Пусть и – ненулевые векторы и пусть направленный отрезок изображает вектор .

Отложим вектор , тогда изображает . Получаем равенство , которое имеет место тогда и только тогда, когда , т.е. векторы и сонаправлены.

Рассмотрим . Следовательно, . Равенство , как доказано выше, имеет место тогда и только тогда, когда векторы и сонправлены, т.е. сонаправлены векторы и , . Отсюда . ■